книги / Нефтегазовая гидромеханика

ВРоссии существует уникальное месторождение – Ярегское, которое разрабатывается термошахтным методом. Месторождение представлено терригенными породами девонской системы. По разрезу вскрыто три пласта, в которых выявлено наличие нефти. Объект разработки, III пласт, залегает на глубине 180–200 м. Свойства

нефти аномальные: вязкость дегазированной нефти при пластовой температуре достигает 15–20 МПа·с, газовый фактор 10 м3/т. Эта нефть обладает вязкоупругими свойствами. С 1939 г. месторождение разрабатывается шахтным методом. До 1953 г. пласт разбуривался плотной сеткой вертикальных и наклонных скважин из выработок, расположенных на 20–30 м выше кровли продуктивного пласта. Забои размещались по треугольной сетке на расстоянии 12–25 м друг от друга. При этом КИН составил всего 4,4 %. Далее была реализована другая система разработки. В 1968 г. в пласт начата закачка пара. Двухгоризонтная система разработки: пар давлением 1–2 атм закачивается через скважины надпластового горизонта, а нефть отбирают через пологовосходящие скважины, пробуренные под разными углами к горизонту. При этом достигался равномерный прогрев пласта и максимальное использование гравитационного режима.

На Ухтинском нефтеперерабатывающем заводе из ярегской нефти получают мазут, прекрасные по качеству дорожные и строительные битумы, а также исключительно хорошие лаковые битумы, морозостойкие смазочные масла и зимнее дизтопливо.

2.13.Установившееся нерадиальное движение несжимаемой жидкости при линейном законе фильтрации

Вотличие от плоскорадиального движения жидкости, при котором линии тока прямолинейные и скорость фильтрации жидкости

впотоке зависит лишь от расстояния живого сечения от центра потока, при нерадиальном движении жидкости линии тока всегда криволинейные (что не позволяет уподобить движение жидкости одномерному потоку). В нерадиальных потоках конфигурация линий тока и величины расходов жидкости в различных областях течения жидкости неодинаковы и зависят от формы контура питания, распо-

131

ложения источников и стоков и величин давления на забоях скважин. По этой причине без особого труда можно получить лишь частные решения дифференциального уравнения движения жидкости для ограниченного числа практических задач. Суть подхода к решению задач сводится к тому, что фильтрационное поле, соответствующее нерадиальному потоку жидкости, рассматривается как результат суммирования взаимодействующих полей. Если в бесконечном пласте имеется некоторое количество произвольно расположенных источников и стоков, то каждый такой источник или сток образует вокруг себя фильтрационное поле, а в силу того, что сами источники и стоки взаимодействуют (интерферируют) друг с другом, то все точки пространства, занятого движущейся жидкостью, одновременно находятся в фильтрационных полях, образуемых всеми скважинами, т.е. одновременно испытывают влияния всех скважин. Следовательно, потенциал в любой точке поля, образованного целой системой взаимодействующих скважин, равен алгебраической сумме потенциалов полей (в соответствующих точках), образованных каждой из скважин всей группы.

i=1

где Фi – потенциал i-го поля в некоторой точке; n – количество по-

лей, соответствующее числу взаимодействующих скважин.

Этот принцип получил название принципа суперпозиции и широко применяется для решения практических задач.

Движение жидкости от нагнетательной скважины к экс-

плуатационной. Пусть в однородном горизонтальном бесконечном пласте постоянной толщины пущены в эксплуатацию две равнодебитные скважины: эксплуатационная А и нагнетательная В (рис. 2.47). Скважины имеют одинаковый радиус rс. В пласте происходит установившееся движение несжимаемой жидкости по линейному закону фильтрации. Расстояние между скважинами 2σ; r1, r2 – радиус-векторы, проведенные из центров скважин в любую точку пласта М.

132

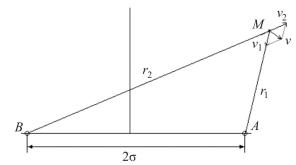
Рис. 2.47. Схема эксплуатационной А и нагнетательной В скважин

Предположим, что в пласте работает единственная эксплуатационная скважина А. Скорость фильтрации v1 в любой точке пласта будет направлена по радиусу к центру скважины; по величине скорость фильтрации будет обратно пропорциональна расстоянию до центра скважины.

Допустим, что в том же пласте работает единственная нагнетательная скважина В, а эксплуатационная бездействует. Вектор скорости фильтрации v2 направлен по радиусу от центра скважины.

Если скважины А и В работают одновременно, то результирующий фильтрационный поток можно получить путем наложения (суперпозиции) двух потоков. Вектор скорости результирующего потока v строится по правилу параллелограмма.

На рис. 2.48 изображены траектории движения жидкости к скважине А и от скважины В. Дуги окружностей, полученные пересечением этих линий, являются траекториями движения жидкости от нагнетательной скважины к эксплуатационной.

На рис. 2.49 выполнено графическое наложение двух потоков в предположении равной дебитности нагнетательной и эксплуатационной скважин. Итак, системой траекторий является семейство окружностей, проходящих через центры скважин; центры круговых траекторий лежат на прямой, перпендикулярной линии центров скважин и делящей расстояние между ними пополам. Линии, пер-

133

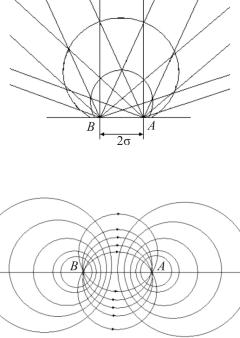
пендикулярные траекториям, являются изобарами. Изобарами рассматриваемого фильтрационного потока будут окружности, эксцентричные скважине.

Рис. 2.48. Графическое наложение фильтрационных потоков эксплуатационной и нагнетательной скважин

Рис. 2.49. Траектории и изобары в потоке жидкости от нагнетательной скважины к эксплуатационной

Семейства траекторий и изобар получились бы гораздо сложнее, если бы скважины были разнодебитными.

Поскольку разность забойных давлений между нагнетательной и эксплуатационной скважинами в данном случае является единственным источником для движения жидкости (никакого другого контура питания в пласте нет), необходимым условием для существования установившегося движения жидкости в пласте является:

134

Здесь, как и ранее, знак «минус» приписывается приемистости нагнетательной скважины. Скважины, образующие своеобразный гидродинамический диполь, расположены друг от друга на расстоянии 2σ в бесконечном изотропном пласте. Произвольно выберем одну из точек пространства М. Будем считать, что выбранная точка находится в фильтрационном поле, образованном нагнетательной скважиной на расстоянии r1 от нее. Тогда вектор скорости фильтра-

ции в данной точке поля ν1 будет направлен по радиус-вектору

в сторону о нагнетательной скважины. Когда эта же точка будет находиться в фильтрационном поле эксплуатационной скважины (расстояние от точки до скважин r2 ), то вектор скорости фильтрации

в данной точке ν2 будет направлен по радиус-вектору в сторону

эксплуатационной скважины. Модули векторов будут обратно пропорциональны расстоянию до соответствующих скважин. Поскольку точка находится одновременно в поле двух скважин, то вектор ско-

рости фильтрации в точке будет равен сумме векторов (νM =

= ν1 + ν2 ). В следующий момент времени частица жидкости пере-

местится из точки М в соседнюю точку N, в которой составляющие вектора ее скорости изменятся, поскольку частица жидкости будет удаляться от нагнетательной и приближаться к эксплуатационной скважине и, таким образом, будет смещаться в горизонтальном направлении (в сторону эксплуатационной скважины).

Точки М и N – лишь промежуточные точки криволинейной траектории частицы жидкости: эта траектория начинается на забое нагнетательной скважины и заканчивается на забое эксплуатационной скважины. Аналогичные пути проделывают и остальные частицы жидкости, двигающиеся от забоя нагнетательной скважины к забою эксплуатационной. Фильтрационный поток графически можно представить в виде совокупности криволинейных траекторий частиц жидкости (линий тока).

Давление в точке М в фильтрационном поле нагнетательной скважины определится следующим образом:

135

Давление в той же точке в поле эксплуатационной скважины:

Согласно принципу суперпозиции давление в точке, расположенной одновременно в фильтрационном поле сразу двух скважин,

Анализируя полученное уравнение, можно отметить, что во всех точках, в которых выполняется условие

давления одинаковы, т.е. это уравнение линии соединяющей точки пространства, в которых давления одинаковы (уравнение изобары). Таким образом, карта изобар потока представляет собой семейство неконцентрических окружностей, центры которых смещаются во внешнюю сторону по отношению к паре работающих скважин. По мере смещения центров изобар они сгущаются внутрь диполя и имеют разрежение во внешней области диполя. Через середину отрезка, соединяющего скважины в перпендикулярном направлении, будет проходить центральная изобара, соответствующая пластовому давлению.

Чтобы определить расход жидкости в потоке (в том числе дебит эксплуатационной и приемистость нагнетательной скважин), необходимо подставить в единое уравнение забойные давления в скважинах с расходом. Для точки на забое нагнетательной скважины: r1 = rс и r2 ≈ 2σ; для точки на забое эксплуатационной скважины:

r2 = rс и r1 ≈ 2σ. Тогда забойное давление в нагнетательной скважине определяется как

136

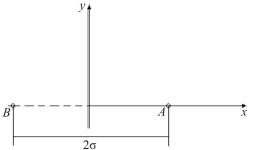
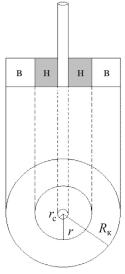
Приток жидкости в скважину при прямолинейном контуре питания. Задача сводится к рассмотренному потоку жидкости от нагнетательной скважины к эксплуатационной (рис. 2.50). Заметим, что прямолинейный контур питания можно рассматривать как центральную изобару в гидродинамическом диполе, если симметрично от контура питания (по другую его сторону) расположить фиктивную нагнетательную скважину, с помощью которой и будет образована центральная изобара, эквивалентная прямолинейному контуру питания. Дебит такой скважины

где Lк – расстояние от контура питания до скважины. Аналогичным образом может быть решена еще одна частная

задача о токе жидкости к скважине, эксцентрично расположенной по отношению к круговому контуру питания. В данном слу-

чае круговой контур питания может рассматриваться как одна из изобар потока между нагнетательной и эксплуатационной скважинами, т.е. этот контур питания также может быть заменен фиктивной нагнетательной скважиной. Дебит такой скважины

137

гдеd – расстояниеотскважиныотцентракруговогоконтурапитания. При большем количестве скважин формулы для определения дебитов скважин усложняются, а для более сложных систем получить необходимые зависимости становится практически невозможно. В таких случаях можно воспользоваться приближенными ме-

тодами.

Рис. 2.50. Схема расположения скважин при нерадиальном движении жидкости в пласте с прямолинейным контуром питания

Движение границы двух сред. При разработке нефтяных ме-

сторождений при режимах вытеснения, например при водонапорном, происходит стягивание контура нефтеносности под действием напора воды. Задача продвижения водонефтяного контакта является одной из наиболее сложных в теории фильтрации.

В залежах пластового типа перемещение водонефтяного контакта в основном горизонтальное, в массивных залежах – вертикальное.

Перемещение ВНК описывают с помощью двух моделей – поршневого и непоршневого вытеснения.

Поршневое вытеснение нефти водой. В общем случае на гра-

нице раздела двух жидкостей с различными физическими свойства-

138

ми происходит преломление линий тока. Учет этого преломления

исоставляет главную трудность в точном решении задачи о вытеснении нефти водой. Линии тока не преломляются при одномерном

ирадиальном движениях, когда в начальный момент времени они перпендикулярны границе раздела. В этих случаях получены точные решения, в которых жидкости принимаются несжимаемыми, пласт – горизонтальным, режим пласта – водонапорным, фильтрация – происходящей по линейному закону.

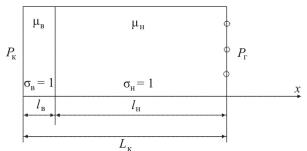
Вытеснение нефти водой в полосообразной залежи. Поршне-

вое вытеснение: учитывается различие в вязкости нефти и воды, а плотности считаются одинаковыми, что дает возможность рассматривать границу раздела вертикальной. Постепенно фронт вытеснения будет занимать последовательные положения (рис. 2.51).

Рис. 2.51. Вытеснение нефти водой в полосообразной залежи

Из приведенной формулы видно, что дебит нефти при заданных постоянных значениях Рк и Рг возрастает при продвижении границы раздела, если вязкость нефти больше вязкости воды.

Распределение давления в нефте- и водонасыщенной частях залежи определится по формуле

Величина давления в некоторой точке пласта при вытеснении нефти водой зависит не только от ее координаты, но и от положения фронта вытеснения, которое, в свою очередь, зависит от времени. Даже при постоянстве давлений на контуре питания и в скважине процесс вытеснения нефти водой представляет собой неустановившуюся фильтрацию.

Поэтому все дифференциальные уравнения для процесса вытеснения нефти водой записываются через частные производные.

Время вытеснения нефти водой определяется по формуле

Схема вытеснения нефти водой в круговой залежи представлена на рис. 2.52.

Рис. 2.53. Вытеснение нефти водой в круговой залежи

140