книги / Теория линейных электрических цепей. Ч. 1

контуров и источников. С усложнением электрических цепей такой расчет становится крайне затруднительным, в связи с чем требуется применение метода, позволяющего рассчитывать электрические цепи переменного тока аналогично цепям постоянного тока. Таким удобным расчетным методом служит символический метод.

3.3.Символический метод расчета цепей с гармоническими воздействиями

Расчет цепей периодического синусоидального тока облегчается, если поставить в соответствие синусоидальной функции комплексное число или вектор. Установим данное соответствие.

Пусть некоторая электрическая величина (ток, напряжение, ЭДС и т.д.) изменяется по синусоидальному закону

v = Vm sin(ω t + ψ ) .

В прямоугольной системе координат (рис. 3.12) расположим

Представим себе, что вектор с момента t = 0 начинает вращаться вокруг начала

координат в положительном направлении с постоянной угловой скоростью, равной угловой частоте ω . В момент времени t ≠ 0 вектор составляет с осью абсцисс угол ω t + ψ . А его проекция на ось ординат

V y = Vm sin(ω t + ψ ) будет равна мгновенному значению величины v.

Таким образом, между мгновенным значением v(t) и вектором V можно установить однозначное соответствие. На этом основании век-

тор V будем называть вектором, изображающим функцию времени, и

101

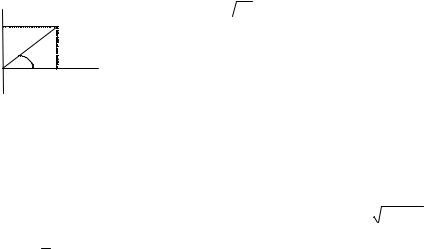
обозначать V . Эти векторы являются математической абстракцией, не имеющей физического смысла, а служат исключительно для удобства расчетов. Поэтому такие изображения функции времени называют

символическими.

Если считать ось абсцисс осью вещественных величин, а ось ординат – осью мнимых величин на комплексной плоскости, то полученный вектор соответствует комплексному числу V с модулем Vm и

аргументом ψ . Это комплексное число называют комплексной амплитудой. Иначе говоря, это комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно амплитуде и начальной фазе заданной синусоидальной функции.

3.3.1. Понятие о комплексных числах

ϕ = arctg b . a

Переход от показательной формы к тригонометрической выполняется при помощи формулы Эйлера: A = Ae jϕ = Acos ϕ + jAsin ϕ .

102

означает поворот на угол ψ i в комплексной плоскости; e jω t называют фактором вращения, умножение на который означает вращение вектора с постоянной частотой ω в положительном направлении вокруг начала координат.

В этой связи следует отметить, что умножение комплексного

ция времени, описывающая изменение тока в цепи во времени (мгно-

103

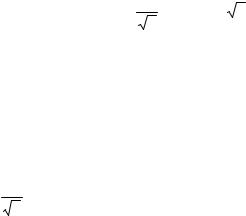
венное значение), есть мнимая часть комплексного значения тока: Im(Ime j (ω t +ψ i ) )= i(t) . Именно это соотношение позволяет утверждать,

что между мгновенным значением синусоидальной величины и ее символическим изображением существует однозначное соответствие.

При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения, сокращенно их называ-

ют комплексными значениями I , а соответствующие им векторы на комплексной плоскости – векторами комплексных значений. Связь между комплексной амплитудой и комплексным действующим значением устанавливается по формуле:

Пример символического представления функции времени тока

плекс тока.

Совокупность векторов, символически изображающих синусоидальные величины одной частоты, представленную на комплексной плоскости, называют векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов. Векторные диаграммы, как правило, используются для качественной оценки расчетов и обеспечения их наглядности. Они являются графическим отображением математических соотношений, описывающих электрическую цепь.

104

1. Об однозначном соответствии символического изображе-

сумме мгновенных значений соответствует векторная сумма символи-

105

ческих изображений (векторы складываются по правилам векторной алгебры).

ванию функции во временной области соответствует деление вектора

на jω в комплексной области или поворот вектора на угол − π . 2

Таким образом, символический метод позволяет свести дифференциальные уравнения, которыми описываются цепи переменного тока во временной области, к виду алгебраических уравнений в комплексной области. Полученное таким образом решение можно затем перевести во временную область.

3.3.2.Законы Ома и Кирхгофа

всимволической форме

По I закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле электрической цепи, равна нулю, т.е.

∑ik = 0 .

В соответствии с теоремой о сумме I закон Кирхгофа в символической или комплексной форме записывается в виде

106

По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е. или

Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:

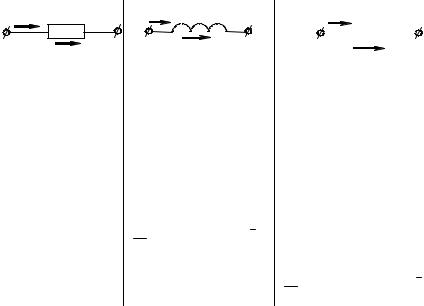
Рассмотрим закон Ома в символической форме записи для пассивных элементов цепи гармонического тока (рис. 3.15).

107

На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.

3.3.3.Последовательное соединение R, L, C

всимволической форме

По II закону Кирхгофа для схемы на рис. 3.17

На основании теоремы о сумме

Полное сопротивление равно модулю полного комплексного сопротивления Z = R2 + (X L − X C )2 , аргумент полного комплексного

108

где R – действительная часть комплексного сопротивления, назы-

вается активным сопротивлением, R = Z cos ϕ ; X – мнимая часть ком-

плексного сопротивления, называется реактивным сопротивлением,

X = Z sin ϕ = X L − X C .

Таким образом, закон Ома в символической форме общем виде

I = U , где Z может представлять, в частности, следующее: для со-

Z

π

противления Z = R , для индуктивности Z = jX L = X Le j 2 , для емкости

− j π

Z = − jX C = X C e 2 .

Введем понятие комплексной проводимости

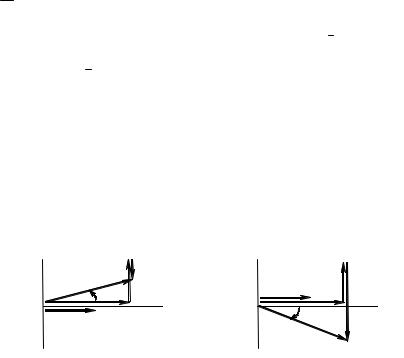
Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементов общим является ток, выберем вектор тока в качестве исходного вектора, направив его по действительной оси (рис. 3.18), и сориентируем по отношению к нему напряжения на R, L, C элементах.

Возможны три характера такой цепи:

109

Угол ϕ (разность начальных фаз напряжения и тока) определяется углом поворота вектора тока к вектору напряжения по кратчайшему пути: если поворот определяется против часовой стрелки, то ϕ > 0 (отстающий ток, индуктивный характер), иначе – ϕ <0 (опере-

жающий ток, емкостный характер). Как видно из приведенных выше формул, характер цепи определяет большее реактивное сопротивление.

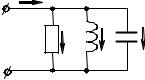
3.3.4.Параллельное соединение R, L, C

всимволической форме

ное значение тока

i(t) = iR (t) + iL (t) + iC (t) .

Согласно теореме о сумме

i(t) → I = I R + I L + IC .

Применим для каждой ветви закон Ома в комплексной форме:

110