книги / Механика сплошной среды. Законы сохранения

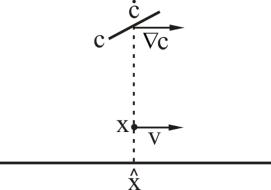
называемое конвективной производной, определяет скорость изменения за счет относительного движения совпадающих в данный момент материальной и пространственной точек. Формула (2.6) связывает скорость изменения величины c в материальной точке, находящейся в данный момент в фиксированной точке пространства, скорость изменения величины c в этой точке пространства и скорость переноса этой величины движущимся сквозь точку пространства континуумом. Приведем пример, когда пространство и континуум одномерны, а c — скалярное поле. На рис. 2.1 приведены материальная точка с именем x , ее текущее положение x в пространстве и

вектор скорости v , а также локальные наклон профиля c и вектор c .

Видно, что здесь v и c выбраны так, что v c 0. Скорость изменения c в точке x определяется разностью скорости изменения c материальной точки

x , т.е. c , и положительной величины v c . По смыслу в данной ситуации перенос материала сквозь точку x как раз должен уменьшать итоговое значение по сравнению с c .

Рис. 2.1. Материальная, пространственная и конвективная скорости

В частности, ускорение точки континуума выражается как

Пусть, например, нам требуется построить модель движения потока машин, свободно движущихся по дороге. Очевидно, ею будет уравнение

v vx v 0t

при начальном условии

v(x,0) v0 (x) .

Уравнение это означает, что скорость материальной частицы не зависит от времени, т.е. v( ,t) v0 ( ) . Это есть решение задачи с лагранжевой точки

32

зрения. Решение этой задачи с эйлеровой точки зрения столь простым не будет по следующей очевидной причине. Частицы-автомобили, имеющие постоянные, но неодинаковые скорости, вынуждены обгонять друг друга относительно дороги — пространственной оси, а это означает нарушение локальной топологии (близости), т.е. гипотезы континуума, и отсутствие непрерывности разыскиваемого решения v(x,t) по первому аргументу. С той же проблемой мы столкнемся и в рамках лагранжева описания, если

где x — радиус-вектор точки пространства. Правильнее этот радиус-вектор было бы поименовать y в соответствии с ранее принятым обозначением, однако не вызовет никакой путаницы употребление в аргументах полей обозначения x — по сути радиуса-вектора материальной точки, занимающей место y в пространстве. То есть движение считается известным, если в каждой точке области пространства, занимаемой континуумом, в каждый момент времени определена скорость движения континуума. Обычно эйлерово описание движения используется для сред, не обладающих памятью к предыстории движения, таких как многие газы и жидкости. Их состояние может быть полностью охарактеризовано значениями некоторых параметров в текущий момент времени, а информация об их значениях в прошлом является лишней. Очевидно, для таких сред эйлерово описание удобнее лагранжева. Для них функция справа (2.10) может даже не быть непрерывной по первому аргументу. Если же она непрерывна, то задача

— лагранжев закон движения, то есть данные два подхода являются теоретически эквивалентными, и от одного из них всегда можно перейти к другому. Гипотезой континуума при эйлеровом описании поэтому уместно считать требование непрерывности поля v( xˆ,t) по первому аргументу.

33

2.3. Скорость локального аффинного формоизменения

Материальным дифференцированием (1.7) с учетом (2.2) получаем

что материальная производная аффинора представляет собой линейный оператор, связывающий бесконечно малый материальный отрезок в отсчетной конфигурации и вектор относительной скорости его концов. Данный оператор таким образом описывает скорость локального аффинного формоизменения, но применим только в рамках лагранжева описания. Аналогичный оператор в рамках эйлерова описания должен связывать бесконечно малый материальный отрезок в текущей конфигурации и вектор относительной скорости его концов:

Он содержит в себе информацию о скорости локального аффинного формоизменения. Этот градиент скорости разлагается на симметричную и антисимметричную части, обозначаемые как

и называемые соответственно тензором деформации скорости и тензором вихря. Смысл первого названия проясняется из

и рассмотрим материальный отрезок dl , расположенный в текущий момент вдоль любого из главных направлений тензора деформации скорости. Тогда относительная скорость концов этого отрезка складывается из двух

34

составляющих — за счет локальной деформации материала D dl и его локального вращения W dl . Первая компонента есть скорость изменения длины этого отрезка, вторая — скорость его поворота. Материальные отрезки вдоль других направлений в дополнение ко всему испытывают поворот и за счет деформации локального объема.

Таким образом, в рамках эйлерова описания имеется лишь один тензор, отвечающий за локальную скорость деформации материала, — тензор деформации скорости D .

Получим скорости изменения векторов текущего локального базиса. Из

2.4. Спины эллипсоидов деформации

Меры деформаций вводились выше в терминах правого или левого трехгранников, поэтому и скорости таких мер уместно находить в этих терминах. Но для этого потребуется сначала найти скорости изменения трехгранников.

Меры деформации локального материального элемента принципиально определяются только в терминах лагранжева подхода. Следовательно, скорости их изменения находятся с использованием материального дифференцирования.

Непрерывность движения континуума ведет к тому, что при t t0 pi , pi pi , а этот предельный трехгранник является трехгранником главных осей тензора малых деформаций , а также трехгранником главных осей тензора деформации скорости при t t0 . Очевидно, pi 0. С использованием (1.38), (1.41), (1.42) введем антисимметричные тензоры спинов трехгранников:

35

Из (2.35) следует, что спин правого трехгранника определяется только тензором деформации скоростей, в отличие от спина левого трехгранника и спина , которые согласно (2.37), (2.38) определяются и тензором деформации скоростей, и тензором вихря. При t t0 имеем i , j 1, откуда

из (2.22) ij Wij , а спины , не определены.

2.5. Скорости мер деформаций правого семейства

Меры деформаций правого семейства определялись (1.52) как e ei pi pi , ei f ( i ) .

Выражение (2.39) показывает, что скорость изменения меры вызывается мгновенным изменением кратностей удлинений при фиксированном правом трехграннике и мгновенным поворотом этого трехгранника.

С учетом (2.34), (2.35) нормальные компоненты e в базисе правого трехгранника есть

(получается предельным переходом). В частных случаях семейства (1.45) скорости мер деформаций имеют компоненты:

базисе левого трехгранника. Компоненты скоростей мер деформации (2.42) и

37

(2.43) можно интерпретировать как ковариантные и контравариантные

деформации скорости D , совпадающему в этот момент с , причем быстрее всех это делает логарифмическая мера. С использованием (2.40), (2.41) и (1.44) может быть показано и что скорость любой меры деформаций вблизи отсчетной конфигурации сводится к D .

Полученные соотношения могут быть записаны в безындексном виде. Например, (2.42) принимает вид

2.6. Скорости мер деформаций левого семейства

Меры деформаций левого семейства вводились (1.53) как e ei pi pi .

Но нам сейчас понадобится связь мер левого и правого семейств (1.54) e RT e R ,

дифференцируя которую, получаем

правого трехгранника. Соотношение (2.48) взаимно-однозначно связывает скорости мер деформаций правого и левого семейств.

2.7. Другие меры скоростей деформаций

Определенные выше меры скорости деформации (за исключением D ) страдают туманностью геометрического смысла. Поэтому рассмотрим другие точки зрения на определение мер скоростей деформаций

Сначала найдем материальную производную меры e :

38

Выражение (2.51) показывает, что скорость изменения меры вызывается мгновенным изменением кратностей удлинений при фиксированном левом трехграннике и мгновенным поворотом этого трехгранника. В этом выражении, как и в аналогичном выражении для скоростей мер правого

описывающие мгновенные скорости деформирования эллипсоидов деформации (исключая их повороты). Связь таких мер очевидна:

Неудобство таких мер по сравнению с ранее введенными заключается в их неголономности, причина которой кроется в использовании неголономных реперов правого и левого трехгранников, однако законы состояния некоторых (пластических) сред сами по себе не могут быть голономными.

Все введенные выше меры, за исключением D , обладают абсолютной памятью об отсчетной конфигурации. С физической точки зрения такая память допустима лишь для упругих сред и сомнительна с точки зрения описания пластически деформируемых сред.

Но возможно развить идею определения скорости относительно

подвижной системы отсчета. При определении скоростей e,e ,e была молчаливо использована некая пространственная система отсчета, из которой мы следили за движением точек континуума, отмечая их текущие положения радиус-векторами. Пусть репер ai произвольно движется (вращается или даже деформируется) относительно данной системы отсчета. Скорость

где ai — взаимный к ai репер. Такие скорости тензоров деформаций при подборе конкретного репера отличает ясность смысла, что при построении уравнений состояния играет важную роль.

39

Если в качестве репера взят текущий основной базис ei , то получаем (с использованием (2.56) и (2.24))

— производную Коттера ‒ Ривлина. Эти две производные представляют собой примеры конвективных производных, потому что определены с точки зрения деформируемого репера. Можно показать, что

Если репер вращается как жесткое целое, то соответствующие производные называются коротационными. Примерами таких производных

называют производной Яуманна. Здесь читателю надлежит определить

Нетрудно выразить эту величину и через скорости мер деформаций. Например, через логарифмическую меру с использованием (2.46) получаем