книги / Механика сплошной среды. Законы сохранения

Исследователи по разным причинам не работают с какой-либо одной мерой деформации. От одной меры всегда можно перейти к другой, так что все меры одинаково ценны, и нет оснований какой-либо одной присваивать наименование «истинная». На рис. 1.4 для качественного сравнения приведены зависимости различных мер деформации от кратности при

одноосном удлинении среды: 1 — меры Грина 21 ( 2 1) , 2 — левой меры относительных удлинений 1, 3 — логарифмической меры ln , 4 — правой меры относительных удлинений 1 1 , 5 — меры Альманси 21 (1 12 ) .

Рис. 1.4. Зависимости мер деформаций от удлинения

Следует заметить, что все меры деформации неодинаково ведут себя при растяжении и сжатии. Например, при деформировании стержня со

растяжению, кривая 2 — сжатию).

21

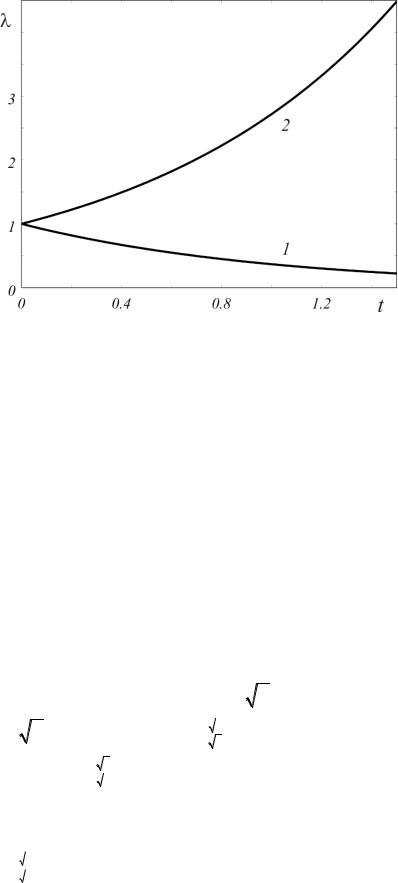
Рис. 1.5. Зависимость удлинения при растяжении и сжатии

1.7. Изменение материальной площадки и объема

Рассмотрим, как изменяется малая материальная площадка при ее аффинной деформации. Возьмем в K0 пару произвольных малых материальных отрезков, dx и dx , исходящих из некоторой материальной точки, и рассмотрим построенный на этих отрезках малый материальный

на локальных материальных базисах рассматриваемой материальной точки в

Перемножая любое из соотношений (1.55) скалярно само на себя и используя

(1.29), (1.30), получим

Наконец, следует установить связь локальных материальных объемов в K0 и Kt . Проще всего для этого рассмотреть малый материальный шар

Эта величина называется кратностью изменения объема. Из (1.58) и

определений (1.36), (1.37), (1.39) следует

Можно выразить данную величину и через меры деформаций (1.46), (1.47), (1.50), (1.51):

1.8. Перемещения и дисторсии. Малые деформации

Вектор перемещения точки тела из отсчетной конфигурации в

С помощью этого векторного поля на теле аффиноры могут быть записаны как

F x x u I u ,

(1.64)

F x x u I u ,

где диады u и u называют тензорами дисторсий. Эти тензоры несут в себе столько же информации, сколько и аффиноры, поэтому с их помощью можно записать все меры деформаций. Например, меры Грина и Альманси записываются как

23

Рассмотрим приближение малых деформаций, означающее, что конфигурации Kt и K0 деформированного тела мало различаются друг от друга, что подразумевает малость искажения материальной системы координат, искажения локального материального базиса и изменения материальной метрики. Это означает возможность работы в отсчетной пространственной системе координат с неизменными координатами i ,

координаты точки пространства, в которой первоначально находилась материальная точка с координатами i ) и набла-вектором e i i ei i ,

без привлечения текущей системы материальных координат. Аргументами всех определенных на континууме полей берут пространственные координаты i . Близость конфигураций подразумевает |u| 1 и, что более важно, |u | 1. Все меры деформации в этом случае до малых более высокого порядка по u сведутся к тензору

называемому тензором малых деформаций. Относительно тензоров Грина и Альманси в этом можно убедиться с помощью (1.65). Оператор

то есть смысл тензоров малых деформаций и поворотов как линейных операторов. Относительное перемещение du концов малого материального

(1.73)

выражается через

(1.74)

Очевидно, что главные оси тензора малых деформаций совпадают с предельными главными осями pi эллипсоидов деформации.

Малые упругие деформации без поворотов и перемещений испытывают, например, детали строительных конструкций. Главные относительные удлинения сводятся к i 1 i до малых второго порядка по

i . При этом все шкалы деформации f ( i ) с той же точностью стремятся к

i . Поскольку локальными поворотами можно пренебречь, меры

деформации сводятся к тензору малых деформаций.

Существуют среды, физически неспособные испытывать деформации ( i 0) , но при этом имеют конечные локальные перемещения и повороты. Таковы, например, нерастяжимые гибкие нити и ткани. Надуваемые резиновые сферические оболочки, напротив, обнаруживают большие деформации без поворотов. Другие же среды имеют сравнимые (малые или немалые) деформации и повороты. При необходимости можно построить локальные меры деформаций и ротаций, наиболее подходящие рассматриваемому процессу.

1.9. Условия совместности деформаций

Итак, все меры деформаций определяются полем перемещений точек материального континуума. Попробуем сейчас решить обратную задачу — по заданному полю меры деформации определить поле перемещений. Этот вопрос потребуется далее для постановки краевой задачи в напряжениях. Потребуем только непрерывности этого поля меры деформации вплоть до производных второго порядка, а в остальном будем считать его вполне произвольным. Сначала решим эту проблему для малых деформаций. Математически она эквивалентна интегрированию системы шести дифференциальных уравнений (1.66)

u u 2

с заданными правыми частями требуемой непрерывности. В ортобазисе ki декартовой пространственной системы координат эти уравнения запишутся в виде

25

достаточно гладких полей симметричного тензора на теле подпространство совместных деформаций. Уравнения (1.79) иногда записывают с использованием символического оператора несовместности

Ink :

Дадим геометрическую интерпретацию полученного условия. Сначала разделим еще недеформированную сплошную среду на бесконечно малые материальные кубики и разнесем их в пространстве, чтобы они не мешали друг другу. А затем сообщим каждому из них деформацию, соответствующую достаточно непрерывному, а в остальном произвольному полю деформаций, заданному на исходной конфигурации K0 материальной среды. Можно ли обратно склеить из деформированных параллелепипедов какое-либо непрерывное тело?

Чтобы ответить на этот вопрос, попробуем описать то, что мы сделали, в терминах дифгеометрии, при этом не ограничиваясь малыми деформациями. Пусть в K0 задана декартова система лагранжевых координат

и тензор Римана ‒ Кристоффеля (тензор кривизны пространства)

а это означает, что деформированный материальный континуум образует риманово пространство. Последнее сводится к аффинному пространству при условии

27

декартовых пространственных координатах. Условие (1.84) требует, чтобы конфигурация Kt принадлежала пространству без кривизны, то есть аффинному пространству. В общем же случае задаваемая произвольным полем деформации конфигурация Kt оказывается принадлежащей риманову пространству или, иначе говоря, не существует поля перемещений, переводящих K0 в Kt в аффинном пространстве.

Меру деформации aij в (1.85), конечно, можно выразить через любой

из тензоров конечных деформаций. Условие (1.85) или (1.86) содержит 6 независимых уравнений в трехмерном случае, одно в двумерном и ни одного в одномерном (столько независимых компонент у тензора Римана ‒ Кристоффеля).

1.10. Определение перемещений по совместным деформациям

Ограничимся малыми деформациями. Используя (1.69), (1.75), (1.78), получим

ab f (v)(b v)dv , получим

M

u u0 0 ( x x0 ) ( x x) ( ) dx (1.87)

M0

—формулу Чезаро. Очевидно, интеграл в (1.87) не зависит от пути. Перемещение, естественно, оказалось определенным с точностью до малого

28

перемещения среды как жесткого целого u0 0 (x x0 ), складывающегося

из трансляции точки M0 и поворота вокруг нее.

Формула Чезаро ввиду громоздкости подынтегральных выражений для вычисления перемещений не применяется, для чего имеется другой путь. Сначала находятся компоненты тензора дисторсии. Диагональные компоненты тензоров дисторсии и малых деформаций совпадают, а недиагональные находятся так. Из (1.66), (1.69), (1.70) в ортобазисе декартовой пространственной системы координат получаем

Интеграл в последнем выражении берется по ломаной со звеньями, параллельными осям координат (примем M0 (0,0,0) , M (x1, x2 , x3 ) ):

29

2.Кинематика сплошной среды

2.1.Материальная производная

На деформируемом материальном континууме бывают определены некоторые физические поля (например, перемещений или сил), изменяющиеся со временем. Для определения скорости изменения значений этих полей в фиксированных материальных точках используется

материальная производная:

При лагранжевом способе описания движения все поля рассматриваются как функции лагранжевых координат (не зависящих от времени) и времени, и потому для любого такого поля c( x,t ) правомерны записи (2.1)

в виде

2.2. Эйлеров способ описания движения

Эйлеров способ описания движения континуума заключается в рассмотрении всех заданных на нем полей как функций пространственных координат и времени. Чтобы перейти от лагранжева описания к эйлерову, нужно знать, какая именно материальная точка находится сейчас в данной точке пространства. Связь (1.2)

x x(xˆ,t)

как раз и содержит в себе такую информацию. Подставляя в c( x,t) эту связь, получим c c(x(xˆ,t),t) cˆ( xˆ,t) — эйлерово описание поля c . Ранее мы уже встречались с разновидностью эйлерова описания, когда рассматривали приближение малых деформаций.

Пусть требуется записать материальную производную поля c cˆ( xˆ,t) , т.е. заданного эйлеровым способом как функции пространственных координат и времени. В соответствии с (2.1) для этого необходимо взять производную c cˆ( xˆ,t) по t при фиксированном x . Очевидно фиксировать

30