
книги / Скреперы
..pdf
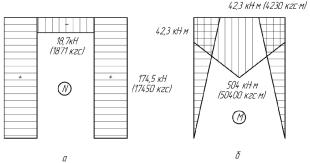
Эпюра изгибающих моментов от единичной силы, приложенной в т. D', показана на рис. 13, а. Эпюра изгибающих моментов от внеш-
них нагрузок дана на рис.13, б. Рц1 = 81027,7 Н·м, Рц2 = 190908,3 Н·м.
Рис. 13. Эпюры моментов
Определяем коэффициенты δ11 и ∆1p Для каждого участка берем площадь эпюры и умножаем на ординату этой же эпюры, проходящую через ее центр тяжести:
δ 11= l В l+ |
1 l l |
2 l 2 (м3 ), |
||||||||||
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
δ 11= 2,97 3,3 2,97+ |
1 2,97 |
2,97 |
2 |
2,97 |
2= 46,57 (м3 ). |
|||||||
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
Здесь множитель |
1 |
|
|
опущен. |
|
|
|
|||||
|
|
|
|
|
||||||||
E J |
|
|
|
|||||||||
Определим далее коэффициент ∆ 1 p : |
|
|
|
|||||||||
|
Р |
с |
Р |
+ Р |
|
|
|
|||||
∆ 1 p= 2 |
ц1 |
|
|
|
l+ |
|
ц1 |
|
ц2 |
c |
l ( |
Н м3 ). |
2 |
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
81027,7 |
0,853 |
81027,7 + 190908,3 |
|
∆ 1 p= |
2 |
2 |
2,97+ |
0,853 |
2,97 = |
|
|
|
2 |
|
= 871587 (H м3 ).
Множитель 1 опущен.
EJ
31
Находим Х1: |
|
|
|
|
|
|
|
|
|
X1 = |
−∆ 1 p |
. |
|
|
|
|
||||
|
|
|
|
|
δ 11 |
|
X1 = |
−∆ 1 p |
= |
871587 |
= 18715 (H) ≈ 1871,5 (кгс). |
||
δ 11 |
|
|||||
|
46,57 |
|
|
|
||
Усилие RDy |
равно Х1, тогда |
|
|
|||
|
|
RDy = 1871,5 кгс ≈ 18715 Н. |
||||
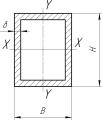
Эпюры продольных сил и изгибающих моментов показаны на рис. 14. Усилия расположены в плоскости рамы.
Для дальнейших расчетов необходимо вновь рассмотреть расчетную схему рис. 12, в которой теперь известны все опорные реакции. Рассматривая, как и раньше, только характерные точки 1, 2, 3, 4, 5 (см. рис.12, б), построим эпюру изгибающих моментов Мв в вертикальной плоскости.
Рис. 14. Эпюры продольных сил (а) и изгибающих моментов (б)
Как правило, опасными сечениями для продольных тяг рамы являются сечения в месте соединения их с поперечной балкой. Максимальные нормальные напряжения определяются по зависимости
σ = |
M Y |
± |
M |
в X |
± |
N |
(11) |
|
|
|
|
|
, |
||||
|
|
|
|
|||||
|
J x |
|
|
J y |
|
F |
|
|
32
где М, Мв — значения изгибающих моментов в боковой и в вертикальной плоскостях для рассматриваемого сечения тяг рамы;
Jx, Jy — моментыинерциисеченийотносительноосейХ—ХиY—Y; Х, Y — координаты рассматриваемой точки сечения тяг;
N — продольная сила;
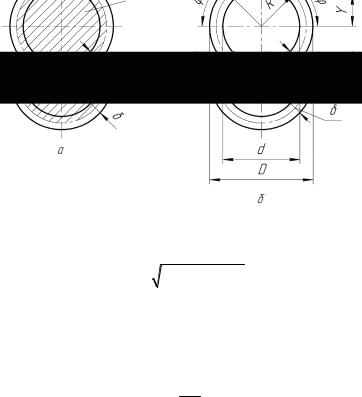
F — площадь поперечного сечения тяги рамы. Для полых балок прямоугольного сечения
(рис. 15) имеет место [11]:
|
|
δ H 3 |
|
|
|
B |
|
|||
J x |
= |
|
|
|
|
3 |
|
|
+1 ; |
|
6 |
|
H |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
δ B3 |
|
|
|
B |
|
||
J x |
= |
|
|
|
|
3 |
|
|
|
+1 ; |
6 |
|
H |
||||||||
|
|
|
|
|
|
|||||
F = 2δ (B+ H ). |
Рис. 15. Сечение |
На поперечную балку кроме изгибающих |
прямоугольной балки |
моментов и поперечных сил действует крутящий момент. В средней точке 3 (см. рис. 12, б) поперечной балки, кроме нормального напряжения необходимо найти касательные напряжения от крутящего момента и поперечной силы в элементах сечения балки. Касательные напряжения определяются по формулам:
для полок сечения
τ = |
Мкр |
+ |
Qx S y |
, |
(12) |
2F ′ δ п |
2J y δ п |
для стенок сечения
|
Мкр |
Qy Sx |
|
||
τ = |
|
+ |
|
, |
(13) |
2F ′ δ ст |
2J x δ ст |
||||
где F ′— площадь, охватываемая средней линией замкнутого про- |
|||||
филя сечения балки (рис.16, а); |
|
|
|
||
δ ст , δ п — толщинастенкииполкиврассматриваемойточкесечения; |
|||||
Qx , Qy — поперечные силы в сечении; |
|
||||
Sx , Sy — статические моменты |
сопротивления |
относительно |
|||
осей X—X и Y—Y для отсеченной части сечения.
33
Для поперечной полой балки круглого сечения (рис.16, б) имеет место:
|
|
|
π (D4− d 4 ) π D4 |
|
4 |
|
|
|
d |
|||
J x |
= J y |
= |
|
|
= |
|
(1 − α |
|
),α = |
|
||
64 |
|
|
|
D, |
||||||||
|
|
|
64 |
|
|
|
|
|
||||
|
Sx = S y = 2δ |
R2 cos ϕ , ϕ = arcsin |
Y |
, |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
где Y — координата рассматриваемой точки сечения;
δ = δ п= δ ст.
Рис. 16. Сечение балки цилиндрической формы
Приведенное напряжение в опасной точке сечения
σ = |
σ + σ |
+ τ 4 |
2 |
, |
|
2 |
2 |
|
|
пр |
x |
y |
|
|
где σ x σ, y вычислены по формуле (11), a τ |
|
взято наибольшее из по- |
||
лученных по формулам (12) и (13).
Коэффициент запаса прочности балки без учета концентрации напряжений
n = [σ ] ,
σ пр
где [σ ] — допускаемое напряжение.
34
6.2.Расчет на прочность упряжных тяг
Вкачестве примера рассмотрим порядок расчета на прочность упряжной тяги 4 в сечении VII—VII (см. рис.10).
При расчете предполагаем, что опоры D и D' представляют собой подвижные шарниры и искривление нейтральной оси тяги не учитывается.
Сечение VII—VII находится от оси упряжного шарнира на расстоянии l = 300 мм.
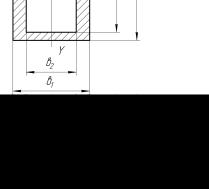
Рис. 17. Геометрические характеристики сечения
1. Площадь сечения
F = F1 − F2 , F1 = h1 b1 , F2 = h2 b2 ,
где F1, F2 — площадь, ограниченная наружным и внутренним контуром сечения.
В нашем случае (рис. 17)
F= 25 10 − 22, 2 7, 2 = 90,16 (см2 ).
2.Момент сопротивления сечения относительно оси Z—Z:
W |
= |
b1 h13 − b2 h23 |
, |
|
|||
z −z |
|
6h1 |
|
|
|
||
где b1 , b2 — ширина сечения по наружному и внутреннему контуру; h1 , h2 — высота сечения по наружному и внутреннему контуру.
35
Таким образом,
W |
= |
10 253 − 7, 2 22, 23 |
|
= 516,5 (см3 ). |
|
|
|||
|
|
|
|||||||
z −z |
6 |
25 |
|
|
|
|
|
||
|
|
|
|
|
|
||||
3. Определение напряжений в сечении осуществляется по |
|||||||||
формулам: |
|
|
|
|
|
|
|
|
|
для нормальных напряжений изгиба σ z= |
M z |
; |
|
|
|||||
|
|
|
|||||||
|
|
|
|
|
|
Wz |
|
|
|
для нормальных напряжений растяжения-сжатия σ N = |
N |
. |
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
F |
|
Полное напряжение в сечении |
|
|
|
|
|
||||
|
|
σ = σ +z σ N . |
|
|
|
|
|
||
Изгибающий момент в сечении определяется по формуле |
|||||||||
|
|
M z = RDz l. |
|
|
|
|
|
||
Нормальная |
сила в |
сечении |
N = RDx . Тогда |
|
имеем: |
||||
σ z= − 377 кгс/см2 |
и σ N = − 102 кгс/см2. |
Полное напряжение равно |
|||||||
479кгс/см2.
При значении предела текучести для материала упряжных тяг
сталь 15ХСНД σ т= 3500 кгс/см2 имеем запас прочности.
Аналогично рассчитываются и другие сечения упряжных тяг. Результаты расчетов сводятся в таблицу.
6.3. Расчет на прочность поперечной балки тяговой рамы
Поперечная балка тяговой рамы скрепера представляет собой трубчатую конструкцию. Рассмотрим сечение III—III (см. рис.10)
иопределим действующие напряжения.
1.Момент сопротивления сечения изгибу:
Wx = Wz |
= |
π |
(D4 − d 4 ), |
|
|||
|
|
32D |
|
где D и d — наружный и внутренний диаметры трубы. Таким образом, момент сопротивления изгибу (рис.18)
Wx = Wz |
= |
3,14 |
(35,14 − 32,74 ) = 1046,855 (см3 ). |
|
|||
|
|
32 35,1 |
|
36
2. Момент сопротивления сечения кручению [9]:
Wкр = π D3 (1 − α 4 ), 16
где α = d / D.
Тогда Wкр = 2Wx = 2 1046,855 = 2093, 73 (см3 ).
3. В рассматриваемом сечении трубы (см. рис. 18) действуют изгибающие моменты [17]:
M x |
= RDz |
|
|
l |
|
− Pц cos γ |
l |
− lц |
, |
||
|
|
|
|
||||||||
|
|
2 |
|
2 |
|
|
|||||
M z |
= RDx |
|
l |
− Pц sin γ |
l |
− lц |
, |
||||
|
|
||||||||||
|
|
2 |
|
2 |
|
|
|||||
где l — длина поперечной балки;
lц — расстояние от торца поперечной балкидосеченияустановкигидроцилиндров.
Крутящий момент
M кр = RD lт,
где lт — длина упряжной тяги.
4. Нормальные напряжения изгиба
Рис. 18. Геометрические характеристики сечения трубы
σ x= |
M x |
,σ =y |
M z |
. |
|
|
|||
|
Wx |
Wz |
||
5.Касательные напряжения кручения
τ= M кр . Wкр
6.Приведенные напряжения в сечении III—III по теории Мора
σ = |
σ + σ |
+ |
τ 4 |
2 |
. |
|
2 |
2 |
|
|
|
пр |
x |
y |
|
|
|
Аналогично определяются напряжения и в других сечениях поперечной балки. Результаты расчета удобно свести в итоговую таблицу.
Запас прочности определяется по формуле
n = |
σ т |
≥ 1. |
|
||
|
σ пр |
|
37
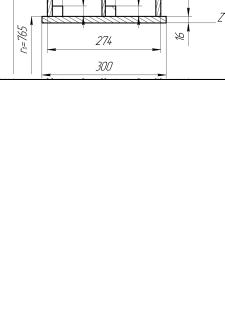
6.4. Расчет хобота
Рассмотрим сечение VI—VI хобота (см. рис. 10). На рис. 19 показаны размеры поперечного сечения хобота для варианта конструкции скрепера (пример).
1. Площадь сечения определяется по правилу расче-
|
|
|
та площадей: |
||||||
|
|
|
|
|
|
F = a b, |
|||
|
|
|
где a — длина, мм; |
||||||
|
|
|
|||||||
|
|
|
|
b — ширина, мм. |
|||||
|
|
|
F = 2 47,5 1, 2 + 47,5 0,8 + |
||||||
|
|
|
+30 1,6 + 30 1, 2 + 2 2,5 2,5 = |
||||||
|
|
|
|
|
|
= 248,5 (см2 ). |
|||
|
|
|
|
|
|
||||
|
|
|
|
2. Координаты центра тя- |
|||||
|
|
|
жести: |
||||||
|
|
|
Yo |
= |
2F1 Y1 + F2 Y2 + F3 Y3 |
+ |
|||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F |
|||
|
|
|
|
|
+ |
F4 Y4 + 2F5 Y5 |
, |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F |
|||
|
|
|
где |
F1—F5 — площадь со- |
|||||
|
Рис. 19. Поперечное сечение хобота |
ставляющих сечения (стенки, |
|||||||
|
|
|
перемычки, нижней полки, |
||||||
верхней полки, технологических элементов); |
|||||||||
|
Y1—Y5 — соответствующие координаты центров тяжести со- |
||||||||
ставляющих площадей. |
|
|
|
|
|
|
|
||
Yo |
= |
114 25,35 + 38 25, 25 + 48 0,8 + 36 49,7 +12,5 2,85 |
= 23 (см). |
||||||
|
|||||||||
|
2478,5 |
|
|
|
|
|
|
|
|
Аналогично
Zo = −6, 25 11, 25 + 6, 25 1,55 − 38 0,1 = −0, 26 (см). 248,5
38
3. Момент инерции сечения относительно оси Zo:
|
|
|
b h3 |
|
|
|
b |
h3 |
|
|
|
|
|
b |
h3 |
||||
J |
Zo |
= 2 |
|
1 |
1 |
+ F a2 |
+ |
2 |
2 |
|
+ F a2 |
+ |
|
3 |
|
3 |
+ |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
12 |
1 1 |
|
12 |
2 2 |
|
12 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
b h3 |
|
|
|
b h3 |
|
|
|
|
|
|
||||
|
+F a2 |
+ |
4 |
4 |
+ F a2 |
+ 2 |
|
5 5 |
+ F a2 |
, |
|
||||||||
|
|
|
|
|
|
||||||||||||||
|
|
3 |
3 |
|
12 |
|
4 |
4 |
|
12 |
|
|
5 |
5 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где bi и hi — соответственно ширина и высота составляющих се-
чения;
ai — расстояние от собственного центра тяжести составляющего сечения хобота до оси.
Тогда
JZo |
= 2 |
1, 2 47,53 |
+ 114 2,352 + |
0,8 47,53 |
+ 38 2,352 + |
30 1, 63 |
+ 48 22, 22 + |
||||
|
|
|
|
||||||||
|
12 |
|
12 |
|
12 |
|
|||||
|
+ |
30 1, 23 |
+ 36 26, 72 + 2 |
2,5 2,53 |
+ 12,5 20,152 = 838353 (см4 ). |
||||||
|
|
|
|||||||||
|
12 |
|
12 |
|
|
|
|
||||
4. Радиус кривизны оси бруса
ρ = rв + yo ,
где rв — внутренний радиус кривизны сечения; yo — ордината центра тяжести сечения.
ρ= 749 + 230 = 979 (мм).
5.Радиус кривизны нейтрального слоя:
r = |
∑bi |
hi |
, |
||
∑bi ln |
rн |
||||
|
|
||||
|
rв |
|
|||
|
|
|
|
||
где bi , hi — ширина и высота элемента сечения;
rн, rв — наружный и внутренний радиусы кривизны элемента сечения.
В нашем случае
r = |
30 1,6 + 2 2,5 2,5 + 2 1, 2 47,5 + 0,8 47,5 + 30 1, 2 |
= 96,1 (см), |
||||||||||
30ln |
76, |
5 |
+ 2,5ln |
79 |
+ 1, 2 ln |
124 |
+ 0,8ln |
124 |
+ 30ln |
125, 2 |
||
|
|
9 |
76,5 |
|
|
|
|
|||||
|
74, |
|
76,5 |
76,5 |
124 |
|
||||||
где ln — натуральный логарифм отношения.
39

6. Момент сопротивления кручению
Wкр = 2 F δ ,
где F и δ — площадь, охватываемая средней линией контура, и толщина стенки хобота.
Wкр = 2 48,9 26, 2 1, 2 = 3074,8 (см3 ).
7. Определение напряжений в сечении хобота. Силы RЕ, RK и FK, приложенные к поворотно-сцепному устройству, относительно рассматриваемого сечения раскладываются по двум направлениям: N — нормально к сечению и Q — в плоскости сечения. При перенесении сил в центр тяжести сечения в последнем возникает изгибающий
момент My.
Нормальное усилие в сечении VI—VI:
N = RE cos γ + RK cos γ + FK sin γ .
Поперечная сила в сечении VI—VI:
Q = RE sin γ + RK sin γ + FK cos γ .
Изгибающий момент в сечении VI — VI:
M = ((R + R )cos γ + F sinγ )l + ((R + R )sinγ + F cosγ )l ,
z E K K 1 E K K 2
где l1 и l2 — расстояние от центра тяжести сечения VI—VI хобота до точки приведения усилий к поперечной балке тяговой рамы.
Для примера принимаем, что l1 = 785 мм и l2 = 700 мм. При N = = –18127 кгс, Q= 14683 кгс и Mz = 391129 кгc·м получим:
а) напряжения от изгиба в крайних точках сечения
σ сж= −M z (rн − rв ) ,
F (ρ − r)rн
где rн — наружный радиус кривизны (в нашем случае rн = 1252 см); r — радиус кривизны нейтрального слоя ( r = 961 см);
ρ — радиус кривизны бруса ( ρ |
= 979 см). |
||||
σ p= |
M |
|
|
(r − rв ) |
, |
F |
|
(ρ − r )r |
|||
|
|
|
|
в |
|
где rв — внутренний радиус кривизны ( rв = 749 см);
40
