
книги / Общая физика. Гидродинамика и теплообмен
.pdfdA = − σ dS . |
(2.12) |
Знак минус указывает на то, что увеличение поверхности dS > 0 сопровождается отрицательной работой dA < 0, а уменьшение поверхности dS < 0 − положительной dA > 0.
Коэффициент σ > 0 является основной величиной, характеризующей свойства поверхности жидкости. Он называется коэффициентом поверхностного натяжения. Коэффициент поверхностного натяжения измеряется работой, необходимой для изменения на единицу площади поверхности жидкости при постоянной температуре. В СИ σ имеет размерность Дж/м2.
Из курса общей физики известно, что работа равна со знаком
минус изменению потенциальной энергии dA = −dU , поэтому |
|
dU = σ dS , U = σS . |
(2.13) |
Поскольку энергия U обязана своим происхождением наличию поверхности жидкости, то она пропорциональна площади S этой поверхности. Теперь ясно, что указанные выше особые условия, в которых находится поверхность жидкости, заключаются в том, что поверхность жидкости обладает избыточной по сравнению с остальной массой жидкости потенциальной энергией.
Всякая система при равновесии находится в том из возможных для нее состояний, при котором ее энергия имеет минимальное значение. В нашем случае это означает, что жидкость, находящаяся в равновесии, должна иметь минимально возможную поверхность, следовательно, должны существовать силы, стремящиеся сократить эту поверхность.
Очевидно, что эти силы должны быть направлены вдоль самой поверхности по касательной к ней. Эти силы называются силами поверхностного натяжения. Нужно, однако, помнить, что первопричиной возникновения сил поверхностного натяжения являются межмолекулярные силы, испытываемые молекулами поверхностного слоя, направленные перпендикулярно к поверхности (см. рис. 2.3).
Для разрыва или, как говорят, для раздела поверхности необходимо приложить внешние силы, параллельные поверхности и пер-
31

пендикулярные той линии, вдоль которой предполагается разрыв. Это особенно ясно видно из опытов с тонкими пленками жидкости.
Некоторые жидкости (например, мыльная вода) обладают свойством образовывать тонкие пленки. Если опустить проволочную рамку, одна из сторон которой подвижна (рис. 2.4), в мыльный раствор, то вся она затянется пленкой жидкости. Силы поверхностного натяжения принуждают пленку сокращаться, и подвижная перекладина АВ вслед за пленкой перемещается вверх.
Чтобы сохранить ее в равновесии, к перекладине нужно приложить силу Р
ввиде груза (сюда входит и вес самой перекладины). Таким образом, сила поверхностного натяжения f, действующая
впленке, перпендикулярна к линии АВ,
которая в данном случае и является одной из линий раздела.
Описанный опыт может быть использован для определения численного значения коэффициента поверхностного натяжения жидкости, образующей пленку. Действительно, поверхностная сила f, с учетом того, что пленка имеет две поверхности (пленка на самом деле представляет собой тонкий слой жидкости), равна при равновесии весу груза Р:
2 f = P; |
f = |
P |
. |
|
|||
|
2 |
|
|
Если под действием силы f перекладина переместилась на расстояние dh из положения АВ, то работа силы
dA = f dh = P dh = σl dh , 2
где l − длина рамки. Отсюда следует, что
σ = |
P |
. |
(2.14) |
|
|||
|
2l |
|
|
32
Коэффициент поверхностного натяжения (2.14) можно еще определить как величину, равную силе, действующей по касательной к поверхности жидкости, приходящейся на единицу длины линии раздела. Размерность σ в этом случае равна Н/м.
2.4.2. Граница жидкости и твердого тела
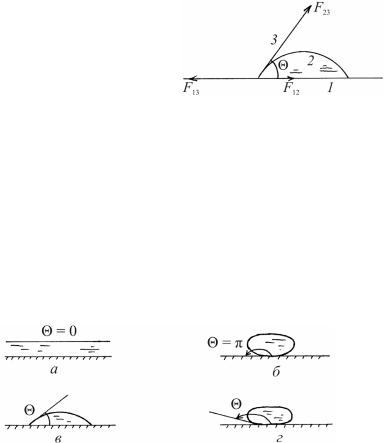
Пусть капля жидкости 2 (рис. 2.5) граничит с собственным паром 3 и с плоской поверхностью твердого тела 1. Форма поверхности жидкости зависит от соотношения сил взаимодействия молекул жидкости между собой Fж−ж и с моле-
кулами твердого тела Fж− тв . Введем краевой угол Θ – угол, образованный касательной к поверхности
жидкости (у ее границы с твердым |
|
|
телом) и поверхностью твердого |
Рис. 2.5 |
|
тела. Рассмотрим частные случаи. |
||
|
||
Если Fж−ж << Fж− тв и Θ = 0, то жидкость растекается тонким |
||
слоем по поверхности твердого тела. Это явление полного смачивания (рис. 2.6, а) характерно, например, для воды на чистом стекле.
Случай Fж−ж >> Fж− тв и Θ = π соответствует полному несмачива-
нию твердого тела жидкостью (рис. 2.6, б). Оно характерно для воды на парафине.
Большей же частью наблюдаются промежуточные случаи: частичного смачивания ( Θ < π/2), как это показано на рис. 2.6, в, или частичного несмачивания ( Θ > π/2) твердой поверхности (рис. 2.6, г).
Рис. 2.6
33
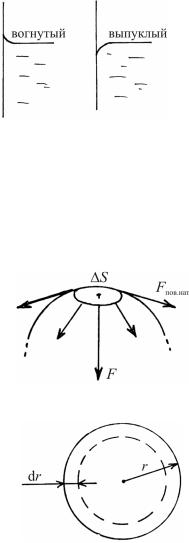
Взаимодействие частиц жидкости с частицами твердого тела влияет на форму поверхности жидкости, налитой в сосуд (рис. 2.7). Если большое количество жидкости налито в широкий сосуд, то форма ее поверхности определяется силой тяжести, которая обеспечивает плоскую и горизонтальную поверхность – зеркало. Однако
|
у самых стенок сосуда поверх- |
|
|
ность жидкости искривлена так, |
|
|
что образуется мениск, вогнутый у |
|
Рис. 2.7 |
смачивающих жидкостей и вы- |
|
пуклый у несмачивающих. |
||
|
2.4.3.Силы, возникающие на кривой поверхности жидкости
Вслучаях, когда поверхность жидкости оказывается искривленной, кривизна поверхности жидкости приводит к появлению дополнительных сил, действующих на жидкость под этой поверхностью
Рис. 2.8
Рис. 2.9
(рис. 2.8). Отсюда следует, что объем жидкости под сферической поверхностью несколько сжат, так как испытывает дополнительное давление p = F ∆S , направ-
∆S , направ-
ленное радиально, перпендикулярно к поверхности.
Данные соображения позволяют вычислить величину этого дополнительного давления р, связанного с кривизной поверхности. Пусть под действием этого давления жидкий шар (капля) уменьшит свой объем на dV, как это показано нарис. 2.9.
34
В этом случае работа сжатия жидкости dA = p dV . Она произ-
ведена за счет уменьшения поверхностной потенциальной энергии dU = σ dS , где dS – уменьшение поверхности шара, соответствующее уменьшению его радиуса на dr.
Из известных формул для поверхности и объема шара
S = 4πr2 ; |
V = |
4 |
πr3 |
|
|||
|
3 |
|
|
получаем очевидные выражения: |
|
|
|
dS = 8πr dr; |
dV = 4πr2dr . |
||
Подставляя эти значения для dS и dV в уравнения и принимая во внимание, что |dA| = |dU|, получаем формулу для давления, оказываемого на жидкость ее кривой поверхностью:
p = |
2σ |
. |
(2.15) |
|
|||
|
r |
|
|
Для поверхности произвольной (не сферической) формы давление, обусловленное кривизной поверхности, выражается уравнением Лапласа:
|
1 |
|
1 |
|
|
p = σ |
|
+ |
|
, |
(2.16) |
|
|
||||
r1 |
|
r2 |
|
||
где r1 и r2 – главные радиусы кривизны в данной точке поверхности в двух взаимно перпендикулярных сечениях.
Легко заметить, что формула для сферы (2.15) является частным случаем уравнения Лапласа (2.16), так как для сферы оба главных радиуса кривизны совпадают и равны радиусу сферы: r1 = r2 = r.
Дополнительное давление, определяемое формулой Лапласа (2.15), направлено к центру кривизны поверхности и перпендикулярно этой поверхности. Поэтому в случае выпуклой поверхности ( r > 0 ) оно направлено внутрь жидкости и добавляется к давлению жидкости. В случае же вогнутой поверхности (когда центр кривизны находится вне жидкости и r < 0 ) жидкость будет находиться под меньшим давлением, чем та же жидкость под плоской поверхностью.
35

2.4.4. Капиллярные явления
Поверхность жидкости имеет некоторую кривизну вблизи границы между жидкостью и твердой стенкой сосуда. В остальной своей части поверхность плоская. Однако, если общая величина поверхности невелика (например, жидкость находится в узком сосуде), влияние стенок простирается на всю поверхность жидкости и она оказывается искривленной на всем своем протяжении.
Если размеры сосуда r, в котором находится жидкость, или расстояние между поверхностями, ограничивающими жидкость, сравнимы с радиусом кривизны поверхности жидкости r0, то такой сосуд называется капиллярным (волосным). Явления, происходящие в таком сосуде, называются капиллярными.
Рассмотрим некоторые явления, связанные с капиллярностью. Так как для капиллярных сосудов характерна, прежде всего, кривизна поверхности жидкости, то здесь больше всего сказывается влияние дополнительного давления Лапласа. Непосредственным следствием этого является так называемый капиллярный подъем.
На рис. 2.10 изображена узкая трубка, опущенная в широкий сосуд с жидкостью, смачивающей стенки трубки. Тогда жидкость, проникшая в трубку, образует вогнутый мениск. Считаем, что трубка настолько узка, что ее радиус r сравним с радиусом r0 мениска. Вследствие давления, вызванного кривизной поверхности, жидкость, запол-
няющая трубку, испытывает давление p = 2σ , которое направлено r0
к центру кривизны мениска, т.е. вверх. Под действием этого давления жидкость поднимается по трубке до уровня h, при котором гидростатическое давление ρgh жидкости высотой h уравновешивает давление р. Условием равновесия будет, следовательно, равенство
36

2σ = ρgh , r0
где ρ – плотность жидкости; g – ускорение свободного падения.
Это равенство определяет высоту подъема жидкости h в капилляре следующим образом:
h = 2σ .
ρgr0
Однако удобнее в практических расчетах пользоваться связью между высотой подъема h и радиусом трубки r. Обратимся для этого к рис. 2.11, на котором мениск и капилляр изображены крупнее. Центр сферы, частью которой является мениск, находится в точке 0. Краевой угол жидкости, соприкасающейся со стенками капилляра, равен Θ . Из чертежа непосредственно следует, что r0 = r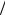 cosΘ .
cosΘ .
Поэтому
h = 2σ cosΘ .
ρgr
(2.17)
Рис. 2.11
(2.18)
В частности, для жидкости, которая полностью смачивает стенки капилляра и для которой, следовательно, Θ = 0 и cos Θ = 1, имеем
h = |
2σ |
. |
(2.19) |
|
|||
|
ρgr |
|
|
Как и следовало ожидать, высота подъема жидкости в капилляре (капиллярный подъем) растет с уменьшением радиуса капилляра и с
увеличением коэффициента поверхностного натяжения жидкости. |
|
Рассмотрим пример. Пусть диаметр капилляра d = 1 мкм |
= |
= 10−6 м, коэффициент поверхностного натяжения воды при 20 |
ºС |
σ = 72,5 10−3 Н/м, плотность ρ = 103 кг/м3, g = 9,8 м/с2, Θ = 0, тогда
по формуле (2.19) получаем для максимальной высоты капиллярного подъема воды h = 29,6 м.
37
Если жидкость не смачивает стенки капилляра, картина будет обратной, так как мениск теперь выпуклый, центр кривизны находится внутри жидкости, давление Лапласа направлено вниз. Уровень жидкости в капилляре будет теперь ниже уровня в сосуде, в который опущен капилляр (отрицательный капиллярный подъем).
Капиллярным подъемом объясняется ряд широко известных явлений: впитывание жидкости фильтровальной бумагой, изготовляемой так, чтобы в ней были узкие извилистые поры; подъем воды из почвы по стволам деревьев, в которых волокна древесины играют роль очень тонких капилляров, и другие явления.
2.4.5. Зависимость коэффициента поверхностного натяжения от температуры
Теоретически эта зависимость не может быть установлена, хотя качественно очевидно, что с повышением температуры t, ºС, значение коэффициента поверхностного натяжения должно уменьшаться. Приближенно температурная зависимость σ от t выражается линейным уравнением
σ = σ0 (1− k t ). |
(2.20) |
При критической температуре t = tкр исчезают различия между
жидкостью и паром, при этом коэффициент поверхностного натяжения σ становится равным нулю. Учитывая это обстоятельство, получаем k = 1/ tкр , тогда
|
|
|
t |
|
|
σ = σ0 |
1 |
− |
|
, |
(2.21) |
|
|||||
|
|
|
|
|
|
|
|
|
tкр |
|
|
где σ0 = 75,5 10−3 Н/м при t = 0 ºС для воды.
В заключение приведем значения σ для воды при некоторых температурах:
t, ºС |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
σ, 10–3 Н/м |
75,5 |
74,0 |
72,5 |
71,0 |
69,5 |
67,8 |
66,0 |
64,2 |
62,3 |
38 |
|
|
|
|
|
|
|
|
|
2.4.6. Капиллярное движение
Если поверхностное натяжение жидкости изменяется от точки к точке, то наряду с нормальным давлением на поверхности появляется дополнительная сила, направленная тангенциально к поверхности. Эта сила определяется градиентом поверхностного натяжения.
Тангенциальная сила, отнесенная к единице поверхности, имеет
вид
pτ = grad σ . |
(2.22) |
Положительный знак перед градиентом означает, что pτ стре-
мится привести в движение поверхность жидкости в направлении от мест с меньшим к местам с большим поверхностным натяжением.
Причиной, вызывающей изменение σ на поверхности жидкости, может служить изменение температуры этой поверхности. В этом случае возникает так называемая капиллярная конвекция.
Следует отметить, что влияние поверхности жидкости не может сказываться на движении крупного масштаба. Капиллярное движение становится заметным, если поверхность жидкости достаточно велика по сравнению с ее объемом (например, жидкость налита в мелкую широкую емкость).
Контрольные вопросы
1.Описать характер движения молекул жидкости.
2.В чем суть приближения сплошной среды?
3.Какие жидкости называются неньютоновскими?
4.Перечислитьпричины появления сил поверхностного натяжения.
5.Объяснить поведение жидкости на твердой поверхности.
6.Сформулировать физические причины дополнительного давления и привести формулу Лапласа.
7.Какие явления относятся к капиллярным?
8.Какова зависимость коэффициента поверхностного натяжения от температуры?
39
3.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КОНВЕКТИВНОГО ТЕПЛООБМЕНА
Под конвекцией теплоты понимают ее перенос движением текучей среды из области с одной температурой в область с другой. При этом перенос теплоты неразрывно связан с переносом вещества. Кроме конвективного теплопереноса необходимо учитывать теплопроводность жидкости.
3.1. Субстанциональная производная
Выберем какую-либо жидкую частицу движущейся среды. Полное изменение любой физической величины ϕ (скорости, плотности, температуры) элемента движущейся среды происходит по двум причинам: изменение во времени и изменение из-за движения этого элемента из одной точки пространства в другую. Так как ϕ = ϕ(x, y, z,t) ,
то полная производная по времени t будет иметь вид
|
dϕ |
= |
∂ϕ + |
∂ϕ |
dx |
+ |
∂ϕ |
dy |
+ ∂ϕ |
dz |
. |
(3.1) |
||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
dt |
∂t |
∂x dt |
∂y dt |
∂z dt |
|
||||||||||||||||
Введем составляющие скорости движения жидкой частицы |
|
|||||||||||||||||||||
|
|
vx |
= |
dx |
; |
vy = |
dy |
; |
|
vz |
= |
dz |
, |
(3.2) |
||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
dt |
|
|
|
dt |
|
|
|
|
dt |
|
||||||
тогда выражение (3.1) примет следующий вид: |
|
|||||||||||||||||||||
|
|
dϕ |
= ∂ϕ + vx ∂ϕ + vy |
∂ϕ + vz ∂ϕ . |
(3.3) |
|||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
dt |
∂t |
|
∂x |
|
|
∂y |
|
∂z |
|
|||||||||||
Последнее соотношение (3.3) |
называется субстанциональной |
|||||||||||||||||||||
производной, так как она связана с движущейся средой. В (3.3) |
∂ϕ |
|||
|
|
|
|
∂t |
представляет собой локальное, а vx |
∂ϕ + vy |
∂ϕ + vz |
∂ϕ – конвективное |
|
|
∂x |
∂y |
∂z |
|
изменение величины ϕ.
40
