книги / Порошковое материаловедение. Основы теоретического материаловедения

Рассмотрим случаи высоких и низких температур, где интересующая нас зависимость может быть получена наиболее просто. Затем, интерполируя полученные результаты, получим полный вид искомой зависимости. Однако, прежде чем приступить к решению этой задачи, уточним, что мы будем называть высокими и низкими температурами. Ясно, что определить их можно, лишь сопоставляя с некоторой характерной для данного материала температурой Т*. Выбор ее неоднозначен,

но обычно в качестве Т* берут температуру Дебая Θ. Она вхо-

дит как параметр в интерполяционную формулу Дебая для теплоемкости и интегрально характеризует строение вещества и взаимодействие его атомов. Температура Дебая Θ табулирована в справочниках как физический параметр вещества и для металлов обычно порядка нескольких сотен градусов.

При Т « Θ скорость электронов не зависит от температуры, поскольку электроны подчинены статистике Ферми–Дира- ка; с ~ Т согласно (83); l и становятся как угодно большими

и могут быть ограничены только дефектами решетки, т.е. от Т не зависят, поэтому из (81)–(82) следует

При Т » Θ скорость электронов = const (Т), так как при любых температурах в твердой фазе испытывают возбуждение лишь электроны вблизи поверхности Ферми; с = const (Т) –

закон Дюлонга и Пти; l и ограничены тепловыми колебаниями решетки и в первом приближении ( , l) ~ Т 1, поэтому из

(81)–(82) следует

Поскольку e (Т » Θ) < e (Т « Θ), то из (85)–(86) следует, что в промежуточной области температур e имеет локальный

111

максимум. Аналогично получаем, что (Т) – монотонная, невозрастающая функция.

В случае чисто фононной теплопроводности выражение для q совпадает по форме с (82), поскольку (82) верно для

любой газовой модели, только теперь с – решеточная тепло-

емкость, а – скорость фононов, которая определяется упругими свойствами кристаллов, а потому практически не зависит от температуры. Поэтому имеют место следующие соотношения:

сильнее уменьшается при удалении от максимума, пропорционально T 3 при Т < T * и ~ T 3 exp (Θ/Т) при Т > T *, тогда как

e ~ Т при Т < T * и ~ T 3 при Т > T *. Поэтому при произвольной температуре чаще всего теплопроводность диэлектриков много меньше теплопроводности металлов: λp < e.

Максимальная длина свободного пробега фононов при низких Т ограничена только размерами образца (так как длина волны фонона ~100 межатомных расстояний), поэтому при низких температурах λp зависит от размеров и формы образ-

цов. У электронов l ~ 1Ǻ и практически не зависит от Т, поэтому подобной зависимости σ и λe не наблюдается.

112

В табл. 4 приведены характерные значения параметров тепло- и электропроводностей чистых элементов. Откуда, в частности, видно, что температурная зависимость теплопроводности для всех элементов, кроме Si и Fe, в интервале 300– 1300 К не превышает ~ 30 %, а значит, в технических приложениях, как правило, не существенна.

113

Окончание табл. 4

*В скобках указана температура.

5.2.Влияние вакансий, примесей, дислокаций

имежзеренных границ на тепло- и электропроводность

Дефекты уменьшают длину свободного пробега электронов и фононов, а потому согласно (82)–(83) уменьшают тепло- и электропроводность материалов. Экспериментальные данные, как правило, указывают на ослабление влияния дефектов кристаллических решеток на теплопроводность материалов при увеличении температуры (табл. 5), поскольку растет концентрация фононов и все в большей мере рассеяние на фононах определяет длину свободного пробега.

Прокатка меди уменьшила λ с 1,95 до 0,45 при 5 К и с 1,25 до 0,9 Вт/м·К при 50 К. Прокатка алюминия при относительно высокой температуре 370 К уменьшила с 240 до 229 Вт/м·К. Никель, спрессованный до теоретической плотности, имел при 323 К λ = 80,0, а бездефектный – 88 Вт/м·К.

114

Таблица 5 Влияние степени протяжки на коэффициент теплопроводности

Слабое влияние дефектов при температурах, далеких от

T *, связано с тем, что при этих температурах длина свободно-

го побега электронов и фононов l ~ 1 Å, и чтобы существенно повлиять на их движение, рассеивающие центры должны быть на расстояниях ~ l. Это означает, что концентрация примесных

атомов должна быть ≥ 0,1, плотность дислокаций ≥ 10 14 cм 2 ,

размер субзерен ~ 10 Å, что уже близко к аморфному состоянию. Все это очень высокие плотности дефектов, означающие скорее переход материала в новое состояние, чем изменение исходного состояния (т.е. их нужно рассматривать не как дефекты старой структуры, а как новую структуру). Теплоемкость, скорость фононов (т.е. упругие свойства материала)

искорость электронов слабо зависят от дефектности решетки

ипотому, в соответствии с (82), можно ожидать, что от дефектности кристаллической решетки зависит слабо. Это подтверждают и другие экспериментальные данные. Так, в моно-

иполикристаллическом состоянии металлов Re, Nb, Mo отличается на величину, не превышающую 10–15 %.

Поскольку погрешность экспериментального измерения λ часто порядка 10–15 %, влияние этих дефектов на теплопроводность можно считать слабым.

115

5.3.Влияние пор и микротрещин на тепло-

иэлектропроводность

Обмен тепла между твердым телом и газом характеризуется коэффициентом теплопередачи α, по определению равным отношению плотности потока тепла через поверхность тела к характерной разности температур Т твердого тела и газа, т.е. α – размерная величина. В качестве безразмерной величины, характеризующей теплопередачу, пользуются числом Нуссельта:

где L – характерный размер поры, q – коэффициент тепло-

проводности газа. В уравнение конвективного движения газа в полости входят две безразмерные величины, число Прандтля:

где v – кинетическая вязкость газа, xq – коэффициент температуропроводности газа. И число Грассгрофа:

где – коэффициент объемного расширения газа, q – ускорение свободного падения.

Поэтому

Явный вид функции f(Gr, Pr) удается найти только для конвекции в неограниченном пространстве. Для замкнутых полостей эта зависимость исследовалась экспериментально. Оказалось, что эквивалентный коэффициент теплопроводности λэкв

116

Следовательно, конвективным компонентом теплопро-

приведены в табл. 6. Откуда следует, что конвективный перенос в порах порошкового материала возникнуть не может.

Теперь рассмотрим механизм переноса тепла в поре по механизму теплопроводности в газе. Коэффициент теплопроводности газа

117

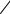
где В – константа, зависящая от свойств газа и характера взаимодействия молекулы газа с поверхностью твердого тела. При l < L, λq слабо зависит от давления газа р, так как при увеличе-

нии плотности g, за счет роста давления, пропорционально уменьшается длина свободного пробега l. Поэтому λq изменя-

ется примерно на 1 % при изменении ρ на 1 атм, в основном за

~ 1–30 Вт/м·К для диэлектриков, то в соответствии с вышеизложенным в широком диапазоне давлений λq « λ теплопровод-

ностью газа в порах можно пренебречь.

Теперь оценим величину лучистого теплопереноса в по-

где σ – постоянная Стефана – Больцмана, ε – степень черноты

стенок поры, R – радиус поры. Подставляя σ = 5,67·10 8 Вт/м·К и характерные для металлов λ = 30 Вт/м·К, ε = 0,3, при

R = 100 мкм получаем Т0 ~ 10 4 К. Если материал керамика, то

ε ~ 0,8, λ~ 1 Вт/м·К и при R = 100 мкм Т0 ~ 3000 К, т.е. ра-

диационный перенос тепла в порах можно не учитывать.

118

Итак, показано, что величина эффективного коэффициента теплопроводности определяется теплопереносом в твердой фазе, т.е. ее химическим составом и геометрией, например площадью межчастичных контактов в слабоспеченных материалах. Влияние дефектов кристаллического строения существенно только при низких температурах, а теплоперенос в порах, как правило, можно не учитывать.

5.4. Тепло- и электропроводность структурно-неоднородных сред в приближении сплошной среды

Наиболее яркой и очевидной отличительной особенностью структуры порошковых материалов является пористость. Влияние пористости на тепло- и электропроводность изучалось как экспериментальными, так и теоретическими методами. В приближении сплошной среды пористость, как правило, описывают общей пористостью и ищут зависимость эффективных коэффициентов тепло- и электропроводности λ* и σ*

от в виде

Поскольку форма, степень связности, распределение по размерам пор также влияют на то универсальной, справед-

ливой для всех материалов зависимости вида (97) не существует. Функция (97) должна обладать следующими очевидными свойствами: f (0) = 1, f (1) = 0, f ( ) ≤ 1. Вилка Фойгта – Ройсса

где λп – коэффициент эффективной теплопроводности пор. Из (98) видно, что функция λ* – выпуклая вниз, следовательно,

2 f / 2 0.

119

Из сопоставления с экспериментом следует, что m = 1,5 – 2. Если положить d λ* ~ λ* d то получим

Константа m' может быть выбрана так, что отличия значений λ*, вычисленных по (99) и (100), будут в пределах разбро-

са экспериментальных данных. Так, при m = 2 будет m' = 2,784 при максимальной относительной ошибке не более 0,07, при m = 1,5, m' = 2,250, = 0,10.

Обе зависимости (99) и (100), а для низкопористых систем и известные формулы Оделевского, удовлетворительно согласовываются с экспериментальными данными и могут быть рекомендованы для инженерных расчетов. Рекомендованные формулы неудовлетворительны только в одном отношении – они логически не обоснованы.

Список литературы к главе 5

1.Ашкрофт Н., Мермин Н. Физика твердого тела. – М.:

Мир, 1979.

2.Берман Р. Теплопроводность твердых тел. – М.: Мир, 1979. – 285 с.

3.Абрикосов А.А. Основы теории металлов. – М.: Наука, 1987. – 520 с.

4.Павлов П.В., Хохлов А.Ф. Физика твердого тела. – М.: Высшая школа, 1985. – 384 с.

5.Теплопроводность твердых тел: справочник / А.С. Охотин [и др.]. – М.: Энергоатомиздат, 1984. – 320 с.

6.Смитлз К. Дж. Металлы. – М.: Металлургия, 1980. –

446 с.

120