книги / Начала инженерного творчества

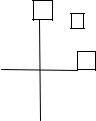
• нормировки – сумма квадратов элементов каждого столбца равна числу опытов:

N

∑ xij2 = N ; (3.17)

j=1

• ортогональности – сумма построчных произведений элементов двух любых столбцов равна нулю:

Ортогональность является важным свойством планов ПФЭ, поскольку оценка всех коэффициентов уравнения регрессии производится независимо друг от друга и факторы, имеющие незначимые коэффициенты, могут быть выведены из состава уравнения без повторного вычисления остальных коэффициентов уравнения регрессии;

• ротабельности, которая означает одинаковость предсказательной способности уравнений, полученных по планам ПФЭ по всем направлениям от начала координат, т.е. дисперсия предсказания зависит только от радиуса сферы, на которой

131

3.5.2. Метод наименьших квадратов. Оценка коэффициентов модели

Поскольку при проведении ПФЭ число опытов определяется величиной N = 2k, для идентификации четырехфакторной линейной модели, которая содержит 5 неизвестных коэффициентов, необходимо провести 16 опытов. В этом случае число уравнений, которые можно составить после проведения опытов по плану ПФЭ, превышает число неизвестных коэффициентов. С целью снятия переопределенности системы для вычисления коэффициентов полинома используют метод наименьших квадратов (МНК). Идея МНК состоит в том, что оценки коэффициентов линейного уравнения выбираются из условия минимизации ошибки аппроксимации ξi .

Пусть yi – действительное значение функции отклика, определяемое в i-м опыте, а y0i – значение, рассчитанное по формуле (3.19). Ошибка ξi определится как разность действитель-

ного и расчётного значений функции отклика ξi = yi – y0i.

Оценки коэффициентов уравнения регрессии определяются из условия

Предположим, что ошибки ξi в отдельных наблюдениях

имеют нормальное распределение с нулевым математическим ожиданием и одинаковой дисперсией Dу , не коррелированны

между собой и не зависят от значений факторов. Для простоты математических выкладок рассмотрим однофакторный эксперимент. Модель в этом случае имеет вид

Запишем условие (3.20) для рассматриваемого случая:

132

Минимум выражения (3.22) может быть достигнут за счет подбора коэффициентов b0 и b1. Это означает, что частные производные выражения (3.22) по неизвестным коэффициентам должны быть равны нулю.

Проведя несложные преобразования, получим систему линейных уравнений относительно неизвестных коэффициентов полинома:

Число уравнений в системе (3.24) равно числу двух искомых коэффициентов b0 и b1.

N

Исходя из свойств симметричности ∑ xij = 0 и нормиров-

i =1

N

ки ∑ xij2 = 0 систему (3.24) можно переписать как

i =1

Откуда могут быть получены оценки коэффициентов полинома

133

Формулы для определения оценок коэффициентов линейной модели в случае действия k факторов можно привести к единому виду, если в матрицу планирования ввести нулевой столбец, состоящий из верхних уровней нормированных факторов, т.е. +1 (см. табл. 33). Тогда выражение для j коэффициента примет вид

где j – номер коэффициента, стоящего при соответствующем факторе (j = 0, 1, ... k); i – номер опыта.

Таким образом, способ расчета коэффициентов модели в данном случае очень прост: для подсчета любого bj столбцу результатов эксперимента yi следует приписать знаки соответствующего столбца xj, сложить экспериментально найденные значения yi с этими знаками и результат разделить на число опытов матрицы планирования.

При ортогональном планировании формула для определения коэффициентов принимает вид

Поскольку коэффициенты регрессии рассчитывают по формуле (3.28) из результатов опытов, являющихся случайными величинами, то и сами коэффициенты являются случайными величинами. В общем случае эти коэффициенты имеют разные дисперсии и разную величину взаимной корреляции (различные ковариации и коэффициенты парной корреляции).

134

Коэффициент парной корреляции является мерой тесноты линейной связи между двумя случайными величинами. Его величина может меняться от 0 до ±1. Если коэффициент корреляции равен 0, связь между двумя случайными величинами либо вообще отсутствует, либо отлична от линейной. Если он равен 1, то связь является линейной. Наиболее важны случаи, промежуточные между полной корреляцией и отсутствием корреляции. Тогда коэффициент корреляции выражает ту долю вариации одной из переменных, которая связана с изменением значений другой. Естественно, чем ближе величина модуля коэффициента парной корреляции к 1, тем сильнее линейная связь, причем знак при коэффициенте парной корреляции указывает на направление связи: увеличение одной из переменных при положительной корреляции влечет за собой увеличение другой, а при отрицательной корреляции – уменьшение другой.

3.5.3. Оценка значимости коэффициентов модели

После нахождения оценок коэффициентов производится оценка их значимости, которая проводится путём сопоставле-

ния абсолютной величины коэффициента bj с его довери-

где tα – значение критерия Стьюдента, который берется из таблиц его распределения в зависимости от уровня значимости α (α = 0,01; 0,05; 0,1) и числа степеней свободы f1 = n0 – 1 (где n0 – число дублирующих опытов, обычно в центре плана). Для технических измерений α чаще всего принимается равным 0,05. Для меньших значений величины α доверительный интервал определения получается больше (табл. 34). sb j – сред-

неквадратичная ошибка в определении коэффициента регрес-

135

сии bj, которая определяется в зависимости от величины дис-

персии воспроизводимости Dy = s2y .

В случае равномерного дублирования опытов и числе дублирующих опытов в каждой строке плана n дисперсия коэффициентов определяется по формуле

Коэффициент считается статистически значимым, когда его абсолютная величина больше доверительного интервала его определения или равна ему.

Смысл последнего неравенства заключается в том, что абсолютная величина значимого коэффициента должна быть в tα раз больше, чем ошибка его определения.

Некоторые значения критерия Стьюдента tα приведены в табл. 34.

Статистическая незначимость коэффициента в уравнении (3.4) интерпретируется как отсутствие влияния соответствующего фактора. Если модель линейная и соответственно не-

136

значим линейный эффект, можно считать, что данный фактор в изученных интервалах его изменения на функцию отклика не влияет.

При ортогональном планировании статистически незначимые коэффициенты из модели могут быть исключены, при этом пересчет остальных коэффициентов не требуется.

3.5.4. Оценка адекватности модели

После оценивания коэффициентов модели проводится оценка адекватности модели, которая состоит в оценке однородности дисперсии воспроизводимости и дисперсии неадекватности с использованием критериев, приведенных в разд. 3.3.

Дисперсию неадекватности определяют по формуле

где yiм – значение у, определенное по модели для i-х условий эксперимента; yi – значение у, определенное в i-м опыте; f2 –

число степеней свободы определения дисперсии неадекватности.

где k′ – число найденных коэффициентов в модели.

При оценке адекватности модели по критерию Фишера оценивается отношение

ляемым при степени свободы дисперсии воспроизводимости f1 и степени свободы дисперсии неадекватности f2. Если

137

F ≤ Fт, то модель считается адекватной, в противном случае

модель неадекватна.

По сути дела модель считается адекватной, если погрешности расчета функции отклика y по модели не превышают погрешности ее экспериментального определения.

3.6. Матричный подход в теории планирования эксперимента

Математическим аппаратом, используемым для решения различных задач теории эксперимента, является линейная алгебра [20]. В матричной форме систему нормальных уравнений для отыскания оценок неизвестных коэффициентов после проведения опытов можно записать в виде

где [X ] – матрица условий эксперимента; [B] – матрица неизвестных коэффициентов; [Y ] – матрица результатов опытов.

b0b

[B]= ...1 , (3.37)

bk

138

Оценки коэффициентов [B], казалось, могли бы быть най-

однако для этого должна существовать мультикативно обратная матрица [X ]−1 , что возможно только в том случае, когда матрица [X ] является квадратной невырожденной матрицей. В общем случае в ТПЭ матрица [X ] является прямоугольной,

поскольку число экспериментов превышает число неизвестных коэффициентов.

Оценки коэффициентов [B] могут быть найдены на осно-

вании следующих матричных преобразований, снимающих переопределенность алгебраической системы и эквивалентных

139

Выражение (3.40) представляет собой систему нормальных уравнений МНК, записанную в матричной форме. Элементы матрицы [B] определяются из решения системы

Матрица [D]= [M ]−1 = ([X ]T [X ])−1 получила название ковариационной (или дисперсионной) матрицы. Ковариационная матрица [D] существует, если информационная матрица Фи-

шера квадратная, положительно определенная и невырожденная, а это выполняется, если N ≥ k +1 и хотя бы k +1 наблюдение (эксперимент) проведено в различных точках факторного пространства.

В общем случае ковариационная матрица имеет следующую структуру:

Матрица [X ]T [Y ] имеет вид

При ортогональном планировании, т.е. когда выполняется условие ортогональности (3.18), информационная матрица имеет диагональный вид

140