книги / Математические основы теории систем. Методы оптимизации

3.Находится область допустимых решений (область, где выполняются все ограничения).

4.Строится график целевой функции при каком-либо значении правой части:

Q = −2x1 − 4x2 = 0, x2 = − x1 . 2

5.График целевой функции перемещается параллельно его начальному положению в сторону уменьшения целевой функции до касания с границей области допустимых решений.

Отрезок прямой АВ является решением задачи линейного программирования.

6.В ответе записываются функция, граничные точки отрезка

изначение целевой функции на этом отрезке:

Способ 2

Пункты 1 – 3 выполняются аналогично описанным в способе 1. 4. Подсчитываются значения целевой функции во всех вершинах

допустимого многогранника:

няющий эти точки, является решением задачи.

21

2.4. Симплекс-метод решения задач линейного программирования

Симплекс-метод является универсальным методом решения ЗЛП [2]. Рассмотрим основные понятия симплекс-метода.

2.4.1. Канонический вид ЗЛП

Рассмотрим пример:

Q = 10 − x1 − x2 → min,

Канонический вид задачи должен удовлетворять следующим условиям:

1.Количество переменных (n) не меньше количества ограниче-

ний (m): n ≥ m;

2.Ограничения имеют вид равенств.

3.Среди n переменных имеются m переменных, которые удовлетворяют условию: коэффициент при этой переменной в одном ограничении равен единице, в остальных – нулю. Эти переменные на-

зывают базисными (x3, x4, x5 – базисные переменные), остальные (n – m) переменных называют свободными.

4.Правые части ограничений неотрицательны.

5. Целевая функция выражена через свободные переменные и минимизируется.

Каждому каноническому виду соответствует вершина допустимого многогранника.

2.4.2. Симплекс-таблица, соответствующая каноническому виду

Каждому каноническому виду поставлена в соответствие сим- плекс-таблица. Левый столбец таблицы – номера базисных переменных; верхняя строка таблицы – номера свободных переменных; пра-

22

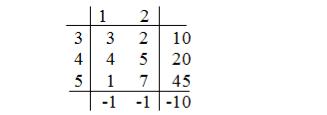
вый столбец – правые части ограничений; нижняя строка (кроме крайнего правого элемента) – коэффициенты целевой функции; элемент, стоящий справа в нижней строке, – значение (–Q0), где Q0 – свободный член целевой функции; внутреннее пространство таблицы – коэффициенты при свободных переменных (рис. 2.3):

Рис. 2.3. Симплекс-таблица для примера (2.4)

2.4.3. Нахождение координат вершины допустимого многогранника по каноническому виду (симплекс-таблице)

Задача линейного программирования может иметь столько канонических видов, сколько вершин у допустимого многогранника.

Для определения координат вершины допустимого многогранника свободные переменные приравниваются нулю, базисные переменные – правым частям ограничений. Целевая функция в данной вершине равна (–Q0).

Для вышеприведенной симплекс-таблицы

Для приведения задачи к каноническому виду добавим в первое ограничение переменную x3, во второе ограничение – переменную x4, целевую функцию помножим на –1:

23

где х3, x4 – базисные переменные, х1, x2 – свободные переменные. Этому каноническому виду соответствует вершина:

x1 = 0 , x2 = 0 , x3 = 10 , x4 = 20 , G = Q = 0 .

Составим таблицу коэффициентов при переменных в ограничениях:

Поделим коэффициенты второй строки таблицы на 2:

Как видим, для второй таблицы базисными являются переменные x2 , x3, а ограничения примут вид:

x1 + {x}3 = 10,

0,5x1 + x2 + 0,5x4 = 10.

Поскольку переменная x2 стала базисной, ее необходимо исключить из целевой функции:

G = − x1 − x2 = − x1 − (10 − 0,5x1 − 0,5x4 ) = −10 − 0,5x1 + 0,5{x}4 .

Соответствующая вершина имеет координаты:

x1 = 0 , х2 = 10 , x3 = 10 , x4 = 0 , G = −10 (Q = 10) .

2.4.4. Алгоритм решения ЗЛП с помощью симплекс-метода

Сущность симплекс-метода – это направленный перебор вершин допустимого многогранника и нахождение той вершины, где целевая функция минимальна.

24

Рассмотрим три алгоритма решения ЗЛП симплекс-методом. 1. ЗЛП приводится к каноническому виду.

Пусть требуется решить следующую задачу линейного программирования:

Q = Q0 + p3 x3 + p4 x4 → min ,

x1 + a13 x3 + a14 x4 = b1,

+ + =

x2 a23 x3 a24 x4 b2 ,

≥x1, x2 ,..., xn 0.

Данная задача уже приведена к каноническому виду (приведение ЗЛП к каноническому виду рассмотрено ниже). Составляется сим- плекс-таблица, соответствующая каноническому виду:

2.Находятся координаты вершины, соответствующей каноническому виду.

3.Анализируется целевая функция в вершине, т.е. выясняется, оптимальна ЦФ в данной вершине или нет:

Q = Q0 + p3 x3 + p4 x4 (например, Q = 10 − 4x3 + 5x4 ).

Если среди коэффициентов целевой функции имеется хотя бы один отрицательный, то целевая функция в этой вершине неоптимальна. Если все коэффициенты ЦФ неотрицательны, но имеется хотя бы один нулевой, то решение оптимально, но не единственно. Если все коэффициенты ЦФ положительны, то решение оптимально

иединственно.

4.Переход к другой вершине в случае неоптимальности. Для этого одна переменная из подмножества свободных меняется с одной переменной из подмножества базисных.

25

В качестве свободной переменной, переводимой в базисную, выбирается та, которая в наибольшей степени уменьшает целевую функцию (которая имеет максимальный по модулю отрицательный коэффициент целевой функции).

Столбец симплекс-таблицы, в котором находится свободная переменная, переводимая в базисную, называется разрешающим.

Пусть в рассматриваемой задаче р3 – максимальный по модулю отрицательный коэффициент целевой функции, тогда столбец а13, а23 – разрешающий, т.е. в новой симплекс-таблице x3 будет базисной переменной.

Для выбора базисной переменной, переводимой в свободную, находят отношения правых частей ограничений к положительным коэффициентам разрешающего столбца и выбирают минимальное отношение.

Строка симплекс-таблицы, в которой находится минимальное отношение, называется разрешающей. В этой строке расположена базисная переменная, переводимая в свободную.

Пусть

тогда строка (2, а23, а24, b2) – разрешающая.

Элемент, стоящий в разрешающей строке и разрешающем столбце, называется разрешающим (а23 – разрешающий элемент).

5.Выбранные свободные и базисные переменные (находящиеся

вразрешающих строке и столбце) меняются местами в симплекстаблице.

6.Пересчет коэффициентов в симплекс-таблице.

Поделим коэффициенты второго ограничения (разрешающая строка симплекс-таблицы) на разрешающий элемент:

26

Пересчитаем элементы первой строки симплекс-таблицы следующим образом: из коэффициентов первого ограничения вычтем соответствующие вновь полученные коэффициенты второго ограничения, домноженные на а13:

Пересчитаем целевую функцию (исключим из нее x3):

Введем следующие обозначения:

аi j – разрешающий элемент, стоящий в старой симплекстаблице;

âi j – элемент, стоящий на том же месте в новой симплекстаблице (пересчитанный разрешающий элемент);

27

аi j – разрешающая строка, j = 1…n; аij – разрешающий столбец, i = 1…m.

Тогда формулы для пересчета будут иметь следующий вид. Пересчитанный разрешающий элемент равен единице, деленной

на разрешающий элемент старой таблицы:

âi j = 1/ аi j .

Элементы новой разрешающей строки находят как произведение пересчитанного разрешающего элемента и соответствующих элементов старой разрешающей строки:

âi j = âi j аi j , j = 1…n.

Новый разрешающий столбец получают путем умножения элементов старого разрешающего столбца на пересчитанный разрешающий элемент, взятый с обратным знаком:

Остальные столбцы рассчитываются по формуле

âij = аij – âi j аij , i = 1…m , j = 1…n.

Для нахождения элементов нового столбца из старого столбца вычитают произведение элемента, уже стоящего в новом столбце, и старого разрешающего столбца.

7. Записывается решение ЗЛП в случае неотрицательности коэффициентов нижней строки симплекс-таблицы.

Пример 1

1. Приведем задачу к каноническому виду путем введения искусственных переменных:

28

Поскольку имеются отрицательные коэффициенты целевой функции, то вершина, которой соответствует симплекс-таблица, неоптимальна. Максимальный по модулю отрицательный коэффициент ЦФ – (–12), следовательно, второй столбец является разрешающим.

Для определения разрешающей стройки находим отношения правых частей ограничений к положительным коэффициентам разрешающего столбца и выбираем минимальное отношение:

220/2 = 110, 260/1 = 260,

640/5 = 128.

3. Составляем новую симплекс-таблицу: разрешающий элемент = 2; новый разрешающий элемент: 1:2 = 0,5;

новая разрешающая строка: 1 0,5 = 0,5; 220 0,5 = 110;

новый разрешающий столбец: 1 (–0,5) = –0,5; 5 (–0,5)= –2,5;

–12 (–0,5) = 6.

Элементы других столбцов:

29

Новая симплекс-таблица:

разрешающий столбец

Как видим, полученная вершина неоптимальна, и требуется перейти к следующей вершине.

4. Составляем следующую симплекс-таблицу:

Все коэффициенты целевой функции положительны, следовательно, найдено оптимальное и единственное решение задачи.

Ответ. координаты вершины: x1 = 60, x2 = 80, x3 = 0, x4 = 60, x5 = 0,

Gmin = –1440, Qmax = 1440.

Пример 2

Q = − x1 + x2 → min ,

Решение 1. Задача приводится к каноническому виду путем введения ис-

кусственных переменных:

30