
книги / Математические основы теории систем. Методы оптимизации
.pdf
Решение: |
|
||||
1. |
|
∂f |
= 2x1 – 7 – x2, |
a1 = 2 1 –7 –1 = –6. |
|
|
∂x1 |
||||
|
|
|
|
||
|
∂f |
|
= 2x2 – 4 – x1, |
a2 = 2 1 –4 –1 = –3. |
|
|
∂x2 |
||||
|
|
|
|||
2. x11 = x10 – α1, |
a1 = 1 + 6α1, |
||||
|
x21 = x20 – α1, |
a2 = 1 + 3α1. |
|||
3. f(x1, x2)= f(α1) = … = 27(α1)2 – 45α1 + 35.
Находим минимум f(α1): α11 = 5/6. x11 = 1 + 6α1 = 6,
x21 = 1 + 3α1 = 3,5. X1 (6; 3,5).
4. f (X1 ) − f (X0 ) = 16,75 > ε , следовательно, нужен еще шаг.
Пример 2
Найти безусловный экстремум методом наискорейшего спуска:
F(x1,x2) = 5x12 – 4x1x2 + 5x22 – x1 – x2; Х0 (1;1); ε = 0,01.
Тип экстремума минимум f(x1, x2). |
|
|||||
Решение: |
|
|
||||
1. |
|
∂f |
= 10x1 – 4x2, – 1, |
a1 |
= 10 1 – 4 1 – 1= 5, |
|
|
∂x1 |
|||||
|
|
|
|
|
||
|
∂f |
|
= –4x1 +10x1 – 1, |
a2 |
= –4 1 + 10 1 – 1 = 5. |
|
|
∂x2 |
|||||
|
|
|
|
|||
2.x11 = x10 – α1 a1 = 1 – 5α1, x21 = x20 – α1 a2 = 1 – 5α1.
3.f(x1, x2)= f(α1) = 50 – 300α1.
Находим минимум f(α1): α1 = 1/6.
x11 = 1 – 5α1 = 1/6, x21 = 1 – 5α1 = 1/6. Х1 (1/6; 1/6).
4. f(Х1) – f(Х0) = 4,167 > ε, следовательно, нужен еще шаг.
91
Задания для самостоятельной работы
Найти безусловный экстремум методами покоординатного и наискорейшего спусков:
1.f(x) = 7x12 + 2x1x2 + 5x22 + x1 – 10 x2,
Mo = (0; 0), ε = 0,01.
2.f(x) = 3x12 – 3x1x2 + 4x22 – 2x1 + x2,
Mo = (1; –1),
ε = 0,01.
3. f(x) = x12 + 4x1x2 + 17x22 + 5 x2, Mo = (1; –1),
ε = 0,01.
4. f(x) = 4x12 + 4x1x2 + 6x22 – 17 x1, Mo = (5; –1),
ε = 0,01.
5.f(x) = 2x12 – 2x1x2 + 3x22 + x1 – 3x2,
Mo = (1; 1), ε = 0,01.
6.f(x) = 10x12 + 3x1x2 + x22 + 10x2,
Mo = (0; –10),
ε = 0,01.
7. f(x) = x12 – 2x1x2 + 6x22 + x1 – x2, Mo = (–1; 1),
ε= 0,01.
3.5.Решение задач нелинейного программирования
сограничениями-равенствами
Чащевсегоиспользуется, когдаограничения имеют видравенств.
Метод неопределенных множителей Лагранжа
Некоторые сведения из математики. 1. Неявно заданная функция.
Говорят, что функция y(х) задана неявно, если эта функция входит в выражение F(x,y) = 0. Например, x2 + y2 – R2 = 0.
92

2. Производная неявно заданной функции.
∂F
dy = − ∂x . dx ∂F
∂y
3. Сложная функция.
Функция F является сложной, если она зависит от переменной у, а у, в свою очередь, зависит от переменной х:
F= f [ y(x)].
4.Производная сложной функции:
dF |
= |
∂f |
∂y . |
|
|
||
dx |
∂y ∂x |
||
5. Разновидность сложной функции: F = f [x, y(x)].
dF = ∂f + ∂f ∂y dx ∂x ∂y ∂x .
Вывод формул. Найдем решение для следующей задачи: Целевая функция F = f(x1, x2) → min,
ограничение: g(x1, x2) = 0, где f и g – нелинейные функции.
Выразим из g(x1, x2) = 0 переменную x2: x2= ϕ(x1).
Подставим x2 в целевую функцию: F = f [x1, ϕ(x1)]. Найдем экстремум функции одной переменной F = f [x1, ϕ(x1)]. Для этого найдем производную функции F и приравняем ее к нулю:
dF = ∂f + ∂f dϕ = 0. dx1 ∂x1 ∂ϕ dx1
Произведем обратную подстановку х2 вместо ϕ:
∂f + ∂f dx2 = 0,
∂x2 ∂x2 dx1
93

где dx2 – производная от неявно заданной функции х2. Воспользовав- dx1
шисьформулой производной отнеявнозаданной функции, получим:
|
|
|
|
|
|
|
|
|
∂g |
|
|
|
∂f |
− |
∂f |
|
|
|
∂x1 |
= |
0. |
||
|
|
|
|
|
|
|
∂g |
||||
|
∂x1 |
∂x2 |
|
|
|
||||||
|
∂x2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
Введем обозначение: |
|
|
|
|
|
|
|
|
|||
|
|
∂f |
|
1 |
|
= −λ. |
(3.18) |
||||
|
|
∂x2 |
|
|
|||||||
|
|
|
∂g |
|
|
|
|
||||
|
|
|
|
|
∂x2 |
|
|
|
|
||
В результате этих преобразований получена следующая система уравнений:
∂f + λ
∂x1
∂f + λ
∂x2
g(x1, x2
|
∂g |
= 0, |
|
|
|
|
|
|
|
||
∂x1 |
|
|
|||
|
∂g |
= 0, {домножили выражение (3.18) на |
∂f |
}, (3.19) |
|
|
∂x2 |
∂x2 |
|||
) = 0. |
|
|
|||
Введем функцию L = f(x1, x2) + λ g(x1, x2). Тогда ранее полученная система уравнений (3.19) – это частные производные функции L по всем переменным (x1, x2, λ), приравненные к нулю. Эта система уравнений и есть условие существования экстремума.
Здесь L – функция Лагранжа, λ – неопределенный множитель Лагранжа.
Таким образом, задача поиска условного экстремума с ограниче- ниями-равенствами сводится к задаче поиска безусловного экстремума функции Лагранжа.
Общая постановка задачи.
F = f (x1, x2 ,.., xn ) → min,
(3.20)
gi (x1, x2 ,..., xn ) = 0, i = 1,m.
94
Алгоритм метода:
1. Составляется функция Лагранжа:
m
L = f (x1, x2 ,.., xn ) + ∑λi gi (x1, x2 ,..., xn ),
i=1
где n – количество основных переменных, m – количество неопределенных множителей Лагранжа.
2. Находятся частные производные функции Лагранжа по переменным и приравниваются к нулю:
|
∂L |
|
|
|
|
|
|
|
= 0, j = 1,n, |
||||||
|
|
|
|||||
∂xj |
|||||||
|
|
|
|
|
|
||
|
∂L |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= 0, i = 1,m. |
||||||
|
∂λi |
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
3. Находится решение полученной системы и определяется вид экстремума.
Пример 1
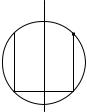
Найти стороны прямоугольника максимальной площади, вписанного в окружность радиус R.
|
|
Y |
||
Возьмем на окружности точку А(х, у), |
|
A |
||
|
|
|
||
тогда математическое описание задачи |
|
|
|
|
|
|
|
||
примет следующий вид: |
|
|
|
|
S = 4xy → max; |
|
X |
||
|
|
|
||
x2 + y2 – R2 = 0; x, y ≥ 0.
1. Составим функцию Лагранжа: L = f + λg = 4xy + λ (x2 + y2 – R2).
|
|
∂L = 4y + 2λx = 0, |
|||||||
|
|
||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
∂L |
|
|
|
|
|
|
|
2. |
|
∂y |
= 4y + 2λy = 0, |
||||||
|
|
∂L |
= x |
2 |
+ y |
2 |
− R |
2 |
= 0. |
|
|
∂λ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
95
Решим систему уравнений.
3. Из первого уравнения: y = − λx . 2
Подставляем во второе уравнение: 4x – λ2x = 0; x(4 – λ2) = 0;
x = 0, λ1 = 2, λ2 = –2.
Корень х =0 не удовлетворяет условиям задачи. По аналогичной причине отбрасываем корень λ1:
λ1 = 2; y = – λx/2 = – 2х/2 = –x < 0.
λ2 = –2; y = – λx/2 = x. 4. Оставляем корень λ1 = 2.
Подставив x = y втретьеуравнениесистемы, получаем x = y = R . 2
Пример 2
Найти точку на прямой 2x1 + 3x2 = 1, квадрат расстояния от которой до точки (1; 2) минимален.
Решение:
1. Составляем целевую функцию и ограничения:
(x1 – 1)2 + (x2 – 2)2→ min,
2x1 + 3x2 – 1= 0, где x1, x2 – точки, принадлежащие прямой, 2x1 + 3x2 = 1.
2.Составляем функцию Лагранжа:
L = (x1–1)2 + (x2–2)2 + λ (2x1 + 3x2 – 1).
3.Находим частные производные по переменным функции Ла-
гранжа и приравниваем их к нулю.
∂L |
|
= 2(x1 |
− 1) + 2λ = 0, |
|
|
|
|
||
∂x1 |
||||
|
∂L |
|
= 2(x2 |
− 2) + 3λ = 0. |
|
∂x |
|
||
|
|
|
||
|
2 |
|
|
|
4. Решается полученная система уравнений.
x1 − 1+ λ = 0,− + λ =
2x2 4 3 0,+ =
2x1 3x2 1,
2x2 − 4 + 3λ − 3x1 + 3 − 3λ = 0.
96

3x2 + 2x1 = 1,2x2 − 3x1 = 1,
2x2 − 3x1 = 4,5x2 + 3x1 = 1+ 1,5. 6,5x2 = 2,5.
x1 |
= |
(1− 3x2 ) |
= − |
1 |
, |
||
|
|
|
|
||||
|
2 |
13 |
|||||
x2 |
= − |
5 |
. |
|
|
|
|
|
|
|
|
||||
|
13 |
|
|
|
|||
Ответ: − 1 ; 5 . 13 13
Задание для самостоятельной работы
Найти условный экстремум методом неопределенного линейного программирования.
1. z = x1·x22 x33 |
2. z = x1 – 2x2 +2x3 |
при x1+x2+ x3 = 12 |
при x12+ x22+x3 2 = 9 |
3. z = x12+ x22 |
4. z = x12+ x22 + x32 →min |
при x1 + x2 = 5 |
при x1+x2+ x3 ≤ 12 |
x1, x2 , x3 ≥ 0 |
|
5. z = x1·x2·x3 |
6. z = 2x1 + 3x22 +x32 |
при x1+x2+ x3 = 5 |
при x1+ x2+x3 = 8 |
x1·x2 + x2·x3 + x3·x1 = 8 |
x1, x2, x3 ≥0 |
7. z = x12 + x22 +x3 |
8. z = x1·x2 + x2·x3 |
при x1+ x2+x3 2 = 4 |
при x1+ x2 = 4 |
2x1 – 3x2 = 12 |
x2 + x3 = 4 |
9. z = x1·x2·x3 |
10. z = 6 – 4x1 – 3x2 |
при 2x1·x2+x2·x3 = 12 |
при x12+ x2 = 1 |
2x1 – x2 = 8 |
|
11. z = 4x1 + x12 + 8x2 + x22 |
12. z = x12·x2 + x22·x1 + x1·x2·x3 + x32 →min |
при x1+ x2 = 180 |
при x1+x2+ x3 ≤ 15 |
x1, x2 ≥0 |
x1, x2 , x3 ≥ 0 |
|
97 |

13. z = x1·x2·x3·x4 |
14. z = x1·x2·x3 |
при x1+ x2 + x3 + x4 = 4 |
при x1+ x2 + x3 ≤ 6 |
x1, x2 , x3, x4 ≥ 0 |
x1·x2 + x1·x3+ x2·x3 ≤ 8 |
15. z = x1·x2 + x1·x3 + x2·x3 →min |
16. z = x1·x2·x3 |
при x1+x2+ x3 ≤ 4 |
при x1+ x2 + x3 = 6 |
|
x1·x2 + x1·x3+ x2·x3 = 12 |
17. z = x12·x23· x34→max |
18. z = x1 – 2x2 + 2x3→max |
при x1+ x2+ x3 =18 |
при x12+ x22 + x32 ≤ 9 |
3.6. Задачи квадратичного программирования
Постановка задачи:
1. F = f(x1, x2, … xn) → max,
целевая функция – многочлен второго порядка.
2. gi(x1, x2,…xn) ≤ bi, i = 1, m – ограничения линейные.
Если ограничения имеют вид ≥, то они приводятся к нужному виду путем домножения на –1.
3. x1, x2,…xn ≥ 0.
Квадратичная функция имеет только один экстремум. Задачи квадратичного программирования решаются с помощью теории Ку- на–Таккера.
Алгоритм решения:
1. Составляется функция Лагранжа:
m
L = f (x1, x2 ,..., xn ) + ∑λi (bi − gi (x1, x2 ,..., xn )),
i=1
где λi – где неопределенные множители Лагранжа. 2. Составляются условия Куна–Таккера:
|
∂L |
|
≤ 0, |
j = |
|
|
|
|
, |
|
|
|||||
1,n |
||||||||||||||||
|
|
|||||||||||||||
∂xj |
|
∂L |
|
|
|
|
|
|
|
|
|
|
|
|||
xj |
|
= 0, |
j = |
|
|
|
, |
|
|
|||||||
1,n |
||||||||||||||||
|
|
|||||||||||||||
|
|
∂xj |
|
|
|
|
|
|
|
|
|
|||||
|
∂L |
≥ 0, |
i = |
|
|
, |
||||||||||
1,m |
||||||||||||||||
|
||||||||||||||||
∂λi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
λi |
|
|
∂L |
= 0, |
i = |
|
. |
|||||||||
|
1,m |
|||||||||||||||
|
|
|
||||||||||||||
|
∂λi |
|
|
|
|
|
|
|
|
|
||||||
(3.21)
(3.22)
98

В условиях Куна–Таккера ограничения-неравенства заменяются равенствами путем введения искусственных переменных:
|
∂L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ vj |
= 0, |
j = 1,n, |
|||||||||||
|
|
|
||||||||||||
∂xj |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0, |
(*) |
j = 1,n, |
|||||||||
xj vj |
||||||||||||||
|
∂L |
|
|
|
|
|
(3.23) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
− wi |
= 0, |
i = 1,m, |
|||||||||||
|
|
|
||||||||||||
∂λi |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0, |
(**) |
i = 1,m, |
||||||||
λi wi |
||||||||||||||
3. Данная задача решается методами линейного программирования, например методом искусственного базиса. Особенность решения – в процессе перехода от одной симплекс-таблицы к другой должна быть хотя бы одна переменная из ограничений (*) и (**) свободной.
Если вид целевой функции другой (min), то ограничения следует привести к виду ≥. Тогда условия Куна–Таккера будут выглядеть следующим образом:
|
∂L |
≥ 0, |
||||
|
|
|||||
∂xj |
|
|
|
|||
|
∂L |
|
|
|||
xj |
= 0, |
|||||
|
||||||
|
∂xj |
|||||
∂L |
≤ 0, |
|||||
|
|
|
||||
∂λi |
||||||
|
|
|
||||
|
|
|
|
|||
λi |
|
∂L |
= 0, |
|||
|
|
|||||
|
∂λi |
|||||
Пример
j = 1,n,
j = 1,n,
(3.24)
i= 1,m.
i= 1,m.
Решить задачу квадратичного программирования:
x1 |
+ x2 ≤ 2, |
x1 |
+ 2x2 ≤ 2, |
|
, x2 ≥ 0. |
x1 |
99
Решение 1. Поскольку целевая функция минимизируется, то ограничения
нужно привести к виду ≥:
x1 |
− x2 ≥ −2, |
x1 |
− 2x2 ≥ −2. |
2. Составляем функцию Лагранжа:
f (x1, x2 ) = x12 + 2x22 − 2x1x2 − 2x1 − 6x2 +
+ λ1 (−2 + x1 + x2 ) + λ2 (−2 − x1 + 2x2 ).
3. Составим систему Куна–Таккера:
|
∂L |
|
|
|
|
= 2x1 − 2x2 − 2 + λ1 − λ2 ≥ 0, |
|||||
|
|||||||||||
∂x1 |
|
|
|
|
|
|
|
|
|
||
|
∂L |
|
|
|
= 4x2 − 2x1 − 6 + λ1 + 2λ2 ≥ 0, |
||||||
|
|
|
|||||||||
∂x2 |
|
|
|
|
|
|
|
|
|
||
|
∂L |
|
|
|
|
= −2 + x1 + x2 ≤ 0, |
|||||
|
|
|
|
|
|
|
|||||
∂λ1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
∂L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −2 − x1 + 2x2 ≤ 0, |
||||
|
|
|
|
|
|
||||||
|
∂λ2 |
||||||||||
|
|
|
|
|
|
∂L |
|
|
|
|
|
x1 |
|
|
|
= 0, |
|||||||
|
|
|
|
||||||||
|
|
|
∂x2 |
||||||||
|
|
|
|
|
|
∂L |
|
|
|
||
x2 |
|
= 0, |
|||||||||
|
|
||||||||||
|
|
|
|
|
∂x2 |
||||||
|
|
|
|
|
|||||||
λ1 |
|
|
|
|
∂L |
= 0, |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
∂λ1 |
||||||
λ2 |
|
|
|
|
∂L |
= 0. |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
∂λ2 |
|||||
100
