
книги / Математика. Дифференциальные уравнения
.pdf
|
|
Основные формулы |
|
Определения и замечания |
|
|||
|
y(n) = f (x) |
|
(3.6) – нахождение частного реше- |
|||||
|
|
(x0 ) = y0 |
|
ния уравнения (3.4) при заданных |
||||
|
y |
|
начальных условиях (задача |
Ко- |
||||
|
|
|
|
|
|
ши). |
|
|
5. y′(x0 ) = y0′ |
|
|
|
|||||
|
. . . . . . . . . . |
|
Замечание. |
|
|
|||
|
(3.6) |
При отыскании частного решения |
||||||
|
|
(n−1) |
|
(n−1) |
|
уравнений высших порядков нет не- |
||
|
|
(x0 ) |
|
|||||
|
y |
|
= y0 |
|
обходимости сначала находить об- |
|||
|
|
|
|
|
|
щее решение, а лишь затем опреде- |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
лять значения всех постоянных. |
||
|
|
|
|
|
|
Можно, и это лучше, определять |
||
|
|
|
|
|
|
значение каждой постоянной не- |
||
|
|
|
|
|
|
медленно после того, как она появ- |
||
|
|
|
|
|
|
ляется в процессе решения. |
|
|
6. |
F ( x, y′, y′′) = 0 |
(3.7) |
Дифференциальное уравнение (3.7) |
|||||
|
|
|
|
|
|
явно не содержит искомую функ- |
||
y′ = p (x) |
|
(3.8) |
цию y. |
|
|
|||
|
Следует запомнить: |
|
||||||
F (x, p, p′) = 0 |
|
|
||||||
(3.9) |
выполняя подстановку (3.8), преоб- |
|||||||
|
|
|
|
|
|
разуем уравнение (3.7) к уравнению |
||
|
|
|
|
|
|
первого порядка |
относительно |
p |
|
|
|
|
|
|
(3.9). |
|
|
|
|
|
|
|
|
Замечание. |
|
|
|
|
|
|
|
|
Так как y′ = p (x), |
то y′′ = p′(x). |
|
|
|
|
|
|
||||
7. |
p = ϕ(x,C1 ) |
(3.10) |
Решение уравнения (3.9). |
|
||||
y = ∫ϕ(x,C1 )dx +C2 |
(3.11) |
Искомое общее решение уравнения |
||||||
|
|
|
|
|
|
(3.7) получим интегрированием ра- |
||
|
|
|
|
|
|
венства y′ = p (x). |
|
|
|
|
|
|
|||||
8. |
F ( y, y′, y′′) = 0 |
(3.12) |
Дифференциальное уравнение (3.12) |
|||||
y′ = p ( y) |
|
|
явно не содержит x . |
|
||||
|
(3.13) |
Замечание. |
|
|
||||
|
|
|
|
|
|
Поскольку y′ = p ( y) , то |
|
|
F ( y, p, pp′) = 0 |
(3.14) |
y′′ = p′( y) y′ = p′p. |
|
|||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
61 |

|
|
Основные формулы |
|
Определения и замечания |
||
|
|
|
|
|
Следует запомнить: |
|
|
|
|
|
|
выполняя подстановку (3.13), пре- |
|
|
|
|
|
|
образуем уравнение (3.12) к уравне- |
|
|
|
|
|
|
нию первого порядка относительно р |
|
|
|
|
|
|
(3.14). |
|
|
|
|
||||
9. p = ϕ( y,C1 ) |
(3.15) |
Решение уравнения (3.14) |
||||
y′ = p = ϕ( y,C1 ) , т.е. |
|
Замечание. |
|
|||
|
Искомый общий интеграл получим |
|||||
|
dy |
|
= x +C2 |
(3.16) |
из уравнения с разделяющимися пе- |
|
∫ ϕ( y,C1 ) |
ременными. |
|
||||
|
|
|
||||
10. |
|
|
|
Замечание. |
|
|
|
|
|
|
|
В случаях (3.7) и (3.12) мы заменяли |
|
|
|
|
|
|
производную y′ |
новой вспомога- |
|
|
|
|
|
тельной функцией и приходили, та- |
|
|
|
|
|
|
ким образом, к уравнению первого |
|
|
|
|
|
|
порядка. |
|
y′′ = f ( y′) |
(3.17) |
Если уравнение |
имеет вид (3.17), |
|||
|
|
|
|
|
т.е. если оно одновременно отно- |
|
|
|
|
|
|
сится и к типу (3.7), и к типу (3.12), |
|
|
|
|
|
|
то следует выбрать тот ход реше- |
|
|
|
|
|
|
ния, который окажется более удоб- |
|
|
|
|
|
|
ным. |
|
Задачи
Задача 1. Найти общее решение уравнения
y′′′= e3x
и выделить решение, удовлетворяющее начальным условиям: y (0) = 0, y′(0) =1, y′′(0) =1.
Решение
Интегрируем последовательно данное уравнение:
y′′= ∫e3x dx +C1 = 13 e3x +C1 ,
62
y′= |
1 e3xdx + |
∫ |
C dx +C = 1 e3x +C x +C , |
|
|||||||||||||||||||||
|
∫ 3 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
9 |
|
|
1 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x2 |
|
|
||
y = ∫ 9 e3xdx + ∫C1xdx + |
∫C2dx +C3 = |
|
|
|
e3x +C1 |
|
|
+C2 x +C3 |
– общее |
||||||||||||||||
27 |
2 |
||||||||||||||||||||||||
решение уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем решение, удовлетворяющее поставленным начальным |
|||||||||||||||||||||||||
условиям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y (0) = 0 : |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
+C3 = 0, |
|
|
|||||||||||||
|
|
|
27 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y′(0) |
= |
1: |
+C2 =1, |
|
|
|
||||||||||||||||
|
|
|
9 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
y′′(0) |
=1: |
1 |
+C1 =1. |
|
|
|
||||||||||||||||
|
|
|
3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Получим: C = 2 |
, |
C |
|
= |
8 , |
C = − |
1 |
, |
поэтому искомым реше- |
||||||||||||||||
2 |
|
||||||||||||||||||||||||
|
1 |
3 |
|
|
|
|
9 |
3 |
|
|
|
|
|
27 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нием будет: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
1 |
|
e3x |
+ |
x2 |
|
+ |
8 x − |
1 |
. |
|
|
(*) |
|||||||||
|
|
|
27 |
|
|
27 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
9 |
|
|
|
|
|
|
||||||
Если ставить целью только решение задачи Коши, то начальным условиям можно удовлетворять постепенно, в процессе последовательного интегрирования данного уравнения (замечание гл. III, §1, п. 5).
Интегрируем данное уравнение:
y′′ = 13 e3x +C1 .
Полагая здесь x = 0, y′′ =1, находим C1 = 23 ,
откуда
y′′= 13 e3x + 23 .
63

Интегрируем еще раз:
y′= 19 e3x + 23 x +C2 .
Полагая здесь x = 0 , y′=1 , находим C2 = 89 .
Тогда y′= |
1 e3x + |
2 x + |
8 . |
|
|
|
|
||
|
9 |
3 |
|
9 |
|
|
|
|
|
Интегрируем еще раз: |
|
|
|
|
|
|
|||
|
|
y = |
1 |
e3x + |
x2 |
+ |
8 x +C . |
||
|
|
|
|
||||||
|
|
27 |
|
3 |
|
9 |
3 |
||
|
|
|
|
|
|||||
Подставив вместо x и y их начальные значения x0 = 0, y0 = 0,
найдем C3 = − 271 , так что снова получим искомое решение в виде (*).
Задача 2. Решить уравнение
y′′+ yx′ = x .
Решение
В уравнение явно не входит y , следовательно, выполняем за-
мену (3.8):
y′= p(x) , y′′= p′(x) .
Приходим к уравнению первого порядка:
p′+ xp = x ,
которое оказывается линейным (гл. I, §4, п.1). Решив его, найдем
p = x2 + C1 . 3 x
64
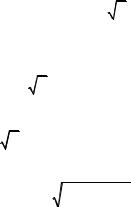
Тогда y′= |
x2 |
+ |
C |
y = |
x3 |
+C ln |
|
+C |
|
|
|
|
1 |
и |
|
x |
2 |
. |
|||||
|
|
|
|||||||||
|
3 |
|
x |
|
9 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
||||
Задача 3. Решить уравнение
2 yy′′+ y′2 = 0 .
Решение
В уравнение явно не входит x, следовательно, выполняем за-
мену (3.13):
y′= p( y) , y′′ = p′p .
Получим 2 yp′p + p2 = 0. Это уравнение первого порядка с разделяющимися переменными. Приводя его к виду
|
|
|
|
|
|
dp |
= − dy |
|
|
|
||||
|
|
|
|
|
|
p |
|
2 y |
|
|
|
|||
и интегрируя, получим: |
|
|
|
|
|
|
|
|
|
|
||||
ln |
|
p |
|
= −1 ln |
|
y |
|
+ln C |
или p = |
C1 |
. |
|||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
1 |
|
|
y |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как p = y′, имеем: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dy |
= |
C1 |
. |
|||||
|
|
|
|
|
|
dx |
|
|||||||
|
|
|
|
|
|
|
y |
|
|
|
||||
Определив y из уравнения |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
ydy =C1dx , |
|||||
придем к искомому решению: |
|
|
|
|
|
|
||||||||
3 |
|
|
|
|
|
или y = 3 (C1x +C2 )2 . |
||||||||
y2 =C1x +C2 |
|
|||||||||||||
Замечание. При сокращении на |
p было потеряно решение |
|||||||||||||
уравнения p = y′= 0 , т.е. y = const . В данном случае оно получается из общего решения при C1 = 0.
65

§2. Линейные уравнения с постоянными коэффициентами
Основные формулы |
Определения |
|
и замечания |
||
|
|
|
|
( |
|
) |
|
( |
) |
|
|
( |
n−2 |
) |
|
|
(3.18) |
(3.18) |
– |
линейное |
одно- |
|||
1. |
|
y |
|
n |
|
+a1 y |
|
n−1 |
+a2 y |
|
|
+... + |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
родное уравнение n-го по- |
|||||||||||||
+an−1 y′+an y = 0 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
рядка. |
|
|
|
|
дейст- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 , a2 ,..., an−1 , an |
– |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вительные постоянные. |
|
|||||
2. |
kn +a1kn−1 +a2 kn−2 +... + |
|
(3.19) |
Характеристическое урав- |
|||||||||||||||||||
+an−1k +an = 0 |
|
|
|
|
|
|
|
|
нение |
|
для |
уравнения |
|||||||||||
|
|
|
|
|
|
|
|
(3.18). |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. |
|
|
полу- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение |
(3.19) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чим, заменив y(n) |
на |
kn , |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(n−1) |
на kn−1 … y′ на k , |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y на k0 |
=1. |
|
|
|
|
|
3. |
|
|
= C1 y1 +C2 y2 +... +Cn yn |
|
(3.20) (3.20) |
– общее решение |
|||||||||||||||||
|
y |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения (3.18). |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следует запомнить: |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если y1 , y2 ,..., yn – |
реше- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния |
уравнения |
|
(3.18), |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
причем |
попарно |
линейно |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
независимые, то |
общим |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решением |
уравнения |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.18) является их линей- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ная комбинация (3.20). |
|
|||||
4. |
|
|
= C ek1x |
+C |
ek2 x +... +C |
ekn x |
(3.21) |
Общее |
решение |
уравне- |
|||||||||||||
|
y |
||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
n |
|
|
ния (3.18) при условии, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что корни |
k1, k2 ,..., kn |
– |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действительные и различ- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ные. |
|
|
|
|
|
|
66

Основные формулы |
Определения |
|
и замечания |
||
|
5. |
y |
= ek1x , y |
2 |
= xek1x ,..., y |
m |
= xm−1ek1x |
(3.22) |
Если |
k1 |
есть |
действи- |
||||
|
1 |
|
|
|
|
|
|
тельный |
корень |
уравне- |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ния |
(3.19) |
кратности |
m, |
||
|
|
|
|
|
|
|
|
|
|
то ему |
соответствует |
m |
|||
|
|
|
|
|
|
|
|
|
|
линейно независимых ре- |
|||||
|
|
|
|
|
|
|
|
|
|
шений уравнения (3.18). |
|||||
|
|
|
|
|
|
|
|
|
|
Следует запомнить: |
|
||||
|
|
|
|
|
|
|
|
|
|
в формуле общего реше- |
|||||
|
|
|
|
|
|
|
|
|
|
ния |
(3.21) |
соответствую- |
|||
ek1x (C1 +C2 x +C3 x2 +... +Cm xm−1 ) |
|
щие m члены заменяются |
|||||||||||||
(3.23) |
слагаемым (3.23). |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Замечание. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Общая сумма кратностей |
|||||
|
|
|
|
|
|
|
|
|
|
всех корней должна рав- |
|||||
|
|
|
|
|
|
|
|
|
|
няться степени характери- |
|||||
|
|
|
|
|
|
|
|
|
|
стического |
уравнения |
n; |
|||
|
|
|
|
|
|
|
|
|
|
поэтому число всех част- |
|||||
|
|
|
|
|
|
|
|
|
|
ных решений будет в точ- |
|||||
|
|
|
|
|
|
|
|
|
|
ности совпадать с поряд- |
|||||
|
|
|
|
|
|
|
|
|
|
ком уравнения. |
|
|
|||
6. |
y1 = eαx cosβx, y2 = eαx sin βx, |
(3.24) |
Если |
α±iβ – пара ком- |
|||||||||||
y |
= xeαx cosβx, y |
4 |
= xeαx sin βx,..., |
|
плексных корней уравне- |
||||||||||
3 |
|
|
|
|
|
|
|
|
ния |
(3.19) |
кратности |
m , |
|||
y2m−1 = xm−1eαx cosβx, y2m = xm−1eαx sin βx |
|
||||||||||||||
|
то ей соответствует |
2m |
|||||||||||||
eαx (C1 +C2 x |
+... |
+Cm xm−1 )cosβx + |
|
линейно независимых ре- |
|||||||||||
|
|
|
|
|
|
|
|
|
(3.25) |
шений уравнения (3.18). |
|||||
(Cm+1 +Cm+2 x +... +C2m xm−1 )sin βx |
Следует запомнить: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
в формуле общего реше- |
|||||
|
|
|
|
|
|
|
|
|
|
ния |
(3.21) |
соответствую- |
|||
|
|
|
|
|
|
|
|
|
|
щие m пар членов заме- |
|||||
|
|
|
|
|
|
|
|
|
|
няются слагаемым (3.25). |
|||||
7. |
y(n) +a1 y(n−1) +a2 y(n−2) +...an−1 y′+ |
(3.26) |
(3.26) – линейное неодно- |
||||||||||||
+an y = f (x) |
|
|
|
|
|
родное уравнение n-го |
|||||||||
|
|
|
|
|
|
порядка |
с |
постоянными |
|||||||
|
|
|
|
|
|
|
|
|
|
коэффициентами. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |

|
|
|
Основные формулы |
|
|
|
|
Определения |
|
|
||
|
|
|
|
|
|
|
|
и замечания |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
8. y = |
|
+ y* |
|
(3.27) Общее |
решение |
у |
= |
|||||
y |
|
|||||||||||
|
|
|
|
= y (x,C1,C2 ,...,Cn ) |
урав- |
|||||||
|
|
|
|
нения (3.26) получается из |
||||||||
|
|
|
|
суммы |
общего |
решения |
||||||
|
|
|
|
|
|
= |
|
(x,C1 ,C2 ,...,Cn ) |
со- |
|||
|
|
|
|
|
y |
y |
||||||
|
|
|
|
ответствующего однород- |
||||||||
|
|
|
|
ного уравнения (3.18) и |
||||||||
|
|
|
|
частного решения |
y* |
не- |
||||||
|
|
|
|
однородного |
уравнения |
|||||||
|
|
|
|
(3.27). |
|
|
|
|
||||
|
|
|
|
Замечание 1. |
|
|
|
|||||
Нахождение общего решения однородного линейного уравнения (3.18) было только что рассмот-
рено (пп. 2–6).
Замечание 2.
При отыскании частного решения неоднородного уравнения (3.26) рассматривают случаи, когда правая часть имеет специальный вид (см. гл II, §3) и
когда f (x) – любая, то
следует применить метод вариации произвольных постоянных (см. гл. II, §4).
Задачи
Задача 1. Найти общие решения уравнений:
а) y′′′−5y′′+6 y′= 0, б) y′′′−2 y′′+ 4 y′−8y = 0, в) yV − y′′′= 0.
Решение
а) Рассмотрим уравнение
y′′′−5y′′+6 y′= 0 .
68
Здесь характеристическое уравнение k3 −5k2 +6k = 0 , k (k2 −5k +6) = 0
имеет корни k = 0 , k |
2 |
= 2 , k |
3 |
=3 . Поэтому, |
y = e0 x =1, |
y |
2 |
= e2 x , |
1 |
|
|
1 |
|
|
y3 = e3x .
Тогда общее решение заданного дифференциального уравнения запишется так:
|
|
|
|
|
|
y |
=C +C |
e2 x +C e3x . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
|
|
|
|
б) Характеристическое уравнение для уравнения |
||||||||||||||||||
|
|
|
|
|
|
y′′′−2 y′′+ 4 y′−8y = 0 |
||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
k3 −2k2 + 4k −8 = 0 , |
||||||||||||||
|
|
|
|
|
k2 (k −2) + 4(k −2) = 0 , |
|||||||||||||||
|
|
|
|
|
|
|
(k −2)(k2 + 4) = 0 . |
|||||||||||||
|
|
Один корень действительный k1 = 2 и два чисто мнимых корня |
||||||||||||||||||
k |
2,3 |
= ±2i . Поэтому y = e2 x |
, |
y |
2 |
= cos 2x , |
y |
=sin 2x и |
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
=C e2 x |
+C |
|
cos 2x +C sin 2x . |
||||||||||||
|
|
|
|
y |
2 |
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
в) Для уравнения yV − y′′′= 0 имеем: |
) |
|
||||||||||||||||
|
|
|
|
|
k5 −k3 |
= 0 , k3 |
( |
|
|
= 0 . |
||||||||||
|
|
|
|
|
|
k2 −1 |
||||||||||||||
|
|
Здесь, k1,2,3 |
= 0 , k4,5 = ±1 . Поэтому: |
|
|
|
||||||||||||||
|
|
y = e0 x =1, y |
2 |
= x , y = x2 , y |
4 |
= ex , y = e−x |
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
y =C +C |
2 |
x +C x2 |
+C |
ex +C e−x . |
|||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
69 |

Задача 2. Указать вид частных решений для данных неоднородных уравнений (коэффициент не определять):
а) y′′′− y′= ex sin x + 2x2 , б) yIV + 2 y′′+ y =5sin x − xcos x .
Решение
а) Найдем общее решение соответствующего однородного уравнения:
y′′′− y′= 0 ,
k3 −k = 0 , k1 = 0 , k2 =1, k3 = −1 , y =C1 +C2ex +C3e−x .
Для нахождения частного решения неоднородного уравнения рассмотрим два вспомогательных уравнения:
y′′′− y′= ex sin x , |
(*) |
y′′′− y′= 2x2 |
(**) |
и находим для каждого из них частные решения y * |
и y *. |
1 |
2 |
Частное решение уравнения (*) ищем в виде y1* = ex ( Asin x + B cos x) ,
так как α ±iβ =1±i не является корнем характеристического уравнения, а частное решение уравнения (**) – в виде
y2* =(Cx2 + Dx + E) x ,
так как α = 0 – корень характеристического уравнения, кратности
λ =1.
Тогда
y* = y1* + y2* = ex ( Asin x + B cos x) +(Cx2 + Dx + E) x.
70
