31. Достаточные условия экстремума.

Точка, в которой частные производные первого порядка функции равны нулю, т. е. , , называется стационарной точкой функции.

В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию . Для неё точка 0(0,0) является критической (в ней и обращаются в ноль). Однако экстремума в ней функция не имеет, т. к. в достаточно малой окрестности точки 0(0,0) найдутся точки, для которых (точки I и III четвертей) и (точки II и IV четвертей).

Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.

Теорема 2 (достаточное условие экстремума). Пусть в стационарной точке и некоторой её окрестности функция имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке значения , , . Обозначим

 

 

Тогда:

1. если , то функция в точке имеет экстремум: максимум, если A < 0, минимум, если A > 0;

2. если , то функция в точке экстремума не имеет.

В случае экстремум в точке может быть, может не быть. Необходимы дополнительные исследования. Примем без доказательства.

32. Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке

Говорят, что функция  , определенная на промежутке Х, достигает на нем своего наибольшего (наименьшего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из Х выполняется неравенство  .

Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции  на отрезке  :

1. найти ;

2. найти точки, в которых  или  не существует, и отобрать из них те, что лежат внутри отрезка ;

3. вычислить значения функции  в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции  на отрезке  , которые можно обозначить так: .

33 . График дифференцируемой функции у = f(x)называется выпуклым внизна интервале (a; b), если он расположен выше любой ее касатель­ной на этом интервале. График функции у = f(x) называется выпуклым вверхна интервале (a; b), если он расположен ниже любой ее касательной на этом интервале.

Точка графика непрерывной функции у = f(x),отделяющая его части разной вы­пуклости, называется точкой перегиба.

На рисунке 14 кривая у = f(x)выпу­кла вверх в интервале (a; c), выпукла вниз в интервале (с; b), точка М(с; f(с)) — точка перегиба.

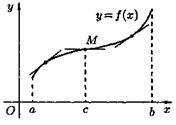
Рис. 14.

Теорема.Если функция у = f(x) во всех точках интервала

(a; b) имеет от­рицательную вторую производную, т. е. f "(x) <0, то график функции в этом ин­тервале выпуклый вверх. Если же f "(x) > 0 x (a; b)— график выпуклый вниз.

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x  ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x  ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, чтоесли в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

34.

Необходимое и достаточные условия перегиба. Необходимое условие перегиба.

Сформулируем необходимое условие перегиба графика функции.

Пусть график функции y=f(x) имеет перегиб в точке  и имеет при непрерывную вторую производную, тогда выполняется равенство .

Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения , в которых вторая производная равна нулю, являются абсциссами точек перегиба.

Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все  из области определения функции, для которых  и . Обычно это точки, в которых знаменатель первой производной обращается в ноль.