Г Л А В А 9. Квантово-размерные структуры. Основы нанотехники 287

Г л а в а 9 квантово-размерные структуры. Основы нанотехники

(особенности квантово – размерных структур)

По мере приближения характерного размера твердотельной структуры электронного прибора к нанометровой области, соизмеримой с размерами атомов, проявляются квантовые свойства электронов. Если в микроэлектронных приборах поведение электрона определялось поведением элементарной частицы, имеющей массу и заряд, то в наноэлектронных приборах поведение электрона определяется его волновыми свойствами. Структуры, в которых проявляются волновые свойства электронов, называют квантово-размерными или наноразмерными структурами.

С позиций квантовой механики электрон может быть представлен волной, описываемой соответствующей волновой функцией. Распространение этой волны в квантово-размерных твердотельных структурах контролируется эффектами, связанными с квантовым ограничением, интерференцией и возможностью туннелирования через потенциальные барьеры.

Работа приборов на основе наноразмерных структур во многом основана на туннельном эффекте, заключающемся в прохождении частицы через потенциальный барьер конечной ширины. Коротко рассмотрим механизм этого явления.

9.1. Прохождение микрочастицы через узкий потенциальный барьер

Из наличия у микрочастиц волновых свойств следует, что закон движения их должен определяться законом распространения волн де Бройля, связанных с этими частицами. Так как распространение любого волнового процесса описывается волновым уравнением, то следует ожидать, что и движение микрочастиц должно описываться волновым уравнением. Такое уравнение было найдено впервые Шредингером и носит его имя. В одномерном случае для микрочастицы, например, электрона, движущегося в силовом поле и обладающей потенциальной энергии W_п(x,t) амплитудное уравнение Шредингера имеет следующий вид:

, (9.1)

где (x) – амплитудная волновая функция;W– полная энергия частицы;m- масса частицы;W_п= W_п(x,t).

Волновые функции Ψ должны быть нормированы так, чтобы интеграл от плотности вероятности по всей рассматриваемой точке пространства был равен единице, то есть , где– радиус-вектор точки, Ψ* - комплексно-сопряженная функция. Это возможно, если, гдеV – объем тела, в котором движется электрон.

Рассмотрим прохождение частицы через потенциальный барьер конечной толщины d(туннельный эффект). Процесс туннелирования электронов заключается в квантовом переходе системы через потенциальный барьер в случае, когда энергия электронов меньше высоты потенциального барьера.

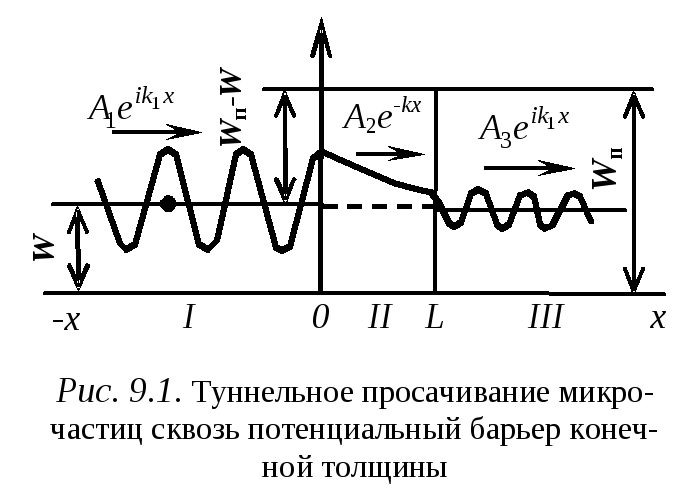
Пусть микрочастица движется вдоль оси xв пространстве, в котором силовое полеW_пменяется скачком, как показано на рис. 9.1. В областиI, простирающейся от -до 0, потенциальная энергияW_п=0, кинетическая энергияW_к=W; в областиII, простирающейся от 0 доL, потенциальная энергия равнаW_п, причемW_к=W – W_п ; в областиIII, простирающейся отLдо +потенциальная энергия опять равна нулю.Таким образом, при переходе из областиIв область II для микрочастицы существует потенциальный барьер высотойW.

Движение микрочастицы описывается уравнением Шредингера (9.1). Напишем его для областей IиII.

Для области I

, (9.2)

где ₁– волновая функция микрочастицы в областиI;

–волновое число микрочастицы в области I(см. формулу (1.22))

Для области II

, (9.3)

где ₂– волновая функция микрочастицы в областиII;

–волновое число микрочастицы в области II.

Для области III

, (9.4)

где ₃– волновая функция микрочастицы в областиIII;

–волновое число микрочастицы в области III.

Общие решения уравнений (9.2), (9.3) и (9.4) имеют следующий вид:

при x<0; (9.5)

при 0<x<L. (9.6)

при x>L; (9.7)

Слагаемое A₁exp(ik₁x) соответствует волне, распространяющейся в областиIв направлении осиx,A₁– амплитуда этой волны. СлагаемоеB₁exp(-ik₁x) соответствует отраженной от барьера волне с амплитудойB₁, распространяющейся в областиIв направлении, противоположномx. Так как вероятность нахождения микрочастицы в том или ином месте пространства пропорциональна квадрату амплитуды волны де Бройля, то отношение

представляет собой коэффициент отражениямикрочастицы от барьера.

Слагаемое A₂exp(ik₂x) соответствует волне, распространяющейся в областиIIв направленииx. Квадрат амплитуды этой волны определяет вероятность проникновения микрочастицы в областьII. Отношение

представляет собой коэффициент прозрачностибарьера.

Слагаемое B₂exp(-ik₂x) должно соответствовать отраженной волне, распространяющейся в областиII. Так как такой волны нет, тоB₂=0.

Для барьера, высота которого W_п>W, волновое число k₂ является мнимым. Положим его равным ik, где является действительным числом. Тогда решение уравнения (9.3) можно написать в виде:

при x>0. (9.8)

Тот факт, что A₂0, означает, что имеется вероятность проникновения микрочастицы на некоторую глубину во вторую область. Эта вероятность пропорциональна квадрату модуля волновой функции₂:

. (9.9)

Из выражения (9.9) следует, что наличие вероятности проникновения микрочастицы на некоторую глубину в область II, делает возможным прохождение (просачивание) микрочастиц сквозь потенциальный барьер конечной толщиныL. Такое просачивание получило названиетуннельного эффекта.

Значение коэффициента прозрачности Dпрямоугольного барьера изображенного на рис. 9.1 можно рассчитать по формуле

, (9.10)

где A₃– амплитуда волны, распространяющейся в областиIIIв направлении осиx.

Слагаемое B₃exp(-ik₁x) должно соответствовать отраженной волне, распространяющейся в областиIII. Так как такой волны нет, тоB₃=0.

Полагая в выражении (9.10) A=A₃, а значениеA₁=1, для коэффициента прозрачности прямоугольного потенциального барьера конечной толщиныLполучаем выражение

, (9.11)

где D₀1 – коэффициент пропорциональности.

Очевидно, что с уменьшением полной энергии микрочастицы величина коэффициента прозрачности Dуменьшается. Практически приd >1,5 нм величинаD0 для любыхW_п – W >0. Таким образом, туннельный эффект заключается в том, что микрочастицы могут проходить через тонкий барьер, когда полная энергия частицыWменьше ее потенциальной энергииU_п, то есть меньше высоты барьера. В таблице 9.1 [2] приведены значенияDдля барьеров разной толщиныL, но одной и той же высотыW_п – W=5 эВ.

Таблица 9.1

L, нм	0,1	0,15	0,2	0,5	1,0
D	0,1	0,03	0,08	1,110-5	1,1510-10

Из данных, приведенных в таблице 9.1, следует, что барьеры между атомами в кристалле (при межатомных расстояниях 0,3…0,5 нм) имеют достаточно высокую прозрачность. Замечательным является то, что при туннельном просачивании сквозь потенциальный барьер энергия микрочастиц не меняется: они покидают барьер с той же энергией, с какой в него входят.

Туннельный эффект играет большую роль в электронных приборах. Он обуславливает протекание таких явлений, как эмиссия электронов из твердого тела под действием сильного электрического поля, прохождение тока через диэлектрические пленки, пробой p-nпереходов; на его основе созданы туннельные диоды, разрабатываются активные пленочные элемент и пр. Туннельный эффект лежит в основе действия туннельного микроскопа