1.4.11. Коэффициент теплопроводности, коэффициент динамической вязкости газовой смеси.

1.4.11.1. Бинарные смеси

• В работе , для бинарных газовых смесей (смесей двух газов) рекомендован универсальный метод расчета коэффициентов теплопроводности и динамической вязкости.

- Коэффициент теплопроводности смеси:λ _см , Вт / (м · К):

,

где: и- коэффициенты теплопроводности первого и второго

компонентов бинарной смеси, взятые при температуре смеси.

- поправочные коэффициенты.

Здесь: - коэффициенты динамической вязкости компонентов

- молекулярные массы компонентов.

1. Коэффициент динамической вязкости смесиη_см, Па · С:

Средняя погрешность вычисления по этому методу составляет примерно 4%, а погрешность вычисления- в среднем 2%.

• Бинарные смеси являются наиболее исследованными. Опыт показывает следующее :

1. При малыхразличиях в значениях молекулярной массы компонентов величина коэффициента теплопроводности смеси подчиняется условиюаддитивности:

2. При большомразличии молекулярных масс компонентов (смеси водорода) лучшее согласование с опытом даетлогарифмическаязависимость

или

3. Во всех остальных случаях истинное значение находится в области, ограниченной вышеприведенными значениями, т. е.

1.4.11.2. Многокомпонентные смеси

• Коэффициент динамической вязкости многокомпонентной смеси можно определить с использованием методов Гиршфельдера и его школы [3].

Эти методы дают хорошее согласование с опытом, особенно для коэффициента вязкости, но используют громоздкие и неудобные для практики формулы. В связи с этим получили распространение более простые аппроксимационные формулы, например, приближенная формула Уилке [4]:

,

где: - мольная (объемная) концентрацияi-го компонента смеси.

Погрешность результатов расчетов по формуле Уилке по сравнению с опытом находится в пределах 4%.

Коэффициент теплопроводности -компонентной газовой смеси можно определить по приближенной формуле Масона-Саксена [4]:

• В работе [5] для газовых смесей рекомендуется формула Брокау:

где: и

2. Смешение газов

Пусть смешиваютсяn химически невзаимодействующихмежду собойидеальныхгазов. Предполагается, что известны начальные термодинамические параметры состояния всех компонентов до смешения и условия смешения (условия взаимодействия с окружающей средой). Требуется найтиравновесные параметры состояния газов после смешения.

Рассмотрим два случая смешения, для простоты полагая, что этот процесс идет без теплообмена с окружающей средой.

2.1. Смешение при W=Const

В этом случае условия смешения таковы, что объем образующейся смеси W_см равен сумме начальных объемов компонентов смесиW_{H i}:

.

(Не следует путать W_{H i}с парциальными объемамиW_i, рассмотренными в параграфе 1.4.3.)

Обозначим:

Р_{H i} – начальное давлениеi-го газа;

Т_{H i} , t_{H i} – начальная температураi-го газа соответственно в⁰Кили⁰С.

Т.к. вся система из nгазов при смешении в условияхW=Const не совершает внешней работы, то в соответствии с первым началом термодинамики для этого случая () можно записать:

(2.1.1)

Здесь: U_см– внутренняя энергия смеси газов массойm_см килограммов

с температурой Т⁰ К;

U_{H i}- внутренняя энергияi-го газа массойm_i килограммов

с начальной температурой Т_{H i}.

Введем обозначения:

u_см – удельная внутренняя энергия смеси газов при температуреТ⁰ К;

u_{H i} – удельная внутренняя энергияi-го газа с начальной температуройТ_{H i.}

Тогда уравнение (2.1.1) принимает следующий вид:

(2.1.2)

Как известно, для идеального газа du=C_v dT, откуда при отсчете внутренней энергии от0⁰ К можно записать:

и . (2.1.3)

Здесь: - средняя в диапазоне0Т⁰ К массовая изохорная теплоемкость смеси газов;

- средняя в диапазоне0Т_{H i} ⁰К массовая изохорная теплоемкостьi-го газа.

После подстановки (2.1.3) в (2.1.2) получим:

. (2.1.4)

Но в соответствии с параграфом 1.4.10 истинная массовая теплоемкость смеси газов выражается через массовые доли компонентов g_iи их истинные теплоемкости следующим образом:

.

Аналогично средняя в диапазоне 0Т⁰ К массовая изохорная теплоемкость смеси газов определится как:

.

Подставляя это выражение в левую часть уравнения (2.1.4) получим:

,

откуда (2.1.5)

Т.к. из уравнения состояния , то после подстановкиm_iв уравнение (2.1.5) окончательно получим формулу для температуры смесиnгазов:

(2.1.6)

Как известно, , поэтому формула (2.1.6) может быть записана в следующем виде:

(2.1.7)

(Следует напомнить, что произведение - это средняя в диапазоне 0- Т_{H i} ⁰К молярная изохорная теплоемкостьi-го газа.)

В справочной литературе эмпирические зависимости теплоемкости от температуры часто даются для диапазона 0t ⁰ С.

Тогда:

и , (2.1.8)

где (2.1.9)

После подстановки (2.1.8) и (2.1.9) в уравнение (2.1.2) получим:

,

откуда .

Заменяя m_iего значением, окончательно получим формулу для температуры смеси газов в градусахЦельсия:

(2.1.10)

Выражая R_iчерез малекулярную массу, получим еще одну формулу:

(2.1.11)

В знаменателях формул (2.1.6), (2.1.7), (2.1.10) и (2.1.11) содержатся средние теплоемкости, у которых в качестве верхнего предела осреднения используется температура смеси (tилиТ), подлежащая определению. В силу этого, температура смеси по этим формулам определяетсяметодом последовательных приближений.

2.1.1. Частные случаи смешения газов при W=Const

Рассмотрим несколько частных случаев формул (2.1.6), (2.1.7), (2.1.10) и (2.1.11).

1. Пусть смешиваются газы, у которых зависимостью показателя адиабаты К_iот температуры можно пренебречь.

(В действительности К убывает с ростом температуры, т. к.

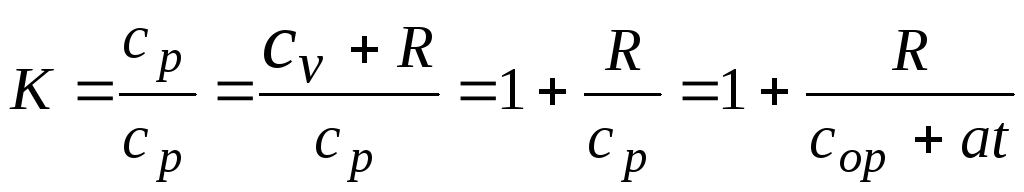
гдес_{о р ,} а–эмперические положительные коэффициенты.

Для технических расчетов в диапазоне от 0 до 2000⁰С можно пользоваться следующими формулами:

а) для двухатомных газовК 1,40- 0,5010^-4 t;

б) для продуктов сгоранияК 1,35- 0,5510^-4 t.

Из этих формул видно, что влияние температуры на показатель адиабаты К становится заметным лишь при температурах, порядка сотен градусов по шкале Цельсия.)

Т. о., если допустить, что

,

то формула (2.1.6) примет следующий вид:

(2.1.12)

Формулу (2.1.12) можно использовать в качестве первого приближения для формул (2.1.6), (2.1.7), (2.1.10) и (2.1.11)

2. Пусть смешиваются газы, у которых мольные изохорные теплоемкости равны и зависимостью этих теплоемкостей от температуры можно пренебречь, т. е.:

.

Тогда уравнение (2.1.7) принимает очень простой вид:

(2.1.13)

Если у газов равны между собой мольные изохорные теплоемкости, то в соответствии с уравнением Майера

,

должны быть равны между собой и мольные изобарные теплоемкости, а, следовательно, равны и показатели адиабаты, т. е.

.

При этом условии уравнение (2.1.12) превращается в (2.1.13).

2.1.2. Давление после смешения газов при W=Const

Давление, устанавливающееся после смешения газов, можно определить либо по формулам параграфа 1.4.2, либо из условия:

Р_смW_см =m_смR_смТ =m_смТ .

Откуда

или

(2.1.14)

Для частного случая 2 давление смеси получим путем подстановки формулы (2.1.13) в (2.1.14), откуда