1.4.3.Парциальный объем.

Для сравнения количества газов в смеси по объему, необходимо их объемы при температуре смеси привести к одинаковому давлению.

Если этим одинаковым давлением является давление смеси , то приведенные к этому давлению объемы компонентов называются парциальными.

Парциальный (приведенный) объем - это объем, который занимал бы i-тый компонент, если бы он один находился при температуре и давлении смеси .

Для понимания физического смысла парциального объема рассмотрим смесь двух идеальных газов. Как отмечалось ранее, молекулы обоих газов равномерно распределены по всему объему , занимаемому смесью при давлении и температуре .

Представим себе, что каким-то образом удалось разделить молекулы этих двух газов так, что в общем объеме первый газ занимает объем , а второй - при одинаковой температуре . Для того, чтобы эта гипотетическая система находилась в равновесии и газы не смешивались за счет разности давлений, давление в объемах и должно быть одинаковым и равным общему давлению смеси , т. е.

Или в общем случае

Типичной студенческой ошибкой является подстановка в это уравнение вместо давления смеси величины парциального давления .

1.4.4. Задание состава смеси идеальных газов объемными долями.

Во многих практических задачах состав смеси газов задается объемными долями:

,

где: - парциальный объем i-го газа в составе смеси газов, занимающей объем .

Установим связь между объемными и мольными долями газов смеси.

Т. к. универсальная газовая постоянная Дж / (кмоль · К)

связана с удельными газовыми постоянными , Дж / (кг · К), соотношением

,

то из определения парциального объема идеального газа в составе смеси получим:

или ,

где: -число киломолей i-го газа.

Просуммировав значения для всех газов, входящих в смесь, получим

,

где: и

Разделив выражения для на выражение для получим

Т. о. для смеси идеальных газов мольная и объемная доли i-го газа равны между собой по величине

.

и

.

1.4.5. Формулы пересчета для различных способов задания состава газовых смесей

Получим формулу пересчета мольных долей на массовые и наоборот.

Т. к. и , то .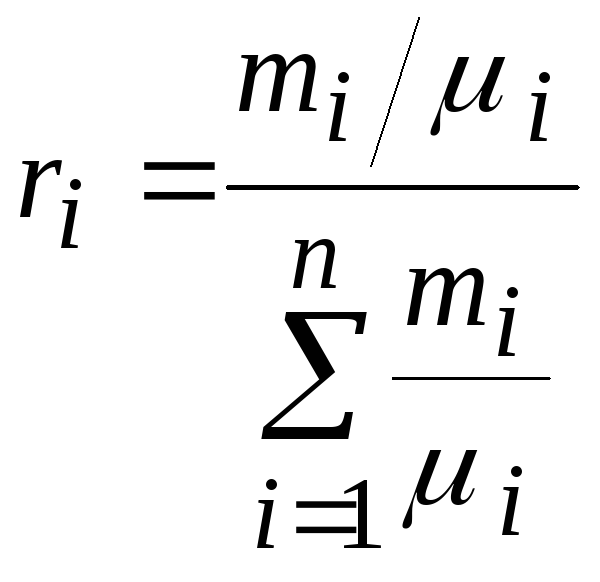

Разделив числитель и знаменатель полученного выражения на массу смеси получим

,

или окончательно:

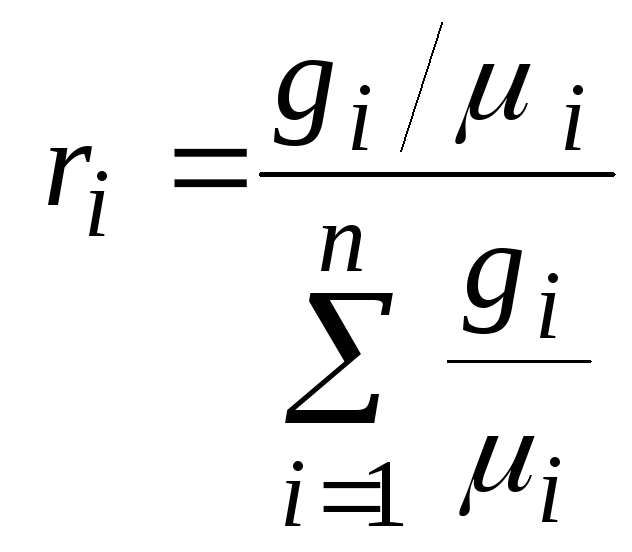
Т. к. и ,

то .

Разделив числитель и знаменатель этого выражения на получим ,

или окончательно

1.4.6. Кажущаяся молекулярная масса смеси газов

Для упрощения расчетов смесь идеальных газов условно полагают однородным газом с той же суммарной массой и с тем же суммарным числом молекул, равным

,

где - число молекул в единице объема смеси газов;

- число Авогадро (число молекул в одном киломоле вещества):

, 1 / кмоль

Молекулярная масса такого однородного газа обозначается и называется кажущейся молекулярной массой смеси:

.

Разделив числитель и знаменатель этого выражения на , получим ,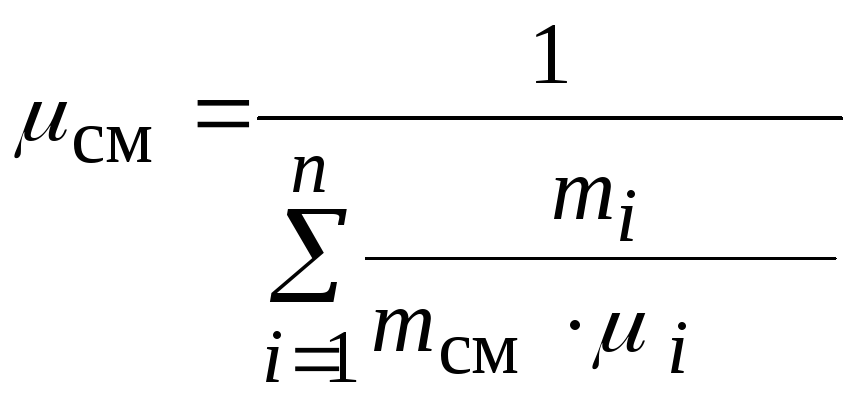

или окончательно

Через мольные доли величина выражается проще:

,

или окончательно