
МетодГаусса
.pdfТЕОРЕМА ОБ LU-РАЗЛОЖЕНИИ
Пусть все угловые миноры матрицы А отличны от нуля, j ≠0, j=1,2 ,... , m. Тогда матрицу А можно представить, причем единственым образом, в виде
произведения |
A=LU , |
(1) |
|
где L – нижняя треугольная матрица с ненулевыми диагональными элементами, U – верхняя треугольная матрица, на диагонали которой стоят единицы.
1 =a11 , 2 |
=det a21 a22 ,... , |
m =det A |
(2) |
|
a11 a12 |
|
|
l11 |
0 |
|
0 |
|
|
1 |
u12 |
u1m |
|
|||
L= |
|
l12 |
l22 |
|
0 |
|
(3) |
U = |
0 |
1 |
u2m |
(4) |
|
|
|
|
|
|
|
|
|
|
|||||
|
lm1 l m2 lmm |
|
0 |
0 |
|
1 |
|
||||||
МЕТОД ГАУССА
Пусть дано уравнение: |
A x= ̄f |
|
|
|
(5) |
|
|
|
|
|
|
||
|
̄ |
|
|
|
|
|
|
LU x=̄f |
|
|
|
(6) |
|
|
̄ |
|
|
|
|
|
Решение системы уравнений (6): |
|
|
|
|
|
|
̄ ̄ |
(7) |
y |
−1 |
̄ (9) |
||
|
=L |
|
f |
|
||
U x=y |
|
̄ |
|
|
|
|
L y=̄f (8) |
|
|
|
|
||
x=U |
−1 |
y |
(10) |
|||
̄ |
|
|
|
|||
|
|
̄ |
|
|
̄ |
|
Покомпонентный вид:
{a11 x1+a12 x2+ +a1m xm= f a21 x1+a22 x2+ +a2m xm= f
am1 x1+am2 x2+ +amm xm= f
1 |
|
x1+u12 x2+ +u1m xm= y1 |
|
0 +x2+ +u2m xm= y2 (12) |
|
2 |
|
|
m |
(11) |
{0+0+ +xm=ym |
m
xk= yk− ∑ ukj x j , k =m ,1 (13)
j=k+1
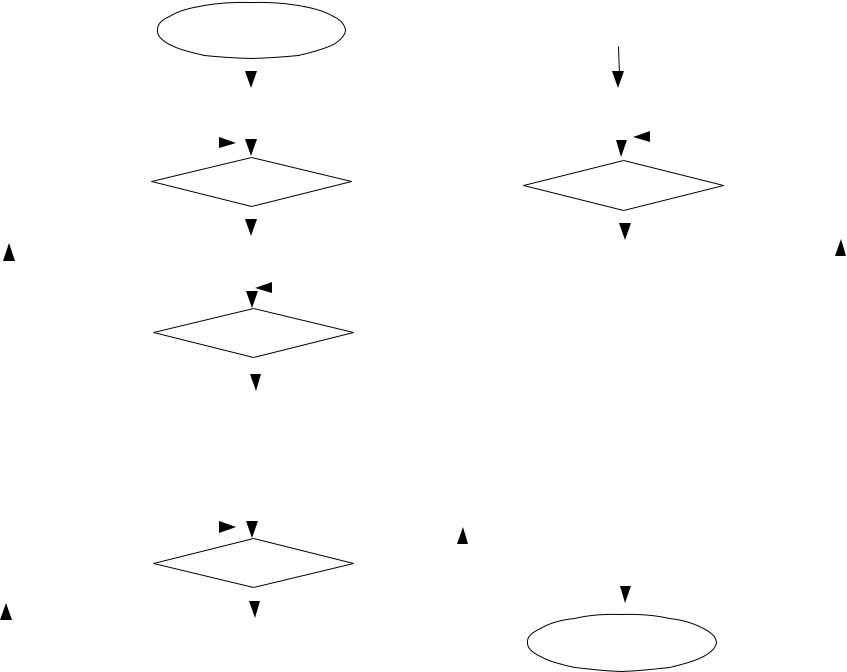
АЛГОРИТМ МЕТОДА ГАУССА
|
|
|
|
|
|
Начало |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k :=1 |
|
|
|
|
|
|
|
|
|
|
k :=m |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
k ≤m−1 |
|
|
|
|
|
|
|
k ≥1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k :=k −1 |
|
k :=k +1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i :=k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f k − ∑ akj x j |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
|
|
|
i≤m |
|
|
|
|
|
|
xk := |
|
|
|
|
j =k +1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
akk |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tik =aik /akk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
f i= f i−tik ak |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
j :=k +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
i :=i+1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
j≤m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
j := j+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
aij=aij−tik akj |
|
|
|
|
|
|
|
|
|
|
Конец |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Рисунок 4 – Алгоритм метода Гаусса
