geodezia_v_voprosakh_i_otvetakh

Пример7. Один и тот же угол измерен теодолитом 2Т30П (β1=35º 15,5′) и Т5 ( β2 =35º 15,1′). Вычислить среднее значение угла.

Так как приборы имеют различную точность, то необходимо сначала установить веса результатов измерений. Очевидно, что Рβ1=µ/mβ12, а Рβ2=µ/mβ2 2. Примем µ = 100, тогда Рβ1 = 0,11 и Рβ2 = 4. В соответствии с (3.22) получим

β0= 35º 15,0′ + ((0,5*0,11+0,1*4)/4,11)= 35º 15,1′.

Как видим из примера, измерение угла теодолитом 2Т30П ни как не оказало влияние на среднее значение угла, то есть было бесполезным. В тоже время, если не учитывать веса измеренных углов, то среднее значение угла будет равно β = 35º 15,3′. Различие существенное.

В качестве константы µ целесообразнее принимать не обезличенное число, а квадрат средней квадратической погрешности одного из результатов измерений. В рассматриваемом примере в качестве µ можно принять mβ1 или mβ2. В этом случае µ есть средняя квадратическая погрешность единицы веса.

3.18. Как оценить точность арифметической средины из неравноточных измерений?

Очевидно, что как и при обработке ряда равноточных измерений, точность арифметической средины выше, чем точность любого отдельно

квадрата средней квадратической погрешности, т.е. µ = mβ12. Тогда Рβ1= 1, а Рβ2 = 36. В этом случае [p] = 37. Подставив в (3.23), имеем Mβ0 = 4,9″. Такой же результат получим и при других значениях µ. Например, в качестве µ примем mβ2 = 5″. Получим Mβ0 = 5″/√1,0277 = 4,9″.

3.19. Какие другие качественные параметры измерений можно принимать в качестве весов (кроме средних квадратических погрешностей)?

В качестве весов измерений можно принимать и другие качественные характеристики, значения которых пропорциональны величинам средних квадратических погрешностей. К ним относятся: число приемов измерений; невязки геометрических фигур; длины нивелирных и теодолитных ходов и т.д.

41

Очень часто приходится обрабатывать ряды измерений, компоненты которых являются средними арифметическими, но полученными при разном числе измерений. Покажем, что в этих случаях за вес можно принимать число измерений, на основе которых получена арифметическая средина.

Если в значение веса pi = µ/mi2 вместо средней квадратической погрешности i – го измерения подставить среднюю квадратическую

Пример 8. На учебной практике одну и ту же линию измеряли 4 бригады. Причем первая бригада измерила линию 4 раза, вторая – 10 раз, третья – 6 раз, четвертая – 2 раза. Каждая бригада вычислила среднее арифметическое из своих результатов. Найти общую арифметическую средину из всех измерений?

Таблица3.3.Результаты измерений и вычислений

При наличии ЭВМ или калькулятора вычисление общей арифметической средины необходимо вести по формуле (3.21). а еѐ оценку точности по формуле (3.23). Однако в отдельных случаях более экономичным и оправданным является схема вычисления, изложенная в табл.3.3. Здесь lприб.- приближенное значение искомой величины. Обычно в качестве таковой принимают наименьшее значение из измеренных. Далее находят уклонения результатов измерений от приближенного значения, т.е. δί=li - lприб, а затем вычисляют поправку к приближенному значению как Δ=∑δί pί /∑p. Прибавив поправку к приближенному значению, получаем искомую арифметическую средину L0 .

Оценку точности, так же как и при обработке равноточного ряда, выполняют по формуле Бесселя, применительно к неравноточным измерениям

где µ – средняя квадратическая погрешность измерения одним приемом; v – уклонения от арифметической средины.

По формуле (3.23) вычисляют среднюю квадратическую погрешность общей арифметической средины.

42

Так же как и при обработке равноточных измерений, предельную погрешность принимают равной утроенному значению средней квадратической погрешности. В рассматриваемом примере,

Ml0 =2,3мм, а 3Ml0 =7мм.

3.20. В геодезии часто выполняют измерения и вычисления разнородных величин. Что в этих случаях считается равноточными измерениями?

Действительно, в геодезии часто значение функции находится из результатов угловых и линейных измерений. Поэтому проблема равноточности таких измерений является существенной. Если точность угловых измерений ниже точности линейных, или наоборот, то в результате точность одних может совершенно не оказывать влияния на конечный результат. При уравнительных вычислениях, выполняемых на основе решения линейных уравнений высокого порядка, такая ситуация ведет к потере точности их решения из – за снижения обусловленности матриц. Поэтому проблема установления весов разнородных измерений является актуальной и всегда желательно, чтобы ps = pβ.

Ниже на примерах покажем некоторые приемы предвычисления точности угловых и линейных измерений в простейших геометрических построениях.

Пример 9. Для определения превышения между точками A и B местности были измерены длина линии DAB и угол наклона линии ν (рис.3.3).

Пусть DAB =100м, а угол наклона νAB = 10º. Поставим условие, что угол наклона измерен теодолитом 2Т30П, т.е со средней квадратической ошибкой mν= 30". С какой точностью необходимо измерить длину линии, чтобы влияние угловых и линейных измерений на точность превышения было одинаковое?

Для решения этого вопроса, в соответствии с принципом оценки

43

Совершенно очевидно, что погрешности угловых и линейных измерений окажут одинаковое влияние на точность определения превышения, если в формуле (3.27) поставить условие равенства

Откуда mD = ( D/ tgν) m ν /ρ. Подставив сюда исходные данные, получим md =8,2мм, или в относительной мере md/D=1:12000. Средняя квадратическая погрешность измеренного превышения, при таких параметрах, составит mh =20мм. В этом случае каждое из слагаемых формулы (3.27) вносит в погрешность определения превышения 14мм.

3.21. Известно, что положение точки на плоскости определяется двумя координатами (x,y). Как в этом случае выполнить оценку точности?

Решение поставленного вопроса рассмотрим на примере разбивки осей сооружения способом полярных координат.

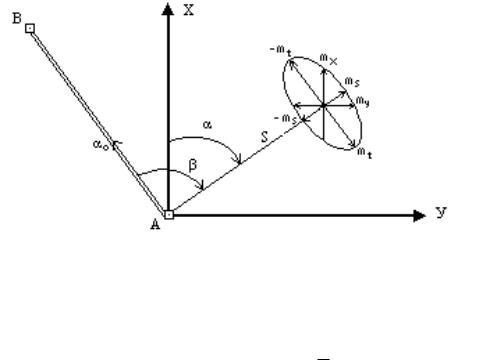
Пример.10. Пересечение осей сооружения (точка О) строится на местности способом полярных координат, т.е. построением проектного угла β от стороны АВ и проектного расстояния S (рис.3.4) от полигонометрического знака А разбивочной геодезической сети. Пусть при

этом S = 20,000 м; 90 00,0 , o 330 00,0 , mS : S 1/ 5000 , m 0,5 . Найти

проекции погрешностей данного построения на оси прямоугольных координат.

Вычислим дирекционный угол стороны АО: α = αо + β = 60о00,0'.

Рис.3.4. Схема построения на местности проектной точки

Средняя квадратическая погрешность откладывания расстояния ( mS ) носит название продольной погрешности, а откладывания угла в линейной

мере называется поперечной погрешностью mt S m .

44

В силу двухмерности положения точки на плоскости область ее определения представляет эллипс рассеивания с длинами полуосей mS и

mt . В частном случае, когда mS = mt (условие равноточности угловых и

линейных измерений), эллипс вырождается в окружность. Это наиболее благоприятный случай, хотя иногда по условиям проекта важно, чтобы продольная погрешность была значительно меньше поперечной mS « mt или

наоборот mS » mt .

Зная mS и mt несложно вычислить погрешности по любому другому

направлению и, в частности, по осям прямоугольных координат. Запишем функции перехода от полярных к прямоугольным координатам в виде

где ρ – число секунд или минут в радиане в зависимости от размерности m . Длина линии должна быть выражена в той же размерности, что и mS .

Подставляя исходные данные в формулы (3.31) и (3.32), будем иметь:

Задача решена, но в практике оценки точности положения точки на плоскости часто вычисляют, кроме названных погрешностей, еще так называемую среднюю квадратическую погрешность положения

Формула (3.33) находит широкое применение не только для анализа точности положения определяемой на местности точки в результате откладывания проектных расстояний и углов, но и для предвычисления точности откладывания расстояния и полярного угла, когда точность положения точки задана проектом (обратная задача). В этом случае чаще

45

всего применяют так называемый принцип равных влияний погрешностей измерения расстояния и полярного угла, то есть приравнивают слагаемые в (3.33)

Подставляя (3.34) в (3.33), получим

В приведенном примере показан подход использования оценки точности функции для расчета погрешностей положения осей здания при разбивке их полярным способом и одновременно подход к предрасчету точности откладывания полярных расстояний и углов, когда точность положения пересечения осей здания задана нормативным документом.

3.22. Что такое невязка?

В геодезической практике кроме необходимых измерений всегда выполняют и избыточные измерения, связанные математическими соотношениями с необходимыми. Например, для решения треугольника, достаточно измерить два угла и сторону. Однако, как правило, измеряют все три угла. Следовательно, одно измерение является избыточным.

Избыточные измерения позволяют надежно контролировать выполненные измерения, осуществлять оценку точности и повышать точность определяемых величин. Контроль измерений осуществляется вычислением невязки и сравнением ее с допустимой. Если вычисленная невязка меньше допустимой невязки, то измерения не содержат грубых погрешностей, в противном случае результаты измерений бракуют.

Сущность невязки покажем на примере треугольника. Пусть в треугольнике измерены все три угла α, β и γ. Истинные значения углов обозначим через α0, β0 и γ0. Следовательно, измеренные углы содержат истинные погрешности Δα, Δβ и Δγ, т.е. α = α0 + Δα, β = β0 + Δβ, γ = γ0 + Δγ.

Если в известное математическое соотношение углов треугольника α0 + β0 + γ0 = 180° подставить вместо истинных значений углов их измеренные

Величина fβ носит название невязки. Таким образом, невязка – это отклонение суммы измеренных величин от теоретической. В общем случае она равна

46

Теоретическая сумма внутренних углов в замкнутом полигоне равна 180о(n-2), превышений и приращений координат равна нулю. В разомкнутых ходах, опирающихся на твердые пункты, теоретическая сумма вычисляется как:

где индексы К и Н означают «конечный» и «начальный». С учетом изложенного, невязки вычисляют:

а) угловую в замкнутом теодолитном полигоне

д) приращений координат в разомкнутом полигоне

е) превышений в разомкнутом нивелирном ходе

Невязка есть сумма накопленных случайных погрешностей измерений. Она зависит от условий измерений и характеризует качество выполненных измерений. С этой целью в нормативных документах на производство работ устанавливают требования к точности измерений и на их основе допустимую невязку. Еѐ обозначают fдоп. и с ней сравнивают полученные невязки. Если они меньше допустимых, то измерения выполнены качественно, в противном случае измерения бракуют.

47

3.23. В чем смысл уравнительных вычислений?

В силу наличия избыточных измерений и образующихся при этом невязок, при вычислении функции от измеренных величин возникает неоднозначность. Для ликвидации неоднозначности выполняют уравнивание, которое заключается в отыскании вероятнейших поправок к измеренным величинам. Обязательным условием при этом является равенство сумм исправленных величин теоретическим. Следовательно, невязки после введения поправок должны быть равны нулю. С математической точки зрения процесс отыскания поправок V к измеренным величинам сводится к отысканию min функции [PV2].

равноточные. Выполнить уравнивание.

Порядок решения данной задачи следующий:

1. Вычисляем сумму измеренных углов и находим невязку

fβ = 180 00,0 0,6 ,

2.Вычисляем допустимую невязку fβ доп и сравниваем с ней полученную

доп. f 13 1,8 ; fβ< fβ доп .

3.Так как углы измерены равноточно, то полученную невязку распределяем поровну в виде поправок к измеренным углам. При этом поправки всегда имеют знак, противоположный невязке. То есть

V 0,6 0,2 . 3

4.Вычисляем исправленные углы

63 18,5 0,2 63 18,7 ,

56 12,6 0,2 56 12,8 ,

60 28,3 0,2 60 28,5 .

5.Вычисляем сумму исправленных углов

63 18,7 56 12,8 60 28,5 180 00,0 .

Уравнивание выполнено.

Предлагается экспериментально проверить, что полученные поправки удовлетворяют условию V 2 min .

Пример 12. В треугольнике измерены три угла теодолитами различной точности. Угол 1 измерен теодолитом Т30 и равен 63º18'30", угол 2 теодолитом Т5 и равен 56º12'36" и угол 3 измерен теодолитом Т1 и равен

60º28'20". Выполнить уравнивание. Порядок решения.

48

1. Вычисляем сумму измеренных углов и находим невязку

f 63 18 30 56 12 36 60 28 20 180 00 00 34 .

Так как измерения не равноточные, то и на формирование невязки они

2.Вычисляем веса результатов измерений в соответствии с (3.20), приняв μ = 100.

3. Находим поправки к измеренным величинам как

где qi = 1 / pi .

Численные значения поправок равны

То есть поправки вполне удовлетворяют логику, что основная часть невязки содержит погрешность от измерения угла теодолитом Т30.

Предлагается экспериментально проверить, что полученные поправки удовлетворяют условию [pi v2i ] = min.

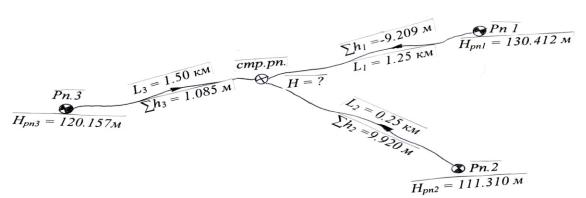
Пример 13. Для передачи отметки на строительный репер строительной площадки проложено три нивелирных хода от реперов с имеющимися отметками (рис.3.5). Вычислить вероятнейшее значение отметки строительного репера.

Рис.3.5. Схема передачи высоты на строительный репер

Здесь причина не равноточности измерения состоит в том, что длины ходов, по которым передавалась отметка на строительный репер, различны. При вычислении отметки строительного репера получили три значения, отличающиеся друг от друга. Это является результатом накопления погрешностей измерений (табл. 3.4). Необходимо вычислить вероятнейшее значение высоты строительного репера, т.е. выполнить уравнивание.

49