2. Использование полиморфизма в ооп.

Полиморфи́зм — возможность объектов с одинаковой спецификацией иметь различную реализацию.

Язык программирования поддерживает полиморфизм, если классы с одинаковой спецификацией могут иметь различную реализацию — например, реализация класса может быть изменена в процессе наследования. Кратко смысл полиморфизма можно выразить фразой: «Один интерфейс, множество реализаций».

Полиморфизм позволяет писать более абстрактные программы и повысить коэффициент повторного использования кода.

Примером полиморфизма является различная реализация методов отображения геометрических фигур на экране, различная реализация методов чтения\записи в классах-потоках, и др.

Виды полиморфизма.

1. Полиморфизм переопределения. При наследовании дочерний объект переопределяет метод или атрибут родителя.

2. Параметрический полиморфизм. В C++ перегрузка имён функций, шаблоны функций. Разные функции с одинаковыми идентификаторами могут принимать разные наборы аргументов различных типов. Назначение перегрузки, шаблонов: разрешить выполнять одну и ту же операцию с разными операндами, используя единственное имя функции.

// Перегрузка int max(int num_1,int num 2); double max(double num_1, double num 2); int max (double num_1, double num 2); { If (num_1>num_2) Return num_1; Else Return num_2; } double max (double num_1, double num 2);

{ If (num_1>num_2) Return num_1; Else Return num_2; } // Шаблон template<typename T> T max(T num_1, T num 2); { If (num_1>num_2) Return num_1; Else Return num_2; }

2. Математическая логика и теория алгоритмов.

2.1. Логические операции. Таблицы истинности.

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно (На улице идёт дождь – высказывание, какая хорошая погода – не высказывание).

Высказывания А и В равносильны тогда и только тогда, когда истинностные значения А и В совпадают ().

Таблица истинности – таблица, описывающая логическую операцию (или функцию), в ней перечислены все значения логической операции для всех возможных значений аргументов.

Логические операции над высказываниями.

1. Отрицание. . Не а. Унарная операция.

   a
   0	1
   1	0

2. Конъюнкция. . a И b.

   a	b
   1	1	1
   1	0	0
   0	1	0
   0	0	0

3. Дизъюнкция. . a ИЛИ b.

   a	b
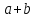
   1	1	1
   1	0	1
   0	1	1
   0	0	0

4. Импликация. 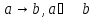. ЕСЛИ a, ТО b. a – посылка, b – заключение.

   a	b
   1	1	1
   1	0	0
   0	1	1
   0	0	1

5. Эквиваленция. 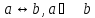. ТОГДА И ТОЛЬКО ТОГДА

a	b
1	1	1
1	0	0
0	1	0
0	0	1

Если х делится на 4, то x делится на 2.

А: х делится на 4.

B: х делится на 2.

Формулы.

1. Снятие импликации

2. Снятие эквиваленции

3. Переместительный (коммуникативный) закон ,

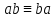4. Сочетательный (ассоциативный) закон ,

5. Распределительный (дистрибутивный) закон ,.

6. Законы Де Моргана ,

7. Законы поглощения ,.

8. Законы идемпотентности ,.

9. Законы нуля и единицы ,,,

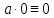10. Закон исключающего третьего

11. Закон противоречия

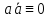
12. Закон двойного отрицания