ТВиМС

Задача 21. Дана плотность распределения  случайной величины . Найти параметр , математическое ожидание , дисперсию , функцию распределения случайной величины , вероятность выполнения неравенства .

Варианты 1–8: 

Варианты 9–16: 

Варианты 17–24: 

Варианты 25–31: 

21.1.	21.2.
21.3.	21.4.
21.5.	21.6.
21.7.	21.8.
21.9.	21.10.
21.11.	21.12.
21.13.	21.14.
21.15.	21.16.
21.17.	21.18.
21.19.	21.20.
21.21.	21.22.
21.23.	21.24.
21.25.	21.26.
21.27.	21.28.
21.29.	21.30.
21.31.

Задача 30. Двумерная случайная величина  имеет равномерное распределение вероятностей в треугольной области , т.е.

где S – площадь . Определить маргинальные плотности распределения  и  случайных величин  и , математические ожидания , дисперсии , коэффициент корреляции r. Являются ли случайные величины  и  независимыми?

30.1.
30.2.
30.3.
30.4.
30.5.
30.6.
30.7.
30.8.
30.9.
30.10.
30.11.
30.12.
30.13.
30.14.
30.15.
30.16.
30.17.
30.18.
30.19.
30.20.
30.21.
30.22.
30.23.
30.24.
30.25.
30.26.
30.27.
30.28.
30.29.
30.30.
30.31.

Задача 34. Известно, что случайная величина  имеет распределение Пуассона 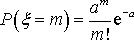, неизвестным является параметр a. Используя указанный ниже метод получения точечных оценок, найти по реализации выборки  значение оценки  неизвестного параметра a.

Варианты 1–15. Метод моментов.

Варианты 16–31. Метод максимального правдоподобия.

34.1.
34.2.
34.3.
34.4.
34.5.
34.6.
34.7.
34.8.
34.9.
34.10.
34.11.
34.12.
34.13.
34.14.
34.15.
34.16.
34.17.
34.18.
34.19.
34.20.
34.21.
34.22.
34.23.
34.24.
34.25.
34.26.
34.27.
34.28.
34.29.
34.30.
34.31.

Задача 35. Известно, что случайная величина  имеет биномиальное распределение , неизвестным является параметр р. Используя указанный ниже метод получения точечных оценок, найти по реализации выборки  значение оценки  неизвестного параметра р.

Варианты 1–15. Метод максимального правдоподобия.

Варианты 16–31. Метод моментов.

35.1.
35.2.
35.3.
35.4.
35.5.
35.6.
35.7.
35.8.
35.9.
35.10.
35.11.
35.12.
35.13.
35.14.
35.15.
35.16.
35.17.
35.18.
35.19.
35.20.
35.21.
35.22.
35.23.
35.24.
35.25.
35.26.
35.27.
35.28.
35.29.
35.30.
35.31.

Задача 36. Случайная величина  имеет нормальное распределение с неизвестным математическим ожиданием а и известной дисперсией . По выборке  объема n вычислено выборочное среднее . Определить доверительный интервал для неизвестного параметра распределения a, отвечающий заданной доверительной вероятности .

 

36.1.
36.2.
36.3.
36.4.
36.5.
36.6.
36.7.
36.8.
36.9.
36.10.
36.11.
36.12.
36.13.
36.14.
36.15.
36.16.
36.17.
36.18.
36.19.
36.20.
36.21.
36.22.
36.23.
36.24.
36.25.
36.26.
36.27.
36.28.
36.29.
36.30.
36.31.

Задача 37. Случайная величина  имеет нормальное распределение с неизвестными математическим ожиданием а и дисперсией . По выборке объема n вычислены оценки

 и 

неизвестных параметров. Найти доверительный интервал для математического ожидания а, отвечающий доверительной вероятности .

37.1.
37.2.
37.3.
37.4.
37.5.
37.6.
37.7.
37.8.
37.9.
37.10.
37.11.
37.12.
37.13.
37.14.
37.15.
37.16.
37.17.
37.18.
37.19.
37.20.
37.21.
37.22.
37.23.
37.24.
37.25.
37.26.
37.27.
37.28.
37.29.
37.30.
37.31.

Задача 38. В результате n опытов получена несмещенная оценка  для дисперсии нормальной случайной величины. Найти доверительный интервал для дисперсии при доверительной вероятности .

 

38.1.	38.2.
38.3.	38.4.
38.5.	38.6.
38.7.	38.8.
38.9.	38.10.
38.11.	38.12.
38.13.	38.14.
38.15.	38.16.
38.17.	38.18.
38.19.	38.20.
38.21.	38.22.
38.23.	38.24.
38.25.	38.26.
38.27.	38.28.
38.29.	38.30.
38.31.