Глава 14. Степенные ряды.

14.1 Функциональные ряды.

Ряд называется функциональным, если его члены являются функциями от:.(1). Даваяопределенные числовые значения, получим различные числовые ряды, которые могут сходится и расходится.

Совокупность тех значений , при которых функциональный ряд сходится, называетсяобластью сходимости ряда.

В области сходимости ряда его сумма является функцией х:.

Пример. . Этот ряд сходится при(убывающая геометрическая прогрессия). Очевидно,=при.

Пусть – сумма первыхnчленов ряда (1). Если этот ряд сходится и его сумма равна, то=+, где=– остаток ряда.

Для всех хв области сходимости ряда, поэтому.

14.2. Степенные ряды.

Степенным рядом называется функциональный ряд вида (1), где– числа – коэффициенты ряда.

Теорема Абеля.

1. Если степенной ряд сходится при некотором значении , то он абсолютно сходится при всяком значении, для которого.

2. Если ряд расходится при некотором значении , то он расходится при всяком, для которого.

Доказательство.

1. Т.к. числовой ряд сходится, то его общий членпри. Это значит, что существует такое число, что все члены ряда по модулю. Перепишем ряд (1) в виде:и запишем ряд из модулей:. Члены этого ряда меньше соответствующих членов ряда: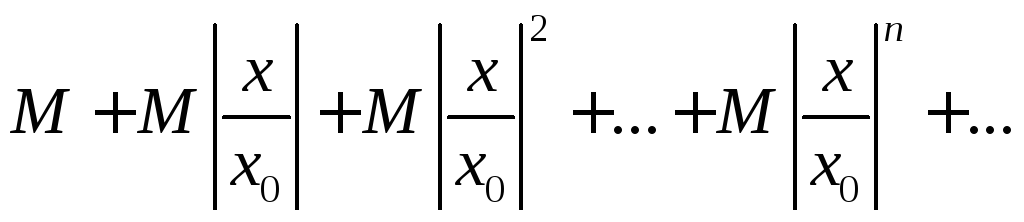. Припоследний ряд – геометрическая прогрессия со знаменателем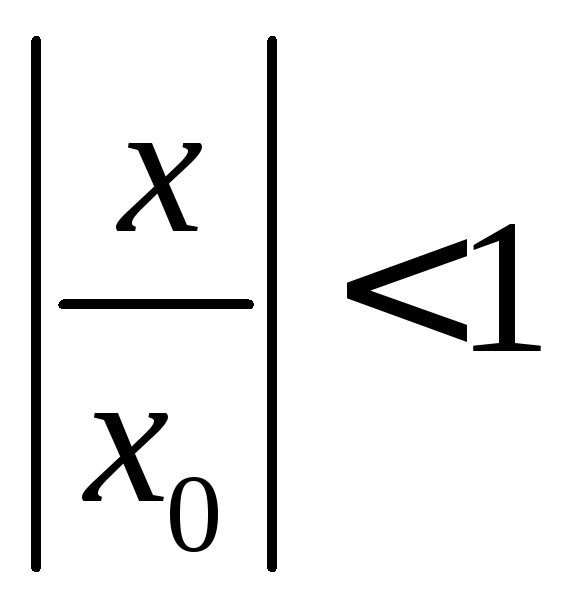, который сходится, поэтому сходится и ряд из модулей.

2. Пусть в точке ряд расходится. Тогда он будет расходится в любой точкехудовлетворяющей условию. Действительно, если бы в какой-либо точкеудовлетворяющей этому условию, ряд сходится, то в силу 1 он должен был бы сходится и в точке, т.к., что противоречит условию, что в точкеряд расходится .

Из теоремы Абеляследует, что если– точка сходимости, то весь интервалзаполнен точками абсолютной сходимости, т.е. существует число, такое что при всеххтаких, что- степенной ряд сходится, а при– расходится.

Теорема. Областью сходимости степенного ряда является интервал с центром в начале координат.

Определение.Интервалом сходимости степенного ряда называется такой интервал отдо, что для всякой точки, лежащей внутри интервала, ряд сходится абсолютно, для точек, лежащих вне него – расходится. Число– радиус сходимости степенного ряда.

На концах интервала (при и) вопрос о сходимости решается индивидуально для каждого ряда.

Для определения радиуса сходимости применяют признаки Даламбера и Коши длямодулейчленов ряда.

Для определения

используем признак Даламбера для модулей: . Если, то ряд сходится, если- расходится. Поэтому.

Аналогично, – по признаку Коши.

Пользоваться этими формулами следует осторожно, т.к. пределы часто не существуют. Например, если бесконечное множество коэффициентов обращается в нуль (т.е. ряд содержит члены только с четными или нечетными степенямих), то пользоваться этими формулами нельзя.

Пример.. По Даламберу:.,. Тогда при- ряд сходится, при– расходится. Радиус сходимости. При– ряд расходится.

Пример... Приряд сходится, т.е. при, при– расходится,, присходится, при– расходится.

14.3. Интегрирование и дифференцирование степенных рядов

1. Если степенной ряд (1) имеет интервал сходимости, то ряд(2), полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимостиипри, т.е. внутри интервала сходимости производная от суммы ряда равна сумме производных от членов ряда.

Замечание.Полученный ряд снова можно почленно дифференцировать и продолжать так сколько угодно раз.

2. Пусть дан ряд (1). Тогда , еслии х принадлежат интервалу сходимости. Т.е. если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме интегралов от членов ряда

Пример 1.Рассмотрим ряд(– это геометрическая прогрессия с). Почленно интегрируя, получим:. Поскольку ряд в правой части сходится прих = 1, то.

Пример 2.Найти сумму ряда. Умножим обе части нахи проинтегрируем от 0 дох:. Дифференцируя, находим, или.

Пример 3.Найти сумму ряда. Продифференцируем:(разложение в ряд Маклорена). Тогда. Чтобы найтиС, положим в исходном ряде и в последнем равенствех=0:, т.е., т.е..

Пример 4.Найти сумму ряда(1). Трижды продифференцируем (1):, (2);, (3);. Получим исходный ряд, т.е..

, ,, тогда.

Для вычисления ,,подставимв формулы (1), (2), (3):;, тогдаи. Тогда;или;;.

14.4. Ряды Тейлора и Маклорена.

Имеется формула Тейлорадля функции, имеющий производные довключительно, в окрестности точки:, где остаточный член,.

Если имеет производныевсех порядков в окрестности точки, то в формуле Тейлора числоможно брать сколь угодно большим. Допустим, что, тогда, переходя в формуле Тейлора к пределу при, получим справа бесконечный ряд,Тейлора:. Если в формуле ряда Тейлора положить, то получимряд Маклорена:.

Для каждой элементарной функции существуют и, такие, что в интервалеона разлагается в ряд Тейлора (или Маклорена).

Пример 1.Разложить в ряд Маклорена функцию.

, .,.

, .

.

Тогда:

Пример 2.Разложить в ряд Маклорена.

, , поэтому

Пример 3.Разложить в ряд Маклорена.

, ,,

, ,,и т.д., поэтому:

.

Приведем еще несколько основных разложений

,

,

, (найдено в пример 1 из 14.3)

(из разложения при, получаем, что.. Подставляя вместох(), получим, тогда.