
- •Электротехника и основы электроники
- •Цель и порядок выполнения работ
- •Подготовка к лабораторным работам
- •Работа 1. Поверка амперметра и вольтметра
- •Работа 2. Проверка основных законов электрической цепи
- •Работа 3. Цепь переменного синусоидального тока с последовательным соединением катушки и конденсатора. Резонанс напряжений.
- •Работа 4. Параллельное соединение индуктивности и емкости. Резонанс токов.
- •Работа 5. Исследование цепи трехфазного тока при симметричной и несимметричной нагрузках фаз. Соединение звездой и треугольником.
- •Библиографический список
- •Содержание
- •Электротехника и основы электроники.
- •308012, Г.Белгород, ул.Костюкова, 46.
Работа 4. Параллельное соединение индуктивности и емкости. Резонанс токов.
Ц r L
Рис. 4.1. Схема электрической цепи с параллельным
соединением элементов.
Пояснения к работе
Рассмотрим
параллельное соединение катушки,
обладающей индуктивным xL=ωL
и активным r
сопротивлениями, с конденсатором,
обладающим емкостным сопротивлением
![]() (рис. 4.2). При включении такой цепи под
напряжением U
в катушке возникает ток Iк.
(рис. 4.2). При включении такой цепи под
напряжением U
в катушке возникает ток Iк.

Рис. 4.2. Принципиальная схема параллельного
соединения r, xL, xc
![]() , (4.1)
, (4.1)
где
![]() — полное сопротивление катушки.
— полное сопротивление катушки.
Вектор тока будет отставать от вектора напряжения на угол φк:
![]() ;
; ![]() . (4.2)
. (4.2)
В конденсаторе возникает ток Ic:
![]() . (4.3)
. (4.3)
Вектор тока İc
будет опережать на 90˚
вектор
![]() ,
φс=
90˚. Вектор
общего тока на основании первого закона
Кирхгофа:
,
φс=
90˚. Вектор
общего тока на основании первого закона
Кирхгофа:
İ = İк + İс. (4.4)
Векторная диаграмма токов согласно (4.4) показана на рис.4.З
Вектор тока İк
проводим под углом φк
к вектору напряжения
![]() .
Из конца вектора тока İк
проводим вектор тока İс
под углом φс=90˚
к вектору
напряжения
.
Из конца вектора тока İк
проводим вектор тока İс
под углом φс=90˚
к вектору
напряжения
![]() (в сторону опережения). Сумма вектора
İк
и İс
даст вектор общего тока, отстающий на
угол φ
от вектора напряжения.
(в сторону опережения). Сумма вектора
İк
и İс
даст вектор общего тока, отстающий на
угол φ
от вектора напряжения.
Для аналитического определения общего тока I и угла φ разложим ток катушки Iк на активную составляющую Ia, совпадающую с напряжением U, и индуктивностью IL, отстающую на 90˚ от напряжения U.
 ;
;
 , (4.5)
, (4.5)
где g и bL – активная и индуктивная проводимости катушки:
 ;
; 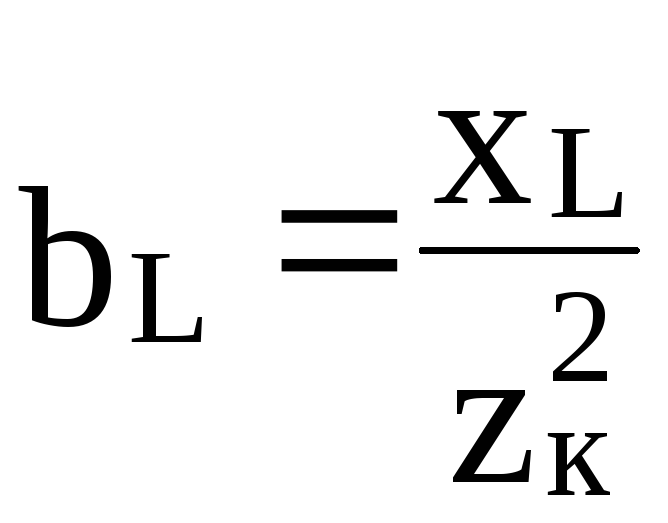 . (4.6)
. (4.6)
Аналогично
определяются проводимости конденсатора.
При отсутствии в конденсаторе активного
сопротивления (rc=
0) активная
проводимость его равна нулю:  , где
zc=
xc.
, где
zc=
xc.
Емкостная проводимость:
 (4.7)
(4.7)
Из векторной диаграммы на рис. 4.3. имеем:
![]() (4.8)
(4.8)
![]() . (4.9)
. (4.9)
Подставим значения Ia, IL и Ic из уравнения (4.5) и (4.7) в уравнение (4.8), получим:
![]() . (4.10)
. (4.10)
где ![]() – полная проводимость всей цепи.
– полная проводимость всей цепи.
Разделив стороны треугольника (рис.4.3) на напряжение U, получим треугольник проводимостей (рис.4.4), из которого находим:
![]() (4.11)
(4.11)
Изменяя величину емкости С, от которой зависит значение bc, согласно (4.7), можно изменять соотношение между bc и индуктивными проводимостями ( bL ), а, следовательно, и токами:
I
İс

![]()
Рис.4.3. Векторная диаграмма напряжения и токов для цепи с параллельным
соединением катушки и емкости при IL>IС
При
величине bC<bL, т.е. C<![]() имеем:
имеем:
Uωс<Ubc или IC<IL.
Преобладает
индуктивная проводимость bL
и, следовательно, ток IL,
поэтому вектор общего тока İ
отстает от вектора напряжения
![]() (рис.4.3).
(рис.4.3).
При
величине bC>bL, т.е. C>![]() имеем:
имеем:
Uωс<UbL или IL<IС
Преобладает
емкостная проводимость bC
и, следовательно, ток IС,
поэтому вектор общего тока İ
опережает вектор напряжения
![]() (рис.4.5).
(рис.4.5).


![]()

Рис.4.4. Векторная диаграмма для цепи с параллельным
соединением катушки и емкости при IC< IL

İк
Рис.4.5. Векторная диаграмма для цепи с параллельным
соединением катушки и емкости при IC> IL
При величине
емкости: ![]() , (4.12)
, (4.12)
емкостная проводимость равна индуктивной:
bC = ωc = bL, (4.13)
а, следовательно, будут равны между собою емкостный и индуктивный токи (рис.4.6):
bC U= bLU ; IC= IL. (4.14)
Мы получим резонанс токов, т.е. полную взаимную компенсацию индуктивного и емкостного токов:
IC – IL= 0. (4.15)
В результате общий ток I при резонансе состоит только из активной составляющей, согласно выражению (4.8) и рис.4.6.
I= Ia= Ug, (4.16)
поэтому угол φ= 0, а cos φ= 1.
Полная проводимость
цепи, а следовательно, и ток I
принимает минимальное значение, так
как согласно (4.10) У=g,
поскольку bC
– bL=
0,
а полное сопротивление цепи
![]() ,
следовательно максимальное значение.
,
следовательно максимальное значение.
Реактивная мощность цепи равна нулю:
U(IC - IL) = 0 ; QL – QC= 0.

![]()
Рис.4.6. Векторная диаграмма при резонансе токов (IC= IL)
Явление резонанса токов, т.е. взаимной компенсации реактивных токов (IC–IL=0), а, следовательно, и реактивных мощностей (QL–QC=0) объясняют следующим. Когда индуктивная ветвь (катушка) потребляет энергию для создания магнитного поля, в этот момент в параллельной ветви конденсатор разряжается и отдает энергию. Происходит взаимная компенсация энергий.
Общая энергия, потребляемая из сети, расходуется только на активном сопротивлении катушки (на нагревание провода катушки).
Зависимость полного сопротивления Z цепи от величины емкости будет иметь следующий вид:
![]() , (4.18)
, (4.18)
где
 и
и
 от C
не зависят.
от C
не зависят.
К ривыеZ=
f1(C)
и I=
f2(C),
построенные по выражениям (4.18) и (4.10),
показаны на рис.4.7. Там же дана кривая
cosφ=
f3(C),
построенная по уравнению (4.11). Из (4.12)
видно, что величины емкости и индуктивности,
при которых наступает резонанс, зависят
от частоты переменного тока. При заданных
постоянных C
и L
явление резонанса может быть получено
изменением частоты.
ривыеZ=
f1(C)
и I=
f2(C),
построенные по выражениям (4.18) и (4.10),
показаны на рис.4.7. Там же дана кривая
cosφ=
f3(C),
построенная по уравнению (4.11). Из (4.12)
видно, что величины емкости и индуктивности,
при которых наступает резонанс, зависят
от частоты переменного тока. При заданных
постоянных C
и L
явление резонанса может быть получено
изменением частоты.
C
Рис.4.7. График зависимости тока в цепи I, cosφ
и полного сопротивления z от емкости.
Определение параметров всей электрической цепи и ее элементов.
Полные проводимости У и сопротивление Z как всей цепи, так и отдельных ветвей – катушки и конденсатора, определяются по показаниям вольтметра V и соответствующих амперметров в общей цепи I, в цепи катушки Iк и в цепи конденсатора IL:
![]() ;
;  ;
;  .
.
Активное сопротивление
катушки r
определяется по показаниям ваттметра
P
и амперметра в цепи катушки Iк:  .
.
Тогда ![]() .
.
Коэффициент мощности cosφ всей цепи и катушки определяется по показаниям ваттметра P, вольтметра V и соответствующих амперметров, в общей цепи I и в цепи катушки Iк:
![]() ;
; ![]() .
.
Реактивные составляющие ток IL и проводимости катушки bL:
IL=
Iк
sinφк
;  .
.
Емкость конденсатора C:

Порядок выполнения работы
Собрать электрическую цепь по схеме, представленной на рис.4.8.

Рис.4.8. Схема электроустановки
Изменяя емкость (включением с помощью тумблера различных комбинаций конденсаторов), установить в цепи режим резонанса токов. Резонанс наступает при минимальном значении общего тока I=Iмин. Емкость, соответствующая резонансу, называется резонансной. Произвести измерение напряжения U, общего тока I, тока в ветви с индуктивностью Iк, тока в ветви с емкостью Ic и мощности P. Данные измерений занести в таблицу. Изменяя затем емкость на 0.5–2 мкф, произвести измерения для 4-х точек при емкостях меньших резонансной C0 и для 4-х точек при емкостях больших резонансной емкости.
Полученные данные свести в следующую таблицу 4.1.
Таблица 4.1
|
№ п/п |
Измерено |
Вычислено | ||||||||||||
|
U, B |
I, A |
IК, A |
IС, А |
rК, Ом |
Z, Ом |
P, Вт |
XС, Ом |
С, мкФ |
ZК, Ом |
cosφ |
ХL, Ом |
IL, А |
сosφк | |
|
1 2 … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По данным опыта определить параметры всей цепи (полное сопротивление Z и cosφ и её элементов, полное сопротивление катушки Zк, активное сопротивление катушки rк, коэффициент мощности катушки cosφк, реактивный ток IL, емкостное сопротивление xc и емкость С).
![]() ;
;![]() ;
;![]() ;
;![]() .
.
![]() ;
;  ;
; ![]() .
.
![]() ;
; ![]() .
.
По данным опыта и вычислений построить в масштабе зависимости
Z= f(C) ; I= f(C) ; cosφ= f(C)
Построить методом засечек векторные диаграммы токов для трех отсчетов:
при резонансе bL= bC
при bL> bC
при bL< bC
Контрольные вопросы.
Как и почему изменяется ток в цепи, содержащей индуктивную катушку, если параллельно катушки включить конденсатор?
Каким должно быть соотношение реактивных проводимостей катушки и конденсатора, чтобы ток в общей цепи опережал напряжение?
Каково условие резонанса токов?
Способ повышения коэффициента мощности с помощью конденсаторных батарей и его экономическое значение.
Почему при резонансе токов ток в общей цепи имеет наименьшее значение?
Н
 ачертить
векторную диаграмму, соответствующую
изображенной схеме:
ачертить
векторную диаграмму, соответствующую
изображенной схеме:
Н
I2
ачертить схему замещения, для которой изображена следующая векторная диаграмма:

I4
U
