4_Зубчатые передачи2

9

Зубчатые передачи

Зубчатая передача представляет из себя два колеса зубьями, посредством кото­рых они сцепляются между собой и передают вращение.

Меньшее зубчатое колесо передачи называется шес­терней, а большее - колесом.

Классификация

1. По расположению осей валов:

- передачи с параллельными осями. Сюда относят цилиндрические колеса внешнего и внут­реннего зацепления (это прямозубые, косозубые, шевронные, зацепление Новикова, волновые зацепления) (рис.1).

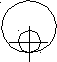
наружное зацепление внутреннее зацепление

Рис. 1.

- с пересекающимися осями. К ним относятся конические ко­леса (рис 2),

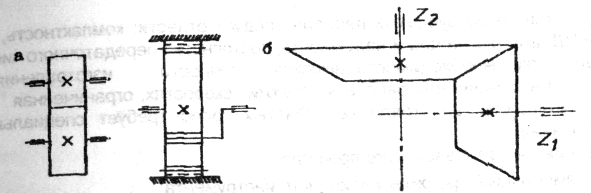
Рис. 2.

- с перекрещивающимися осями. Это червячные, винтовые и передачи между зубчатым колесом и рейкой (рис.3).

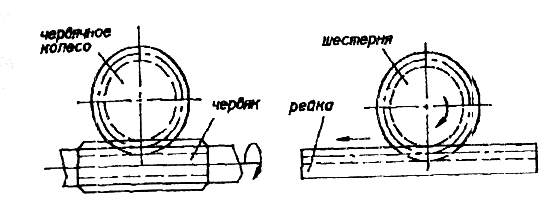
Рис. 3.

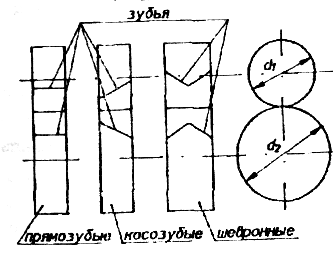2.По расположению зубьев на ободе колеса различают передачи: прямозубые, косозубые и шевронные (рис. 4).

Рис. 4.

3. По форме профиля зуба переда­чи подразделяются на эвольвентные и круговые (рис.5).

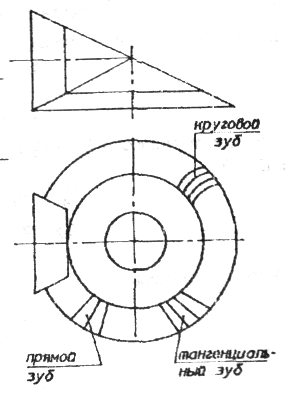
Рис. 5.

Наиболее рас­пространен эвольвентный профиль зуба, предложенный Эйлером в 1760 г. Он обладает рядом существенных технологических и эксплуатаци­онных преимуществ. Круговой профиль зуба предложен М.Л. Новиковым в 1954 г.

Достоинства зубчатых передач:

-компактность, высокий КПД, долговечность и надежность, постоянство передаточного числа.

Недостатки:

-необходимость высокой точности изготовления колеса, шум и вибрация при работе на высоких скоростях, ограниченная ремонтопригодность; изготовление зубчатых колес требует специального оборудования.

Элементы зубчатых передач

    Стандартом установлены все понятия, термины, определения и обозначения, а также методы расчета геометрических параметров зубчатых передач.

Основные параметры.

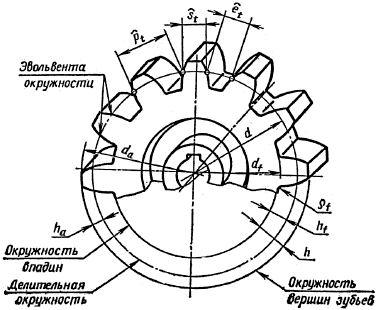
Рис. 5. (Упрощенное изображение цилиндрического прямозубого колеса).

   

В обозначениях параметров зубчатой передачи различают индексы, относящиеся:

ω — к на­чальной поверхности или окружности;

b — к основ­ной поверхности - или ок­ружности;

а — к поверх­ности или окружности вер­шин и головок зубьев;

f - к поверхности или окруж­ности впадин и ножек зубьев.

Параметрам, отно­сящимся к делительной по­верхности или окружности, дополнительного индекса не приписывают. Параметрам ше­стерни приписывают ин­декс 1, а параметрам ко­леса — 2.

Основными параметрами зубчатого колеса согласно ГОСТ 16531-70 являются:

d - диаметр делительной окружности;

d_а - диаметр окружности выступов;

d_f - диаметр окружности впадин;

P_f - окружной делительный шаг зубьев, представляющий собой расстояние между одноименными профилями соседних зубьев по дуге делительной окружности;

S_f - окружная толщина зуба;

e_f - окружная ширина впадины зуба;

h_a - высота головки зуба;

h_f - высота ножки зуба;

Z - число зубьев.

    Основным расчетным параметром зубчатого зацепления является модуль зацепления:

.

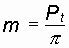    Так как длина делительной окружности πd = P_t Z, то d = m Z;     

.    Из этих уравнений следует два определения модуля:

• это линейная величина, в π раз меньшая окружного шага;

• это число миллиметров делительного диаметра, приходящихся на один зуб.

    Модуль является основным расчетным параметром зубчатой передачи. Его значения при проектировании выбирают из ГОСТ 9563-60.

Рекомендуемые значения модулей

Ряд	Модуль зацепления, (m), мм
1	1	1,25	1,5	2	2,5	3	4	5	6	8	10	12	16	20
2	1,125	1,375	1,75	2,25	2,75	3,5	4,5	5,5	7	9	11	14	18	22

Цилиндрические зубчатые колеса.

Зубчатые колеса для параллельных валов называют цилиндрическими. Одно из двух входящих в зацепление зубчатых колес – передающее движение – является ведущим, другое – ведомым.

Виды цилиндрических зубчатых колес.

Зубчатые колеса, зубья которых параллельны оси колеса, называются прямозубыми. Недостатком прямозубых передач является то, что зуб входит и выхо­дит из зацепления всей своей длиной.

Для увеличения контактной длины и числа зубьев, находящихся в зацеплении (что необходимо для передачи большего момента и более плавной работы на повышенных частотах вращения), применяют косозубые зубчатые колеса.

Пре­имущества косозубых зубчатых колес по сравнению с прямозубыми: лучшая прирабатываемость зубьев, меньший шум и динамические нагрузки, большая несущая способность. Недостатком косозубых колес является осевое усилие, возникающее в контакте зацепленных зубьев. Для его устранения применяются шевронные зубчатые колеса с V-образными (угловыми) косыми зубьями.

 (На практике: Прямозубые зубчатые передачи: Основная теорема зацепления; основные параметры – эвольвента, основная, делительная окружность, линия зацепления; влияние угла зацепления, числа зубьев и высоты головки зуба на работу передач; исходный контур на зубчатый профиль – рейка; коррегирование; степени точности зубчатых колес; инструменты, для нарезания колес с различной степенью точности).

Геометрические параметры косозубых зубчатых колес.

У косозубых колес зубья располага­ются не по образующей делительного цилиндра (как у прямозубых), а составляют с ней некоторый угол β (рис.). Оси колес при этом остаются параллельными. Для нарезания косых зубьев используют инструмент такого же исходного контура, как и для нарезания прямых. Поэтому профиль косого зуба в норм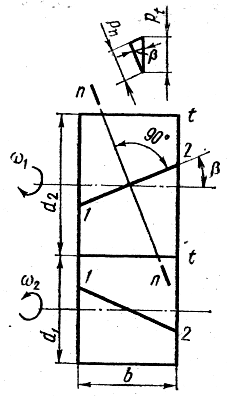альном сечении n—n совпадает с профилем прямого зуба. Мо­дуль в этом сечении должен быть также стандартным (см. табл.). В торцовом сечении t — t параметры косого зуба изменяются в зави­симости от угла β:

- окружной шаг p_t = p_n/cosβ,

- окружной модуль m_t = m_n/cosβ, (стандартным является нормальный модуль),

- делительный диаметр d= m_t z= m_nz/cosβ.

Индексы n и t приписывают параметрам в нормальном и торцовом сечениях соответственно.

Для косозубых колёс аналогичны все формулы по коррегированию, что и для прямозубых.

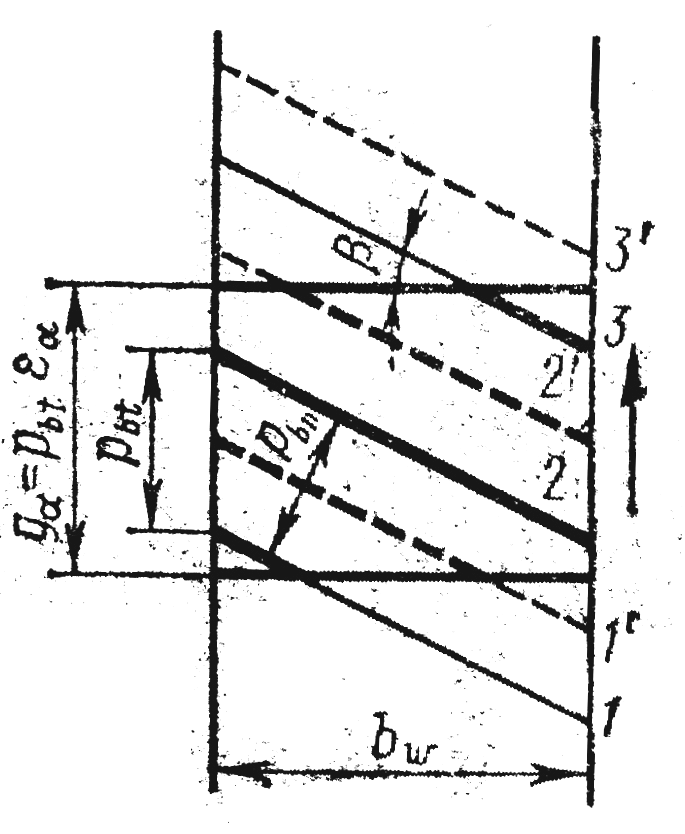
Межосевое расстояние пары косозубых колес

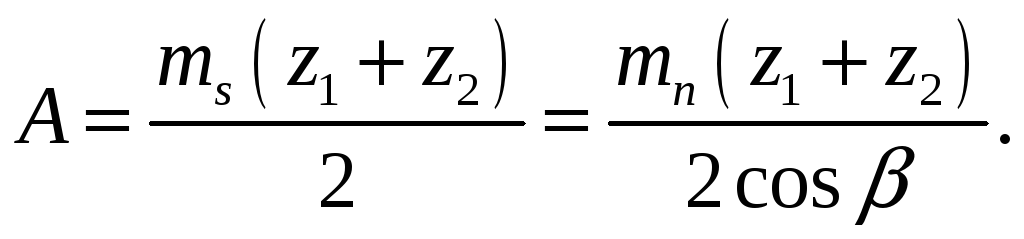
Эквивалентные колеса.

Расчет косозубых колёс обычно сводится к расчету прямозубых, которые заменяются соответствующим эквивалентным колесом.

Рассечем косозубое колесо нормальной плоскостью, в сечении получим эллипс.

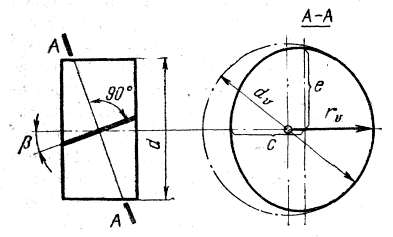
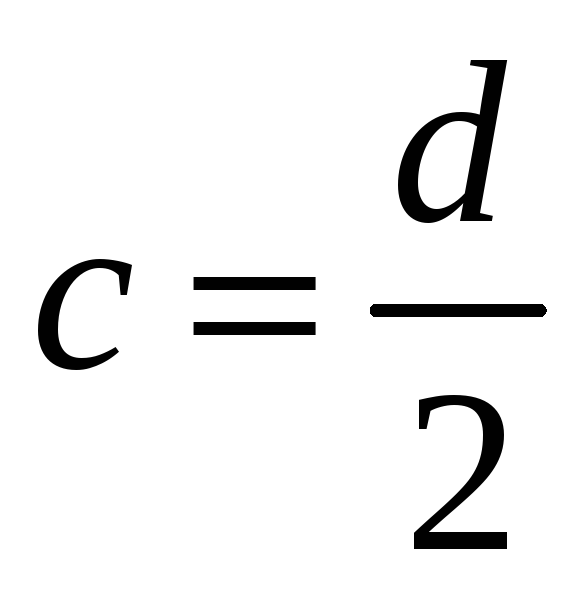
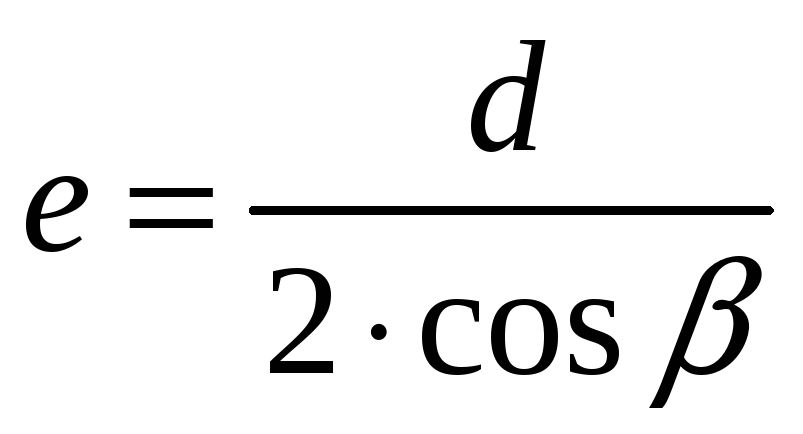
Из математики – радиус кривизны эллипса по малой оси

,

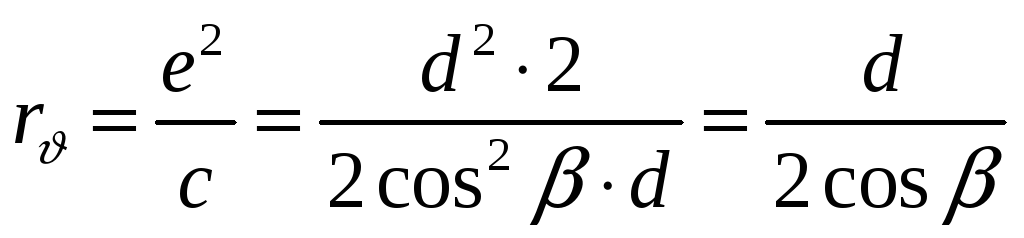Следовательно, диаметр эквивалентного колеса d_э будет равен:

.

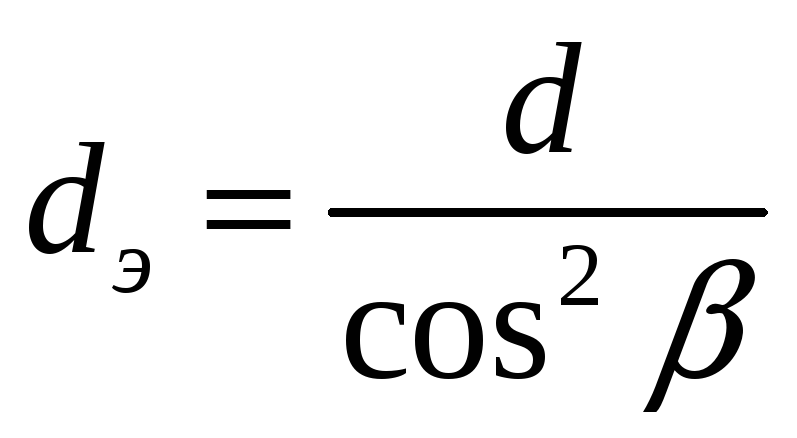Число зубьев эквивалентного колеса z_э:

.

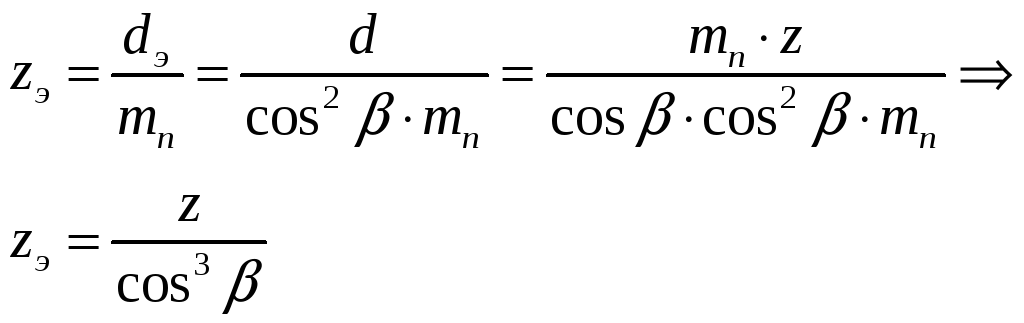По значениям z_э по таблицам находят коэффициент y_f , учитывающий форму зуба. y_f используется при проверке зубьев на выносливость при изгибе.

Увеличение эквивалентных параметров (d_э и z_э) с увеличением угла β является одной из причин повышения прочности косюзубых передач. Вследствие наклона зубьев получается колесо как бы больших разме­ров или при той же нагрузке уменьшаются габариты передачи.

В отличие от прямых - косые зубья вхо­дят в зацепление не сразу по всей длине, а постепенно. В прямозубом же зацеплении на­грузка с двух зубьев на один или с одного на два передаются мгновенно. Это явление сопровождается ударами и шумом. В косозубых передачах зубья нагружаются постепенно по мере захода их в поле зацепления и в зацеплении всегда находится минимум две пары. Плавность косо­зубого зацепления значительно понижает шум и дополнительные ди­намические нагрузки.

Данное преимущество косозубого зацепления особенно значительно в быстроходных передачах, так как динамические нагрузки возрастают пропорционально квадрату скорости.

Усилия зацепления:

а) Прямозубые передачи.

Усилия выражают через окружную силу ;

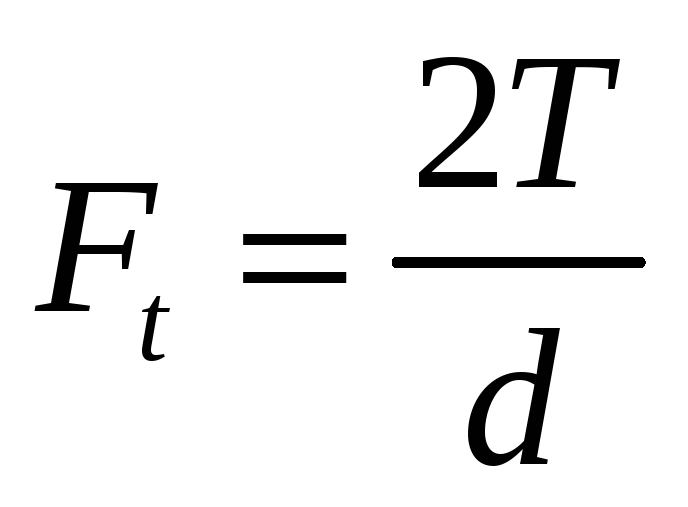- нормальная сила, действующая по линии зацепления;

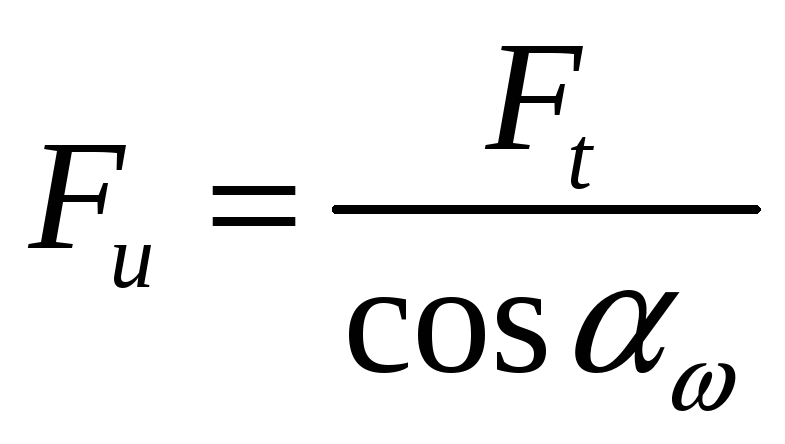-радиальная сила;

- нормальная сила.

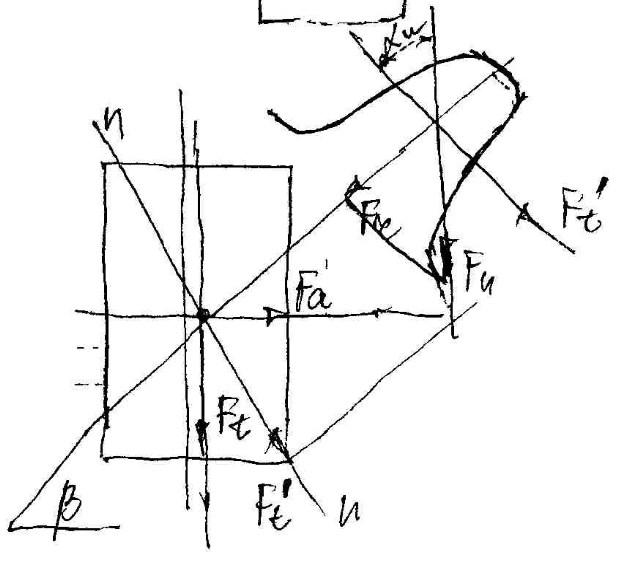
б) Косозубые передачи.

Рассечем косозубое колесо нормальной плоскостью n-n. В сечении получим зуб прямозубого эквивалентного колеса.

Окружная сила ;

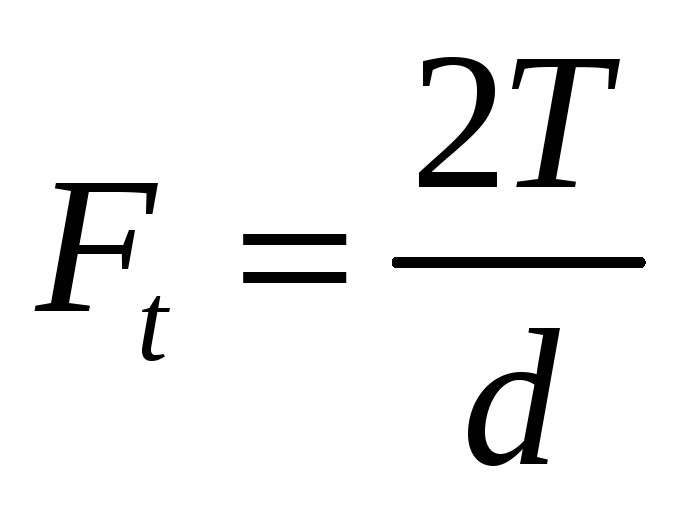Осевая сила .

С увеличением β резко увеличивается осевая сила, что неблагоприятно действует на подшипники качения. Поэтому в косозубых передачах для уменьшения нагрузки на подшипники принимают:

β=8⁰, 10⁰ …20⁰.

В шевронных передачах β=250, 300,400, т.к. осевые силы взаимно уничтожаются.

Радиальная сила: