1.2.Скорость

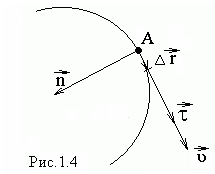
В физике под скоростью понимают векторную величину, характеризующую быстроту перемещения материальной точки по траектории и направление движения в каждый момент времени. Разобьем траекторию на бесконечно малые участки длины (рис.1.4), каждому из этих участков сопоставим бесконечно малое перемещение. Разделив это перемещение на соответствующий промежуток времени, получим мгновенную скорость в данной точке траектории:

. (1.3)

Таким образом, скорость есть первая производная радиус-вектора точки по времени. Перемещение совпадает с бесконечно малым элементом траектории, следовательно векторнаправлен по касательной к траектории ( рис.1.4).

Разложив вектор скорости по базису системы координат, получаем:

, где - проекции векторана координатные оси. Модуль вектора скорости равен.

Можно показать, что модуль скорости равен производной пути по времени:

Движение называется равномерным, если вектор скорости остается постоянным по величине и направлению. В противном случае говорят о переменном движении.

В соответствии с формулой (1.3), элементарное перемещение материальной точки . Тогда перемещение из положения 1 в положение 2 (рис.1.2) равно интегралу

Пройденный путь определяется выражением .

Среднее значение модуля скорости за время от доравноСредний вектор скорости.

Вектор скорости можно представить в виде

, (1.4)

где – модуль скорости,– орт вектора. Введем орт касательной к траектории, условившись направлять его в ту же сторону, что и. Тогда, очевидно, ортыисовпадут, и можно записать

Подставив в выражение (1.3) радиус-вектор в виде , получаем

.

Для простоты рассуждений будем считать траекторию плоской кривой, лежащей в плоскости ( рис.1.5). В записанной формуле первая составляющая вектора скоростинаправлена вдоль радиус-вектораи характеризует быстроту изменения модуля. Вторая составляющая равнаи характеризует быстроту изменения радиус-вектора по направлению.

Из математики известно: , где– угол между радиус-вектором и осью,– перпендикулярный к радиус-вектору орт, направленный в сторону возрастания угла. Подставивв формулу для, получаем

.

Таким образом, составляющая и соответствующий ортсвязаны с изменением угла.

Очевидно, что векторы ивзаимно перпендикулярны, следовательно

1.3.Ускорение

Быстрота изменения вектора скорости называется ускорением материальной точки и определяется производной векторапо времени:

. (1.5)

Cпроектируем это выражение на координатные оси: .

Подставив в формулу (1.5) выражение (1.4), получаем:

.

Продифференцировав, имеем: .

Следовательно, вектор можно представить в виде суммы двух взаимно перпендикулярных составляющих (рис.1.6). Первая направлена по касательной к траектории и называется тангенциальным или касательным ускорением

. (1.6)

Вторая составляющая направлена по , т.е. перпендикулярно касательной, по нормали к траектории, и называется нормальным ускорением.

Исследуем свойства обеих составляющих, ограничившись случаем плоского движения. Модуль тангенциального ускорения, как следует из (1.6), равен . Если(скорость растет по величине), векторнаправлен в ту же сторону, что и( т.е. в ту же сторону, что и). Если(скорость со временем уменьшается), векторыинаправлены противоположно. При равномерном движении.

Нормальное ускорение определяется величиной , т.е. быстротой изменения во времени направления касательной к траектории. Эта быстрота будет тем больше, чем сильнее искривлена траектория и чем быстрее перемещается частица по траектории.

Степень искривления плоской кривой характеризуется кривизной С, которая определяется выражением

где –угол между касательными к кривой в точках, отстоящих друг от друга на расстояние(рис.1.7). Таким образом, кривизна определяет скорость поворота касательной при перемещении вдоль кривой. Величина, обратная кривизнеС, называется радиусом кривизны в данной точке

Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом ее участке. Центр такой окружности называется центром кривизны для данной точки кривой.

Радиус и центр кривизны в точке 1 (рис.1.7) определим следующим образом. Возьмем вблизи точки 1 точку 1. Построим в этих точках касательные и, перпендикуляры к которым пересекутся в некоторой точкеО. При этом для кривой, не являющейся окружностью, расстояния  и  несколько отличаются друг от друга. Если точку 1 приближать к точке 1, пересечение перпендикуляров O будет перемещаться вдоль прямой  и в пределе окажется в некоторой точке О. Эта точка и будет центром кривизны для точки 1. Расстояния R и R будут стремиться к общему пределу , равному радиусу кривизны.

Как известно из математики, (1.7)

Здесь – орт нормали к траектории, направленный в сторону поворота векторапри движении частицы по траектории. Величинуможно связать с радиусом кривизны траектории и скоростью частицы. Из рис. 1.7 следует, чтогде- угол поворота вектораза время(совпадающий с углом между перпендикулярами и ), - средняя скорость на пути. Отсюда. В пределе при 0 приближенное равенство станет строгим, средняя скорость превратится в мгновенную скоростьв точке 1,- в радиус кривизны . В результате получится равенство

(1.8)

- быстрота поворота вектора скорости пропорциональна кривизне траектории и скорости перемещения частицы по траектории.

Подставив (1.7) в формулу (1.8), получим , тогда нормальное ускорение равно .

Вектор ускорения при движении материальной точки по плоской кривой равен , а его модуль

При прямолинейном движении нормальное ускорение отсутствует. Интересным является тот факт, что обращается в ноль в точке перегиба криволинейной траектории (точка ТП на рис.1.8). По обе стороны от этой точки векторынаправлены в разные стороны. Векторне может изменяться скачком, изменение направления на противоположное происходит плавно с обращениемв ноль в точке перегиба.

Если материальная точка движется с постоянными по величине скоростью и ускорением, то , так чтои, поэтому– частица движется по линии постоянной кривизны, т.е. по окружности.