3.7.Сила ампера

Ампер исследовал действие магнитного поля на проводники с током и показал, что сила F, действующая на прямолинейный проводник с током, находящийся в однородном магнитном поле, прямо пропорциональна силе тока I в проводнике, его длине , магнитной индукциии синусу угламежду направлениями тока в проводнике и вектором:

.

В случае неоднородного магнитного поля и проводника произвольной формы перейдем к бесконечно малым приращениям, имеем:

.

-коэффициент пропорциональности, зависящий от выбора единицы измерения. В СИ .

Будем считать, что элемент проводника перпендикулярен вектору, тогда

-магнитная индукция численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет электрический ток единичной силы и который расположен перпендикулярно к направлению магнитного поля. Т.е. магнитная индукцияявляется силовой характеристикой поля.

Направление силы определяется по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению электрического тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник со стороны поля.

Если не перпендикулярен, то векторсовпадает по направлению с векторным произведением- векторнаправлен перпендикулярно к плоскости, образованной векторамиитаким образом, чтобы из конца векторавращение от векторак векторупо кратчайшему пути происходило против часовой стрелки.

Закон Ампера в векторной форме имеет вид:

.

Силы электромагнитного взаимодействия не являются центральными и всегда перпендикулярны к линиям магнитной индукции.

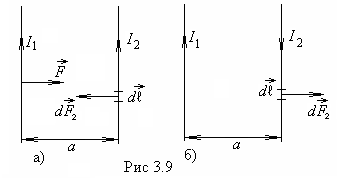Рассмотрим два длинных прямолинейных проводника, которые расположены параллельно друг к другу. Расстояние между проводниками а. При пропускании тока по проводникам между ними возникает сила взаимодействия. Рассмотрим некоторые частные случаи.

1.Пусть токи ив проводниках направлены в одну сторону (рис.3.9а). В этом случае проводники притягиваются друг к другу. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на другой проводник. При этом на элементвторого проводника с токомдействует сила:

.

Если а << , то проводник можно считать бесконечно длинным, тогда

, при этом ,, имеем.

Для выражение примет такой же вид. Оно симметрично для обоих проводников, поэтому

, тогда .

2. Если токи противоположны по направлению, то проводники отталкиваются (рис.9б).

Единицы измерения в системе СИ: магнитная индукция - B=[Тл] – тесла; напряженность магнитного поля H=[] - ампер на метр.

3.8. Сила лоренца

Экспериментально было установлено, что пучок электронов, испускаемых катодной трубкой, отклоняется во внешнем магнитном поле. Направление отклонения перпендикулярно к вектору индукции и векторускорости упорядоченного движения электронов. Таким образом, на заряды, движущиеся в магнитной поле, действует сила, направление которой совпадает с направлением векторного произведения, если частицы отрицательно заряженные, или, если частицы заряжены положительно.

Определим силу, действующую на электрический заряд, движущийся в магнитном поле. По закону Ампера на элемент проводника с токомI, действует сила

.

Ток в проводнике определяется движением зарядов, которые движутся со скоростью :, гдеdn - число частиц в элементе проводника ,.

Определим силу, действующую на один заряд:

-

- это сила Лоренца. Направление определяется знаком зарядаq. Сила Лоренца всегда направлена перпендикулярно к скорости движения заряда и играет роль центростремительной силы. Сила Лоренца не совершает работы. Она изменяет только направление скорости движения заряда в магнитном поле. Абсолютная величина скорости заряда и его кинетическая энергия при движении в магнитном поле не изменяется

.

Но неизменность величины скорости и кинетической энергии заряженной частицы имеет место лишь в случае постоянного магнитного поля, не зависящего от времени, т.е. стационарного. Переменное же магнитное поле ускоряет заряженные частицы (т.е. меняет величину и направление скорости).

Рассмотрим движение частицы в однородном магнитном поле. Будем считать, что на частицу не действуют никакие электрические поля.

1. Пусть частица движется вдоль линий индукции магнитного поля (рис.3. 10), тогда угол м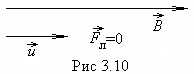ежду векторамии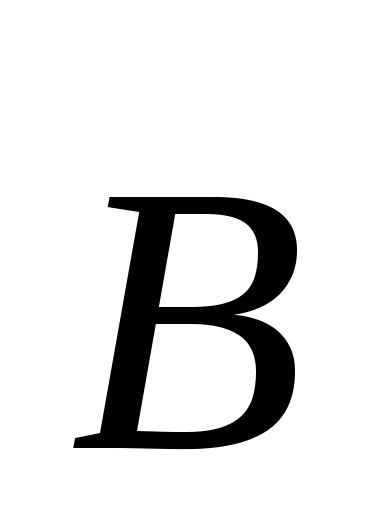равен 0 или,,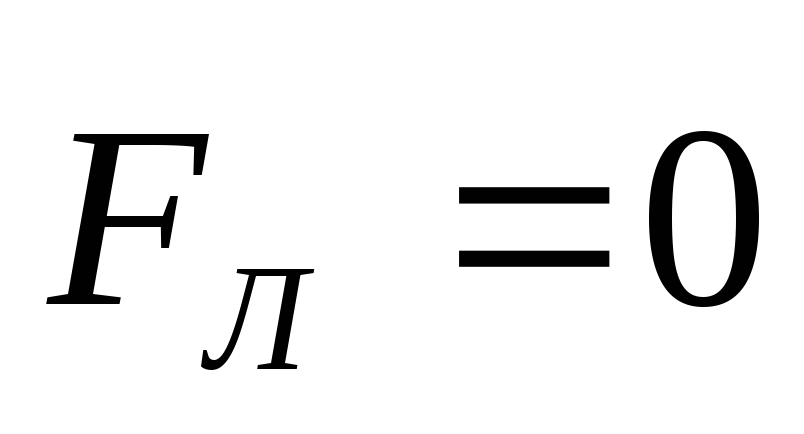 т.е. магнитное поле не действует на частицу. Она будет двигаться по инерции – прямолинейно и равномерно.

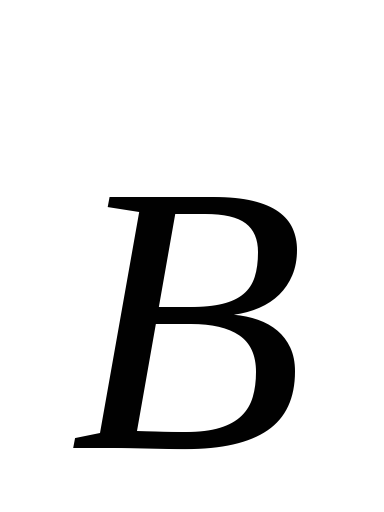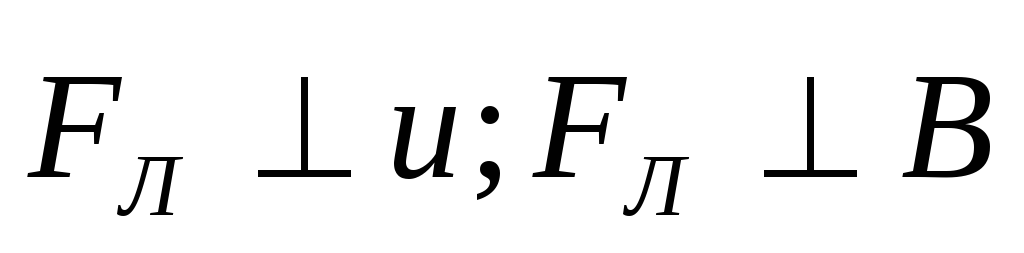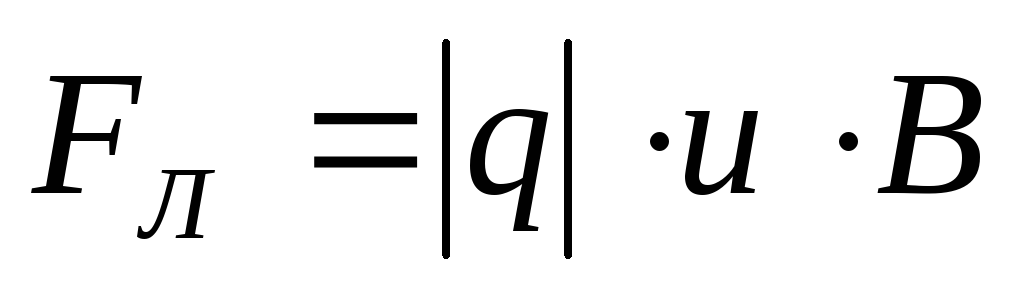2. Рассмотрим теперь частицу, которая движется перпендикулярно к линиям магнитной индукции(рис.3. 11): _и . В этом случае частица движется в плоскости, перпендикулярной к вектору магнитной индукции, и сила Лоренца является центростремительной силой:

,

где m – масса заряженной частицы, r – радиус кривизны ее траектории. Найдем r:

.

Скорость частицы не меняется, индукция =const, значит, r=const, и заряженная частица будет двигаться по окружности, плоскость которой перпендикулярна к магнитному полю.

Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависит от знака зарядаq. Поэтому по направлению отклонения можно судить о знаке заряда.

Частица движется в магнитном поле по окружности радиуса r равномерно. Период обращения, т.е. время одного полного оборота:

- период обращения частицы не зависит от ее скорости. Этот период прямо пропорционален индукции магнитного поля.

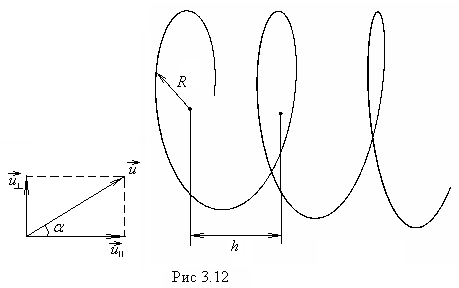3. Рассмотрим более общий случай, когда скорость частицы направлена под произвольным острым угломк вектору(рис.3.12). Разложим векторна две составляющие:

- параллельную вектору - и перпендикулярную к -:

.

Скорость в магнитном поле не меняется, это скорость поступательного движения частицы. Благодаря же скоростичастица движется по окружности в плоскости, перпендикулярной к, тогда радиус этой окружности:

.

Таким образом, частица одновременно совершает два движения – поступательное со скоростью в направлении поля, т.е. перпендикулярном к скорости вращения, и вращательное. При этом траекторией движения будет винтовая линия, ось которой совпадает с линией индукции магнитного поля, радиус витков

.

Шаг винта .