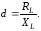- •Идеальные и реальные источники напряжения и тока, условия согласования с нагрузкой. Зависимости мощности и кпд от нагрузки.
- •Синусоидальный ток в резистивном двухполюснике- связь между током и напряжениями, векторная диаграмма.
- •5. Синусоидальный ток в индуктивном двухполюснике (идеальном и реальном) – связь между током и напряжениями, векторная диаграмма.
- •Последовательный окк – общие соотношения, векторные диаграммы, резонанс, ток и напряжения при резонансе.
- •3.2.5. Полоса пропускания
- •3.3.2. Параллельный колебательный контур с диссипацией в реактивных ветвях
- •Параллельный контур без диссипаций в реактивных ветвях – ачх и фчх, полоса пропускания.
- •3.3.2. Параллельный колебательный контур с диссипацией в реактивных ветвях
- •Коэффициенты связи двух связанных контуров – при индуктивной, автотрансформаторной и емкостной связей (внутри емкостная связь, внешне емкостная связь).
- •4.3.1. Коэффициент связи индуктивно связанных контуров
- •4.3.2. Коэффициент связи при автотрансформаторной связи контуров
- •4.3.3. Коэффициент связи при емкостной связи контуров
- •Эквивалентный контур для двух индуктивно связанных контуров.
- •Резонансная частота эквивалентного контура для двух индуктивно связанных контуров.
- •Уравнение резонансной кривой для двух индуктивно связанных контуров.
5. Синусоидальный ток в индуктивном двухполюснике (идеальном и реальном) – связь между током и напряжениями, векторная диаграмма.
Синусоидальный ток в индуктивном двухполюснике
Индуктивный двухполюсник представляет собой катушку индуктивности, к которой приложено напряжение. Если катушка индуктивности имеет мало витков и намотана проводом большого диаметра, а материал провода имеет малое удельное сопротивление, то ее омическое (резистивное) сопротивление очень мало, и в ней практически отсутствуют потери мощности сигнала. Такие индуктивные двухполюсники практически считаются идеальными.
Когда катушка имеет большое число витков и намотана проводом малого диаметра, то ее омическое сопротивление велико. Потери мощности в таких индуктивных двухполюсниках заметны и проявляются в нагреве катушек индуктивности. В схемах таких индуктивных двухполюсников вводится резистор, учитывающий омическое сопротивление катушки индуктивности и другие потери в ней. Такой индуктивный двухполюсник называется реальным.
Рассмотрим отдельно идеальный и реальный индуктивные двухполюсники.
Идеальный индуктивный двухполюсник характеризуется отсутствием явления диссипации, т. е. в нем не происходит рассеивание мощности. Его схема замещения содержит только катушку индуктивности (рис. 2.11). К двухполюснику приложено напряжение:


В комплексной форме оно имеет вид:
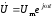 .
.
Напряжение на катушке индуктивности связано с током следующим соотношением:

При известном входном напряжении и известных параметрах катушки индуктивности неизвестным является ток ‑ его амплитуда и фаза. Из последнего уравнения определим ток:
 (2.53)
(2.53)
В комплексной форме это интегральное уравнение имеет вид:
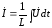 .
.
Подставим в это уравнение выражение напряжения в комплексной форме и найдем ток:
 (2.54)
(2.54)
Как отмечалось ранее, деление комплексной величины на j эквивалентно изменению фазы этой комплексной величины на 2. С учетом этого комплексная форма тока в идеальном индуктивном двухполюснике принимает вид:
 (2.55)
(2.55)
где

В вещественной форме выражение для тока имеет вид:
 (2.56)
(2.56)
Из выражений для тока видно, что в идеальном индуктивном двухполюснике ток отстает по фазе от напряжения на угол /2. На рис. 2.12, а показаны осциллограммы напряжения и тока, а на рис. 2.12, б показана векторная диаграмма этих же напряжений и токов. Комплексное сопротивление идеального индуктивного двухполюсника, в соответствии с (2.8), имеет вид:
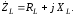 (2.57)
(2.57)

Выражение
для

 можно найти с помощью закона Ома, при
этом ток возьмем в виде (2.54):
можно найти с помощью закона Ома, при
этом ток возьмем в виде (2.54):
 (2.58)
(2.58)
Приравнивая правые части (2.57) и (2.58), делаем вывод, что
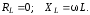 (2.59)
(2.59)
Окончательно
комплексное сопротивление идеального индуктивного двухполюсника
имеет вид:
идеального индуктивного двухполюсника
имеет вид:
 . (2.60)
. (2.60)
Мгновенная
мощность
идеального индуктивного двухполюсника
определяется по формуле (2.11), при
 :
:

Величина средней мощности определяется из известного выражения (2.17) и равна:
 .
.
 Из
этого следует вывод, что идеальный
индуктивный двухполюсник не потребляет
мощность. Это видно и из графика мгновенной
мощности (рис. 2.13) - в течение интервала
0/2
мощность потребляется, а в течение
интервала /2
мощность отдается. При этом площади,
ограниченные графиком мгновенной
мощности на этих интервалах равны.
Из
этого следует вывод, что идеальный
индуктивный двухполюсник не потребляет
мощность. Это видно и из графика мгновенной
мощности (рис. 2.13) - в течение интервала
0/2
мощность потребляется, а в течение
интервала /2
мощность отдается. При этом площади,
ограниченные графиком мгновенной
мощности на этих интервалах равны.
Добротность идеального индуктивного двухполюсника находим в соответствии с (2.23). Как видно из мгновенной мощности, амплитуда реактивной мощности равна:

 .
.
Тогда выражение для добротности принимает вид:
 .
.
Затухание идеального индуктивного двухполюсника, как обратная величина добротности, равно нулю:
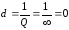 .
.
Реальный индуктивный двухполюсник представляет собой катушку индуктивности с потерями (диссипацией). Эти потери определяются как омическим сопротивлением провода обмоток катушки, так и электромагнитными потерями (потерями в магнитопроводе, за счет потока рассеивания). В схеме двухполюсника все эти потери отображаются введением в схему резистора. Наиболее широко применяется последовательная схема реального индуктивного двухполюсника (рис. 2.14).
К двухполюснику приложено напряжение:

 .
.
В комплексной форме оно имеет вид:
 .
.
Комплексное сопротивление двухполюсника, в соответствии с (2.8), равно:
 .
.
Представим его в показательной форме:
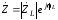 , (2.61)
, (2.61)
где  .
.
Ток в реальном индуктивном двухполюснике определяется из закона Ома в комплексной форме:
 , (2.62)
, (2.62)
где  .
.
В вещественной форме ток имеет вид:
 (2.63)
(2.63)
Напряжение на RL находим так же с помощью закона Ома:
 (2.64)
(2.64)
где  .
.
Аналогично находим напряжение на катушке индуктивности:
 (2.65)
(2.65)
где 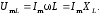
Появление (+/2) в фазе связано с тем, что умножение комплексного выражения на комплексную величину j эквивалентно изменению фазы этого комплексного выражения на (+/2).На рис. 2.15, а представлена векторная диаграмма для реального индуктивного двухполюсника. Здесь
 необходимо
обратить внимание на то, что угол L
близок по величине к /2,
т. к. RL<<XL.
Из последнего следует, что модуль
напряжения на индуктивности больше
модуля напряжения на резисторе. Рассмотрим
мощности в реальном индуктивном
двухполюснике. Мгновенная мощность
определяется в соответствии с (2.11):
необходимо
обратить внимание на то, что угол L
близок по величине к /2,
т. к. RL<<XL.
Из последнего следует, что модуль
напряжения на индуктивности больше
модуля напряжения на резисторе. Рассмотрим
мощности в реальном индуктивном
двухполюснике. Мгновенная мощность
определяется в соответствии с (2.11):
 (2.66)
(2.66)
Величина средней мощности, потребляемой реальным индуктивным двухполюсником, определяется в соответствии с (2.17) и (2.18):

Исходя из треугольника сопротивлений (рис. 2.15, б), имеем:


Учитывая это и выражение для амплитуды тока (2.62), выражение для средней мощности принимает вид:
 (2.67)
(2.67)
Добротность реального индуктивного двухполюсника находим по формуле (2.23):
 (2.68)
(2.68)
Затухание в реальном индуктивном двухполюснике определяется очевидным выражением: