5.11.Энергия электромагнитного поля. Плотность и поток энергии. Закон изменения энергии

Найдем энергию электромагнитного поля по заданным значениям векторов и. Для этого используем уравнения Максвелла

Умножим первое уравнение на , второе – наполучаем

Из равенства (5.28) вычтем (5.29), имеем

(5.30)

Из математики известно, что

Левая часть выражения (5.30) есть частная производная по времени от функции Тогда имеем:

или

Проинтегрируем это выражение по объему V:

Преобразуем: Получаем

(5.31)

Но - работа поля за единицу времени в пределах конечного объемаV. Тогда- плотность энергии электромагнитного поля. Она равна сумме плотностей энергий электрического и магнитного полей.- плотность потока энергии, называемая вектором Пойтинга. Этот вектор направлен в сторону перемещения энергии и по абсолютному значению равен энергии, которая в единицу времени переносится полем через единичную площадку, ориентированную перпендикулярно потоку.

Тогда энергия поля в заданном объеме Vравна

Поток энергии поля через замкнутую поверхность в единицу времени определяет полную мощность излучения системы зарядов и равен

Таким образом, равенство (5.31) – это математическое выражение закона изменения энергии электромагнитного поля. Его можно переписать в виде:

(5.32)

(W не зависит от координат точек поля и частную производную можно заменить полной). Теорема (5.32) читается так:убыль энергии в некотором объеме равна потоку энергии, выходящему из объема, и работе , совершаемой полем над зарядами в этом объеме.В дифференциальной форме эта теорема имеет вид:

В области, где нет зарядов и токов (), плотность электромагнитной энергии связана с ее потокомуравнением непрерывности:

(5.33)

Это уравнение является локальным выражением закона сохранения энергии для электромагнитного поля при отсутствии зарядов. Оно выражает теорему Пойтинга.

Проинтегрируем (5.33) по объему V, ограничивающему поверхностьs:

Таким образом, при отсутствии зарядов убыль энергии поля в объеме V в единицу времени равна интегральному потоку энергии через поверхность, ограничивающую этот объем.

Если потока энергии через границы поля нет, , и энергия поля убывает, если- заряды движутся под действием сил поля. Если же, то энергия поля растет, но в этом случае работают не силы поля, а сторонние силы, не сводящиеся к силе Лоренца.

5.12. Закон сохранения энергии для изолированной системы поле – заряды

Рассмотрим изолированную систему поле-заряды. Изолированность системы следует понимать как отсутствие потока энергии через ограничивающую ее поверхность и отсутствие потока массы , который тоже уносил бы энергию. В таком случае убыль энергии электромагнитного поля в единицу времени равна

• работе, совершаемой полем над зарядами.

Ясно, что работа, производимая над зарядами, является мерой превращения энергии поля в другие виды: в кинетическую энергию заряженных частиц и тел, потенциальную энергию деформации, внутреннюю энергию среды и т.д. Для дискретной системы зарядов

тогда подставляя в (5.31) выражение (5.25), получаем

.

Из этого выражения следует, что

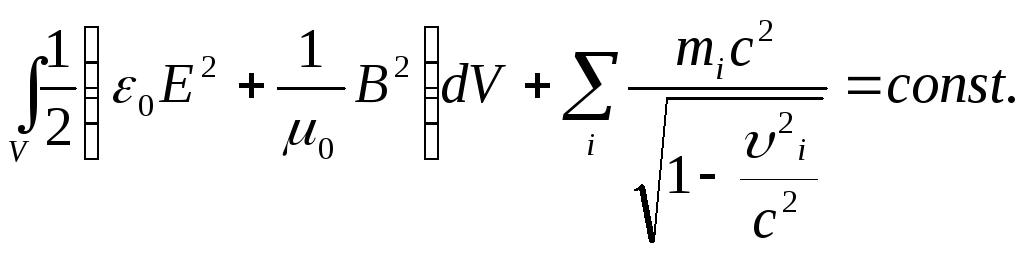
В последнем равенстве объем Vможет быть или конечным, или охватывать все пространство. Это соотношение выражает закон сохранения энергии в изолированной системе поле-заряды:в изолированной системе поле-заряды сохраняется сумма энергии поля и релятивистской энергии заряженных материальных точек.