
- •5. Механика твердого тела
- •5.1 Движение твердого тела
- •5.2. Движение центра масс твердого тела
- •5.3. Вращение тела вокруг неподвижной оси
- •5.4. Момент инерции
- •5.5. Гироскопы
- •5.6. Кинетическая энергия вращающегося твердого тела
- •5.7. Кинетическая энергия при плоском движении
- •5.8. Условия равновесия твердого тела
5.6. Кинетическая энергия вращающегося твердого тела
Р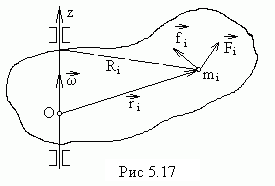 ассмотрим
вращение тела вокруг неподвижной оси
ассмотрим
вращение тела вокруг неподвижной оси![]() (рис.5.17).
(рис.5.17).
Линейная
скорость элементарной массы![]() равна
равна![]() ,
,
где
![]() -расстояние массы
-расстояние массы
![]() до
оси
до
оси![]() .
.
Кинетическая
энергияэтой элементарной массы![]()
Кинетическая энергия тела равна сумме кинетических энергий всех его частиц
![]()
Сумма
в правой части этого равенства есть
момент инерции тела относительно оси
![]() .
.
Тогда
![]()
Если на массу
![]() действуют
внутренняя сила
действуют
внутренняя сила![]() и внешняя сила
и внешняя сила![]() (рис.5.13),
то работа этих сил за время
(рис.5.13),
то работа этих сил за время![]() равна
равна![]()
Преобразовав,
получаем
![]() (5.8)
(5.8)
![]() - момент
внутренней силы относительно точкиО,
- момент
внутренней силы относительно точкиО,
![]() - момент внешней
силы.
- момент внешней
силы.
Просуммировав равенство (5.8) по всем элементарным массам, получим
работу,
совершенную над телом за время
![]() :
:
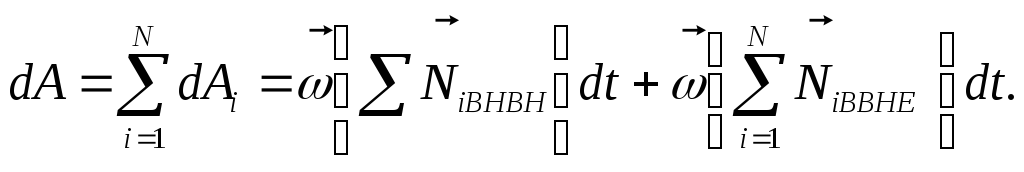
Сумма моментов всех внутренних сил равна нулю, тогда работа
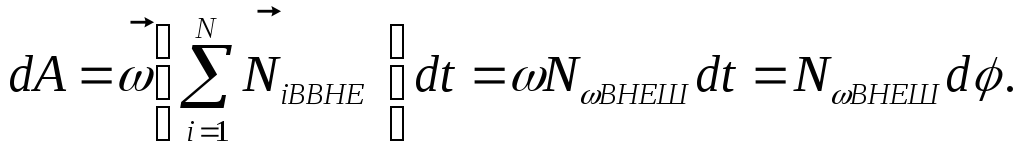
Знак
работы зависит от знака
![]() ,
т.е. от знака проекции вектора момента
силы на ось вращения.
,
т.е. от знака проекции вектора момента
силы на ось вращения.
Эта работа идет
на приращение кинетической энергии,
поэтому
![]() .
.
5.7. Кинетическая энергия при плоском движении
Плоское движение может быть представлено как наложение двух движений
– поступательного
со скоростью центра масс
![]()
- вращательного
вокруг некоторой оси с угловой скоростью
![]() .
.
Скорость
![]() -той
элементарной массы равна
-той
элементарной массы равна![]() ,
,
где
![]() -радиус-вектор элементарной массы,
проведенный из оси вращения.
-радиус-вектор элементарной массы,
проведенный из оси вращения.
Кинетическая
энергия
![]() -той
массы равна
-той
массы равна
![]() .
(5.8)
.
(5.8)
Ясно, что
![]() ,
где
,
где![]() - расстояние от массы
- расстояние от массы
![]() до оси вращения,
до оси вращения,
Тогда
![]() и
и![]() .
.
Просуммировав выражение (5.8) по всем точкам, имеем
![]() .
.
Здесь
![]() -радиус-вектор центра масс, проведенный
из оси вращения,
-радиус-вектор центра масс, проведенный
из оси вращения,
![]() -
момент инерции тела.
-
момент инерции тела.
Тогда
![]() .
.
Если ось вращения
проходит через центр масс,
![]() и
и![]() ,
(5.9)
,
(5.9)
где
![]() -момент инерции тела относительно
оси, проходящей через центр масс.
-момент инерции тела относительно
оси, проходящей через центр масс.
5.8. Условия равновесия твердого тела
Тело может оставаться в состоянии покоя в том случае, когда нет причин, приводящий к возникновения поступательного движения или вращения.
Для этого необходимо выполнение двух условий:
сумма всех сил, приложенных к телу, должна быть равна нулю:
 ,
(5.10)
,
(5.10)результирующий момент всех внешних сил относительно любой неподвижной оси
 должен
быть равен нулю:
должен
быть равен нулю: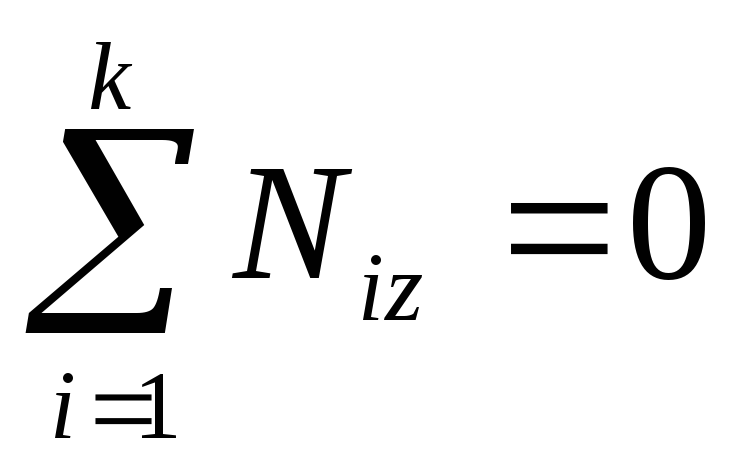 .
(5.11)
.
(5.11)
Практически оказывается достаточным, чтобы условие (5.11) выполнялось для трех любых неподвижных осей, не лежащих в одной плоскости. Тогда оно будет выполняться для любой оси.
Соотношения (5.10) и (5.11) являются условиями равновесия твердого тела.
