5.4. Момент инерции

• Согласно формуле (5.2), момент инерции тела – аддитивная величина

,

момент инерции тела равен сумме моментов инерции всех его частиц.

• Момент инерции существует безотносительно к вращению. Каждое тело, независимо от того, вращается оно или нет, обладает определенным моментом инерции относительно любой оси.

• Из выражения (5.7) следует, что один и тот же момент силы вызывает большее угловое ускорение у того тела, у которого момент инерции меньше. Таким образом,момент инерции является мерой инертности тела при вращательном движении.

Эту формулу можно представить в виде ,

где -плотность -той частицы,-ее объем.

Если тело однородно, его плотность постоянна, и суммирование по всем частицам сводится к интегралу: Интегрирование производится по всему объему тела. Величиныизависят от местоположения частицы, т.е. являются функциями ее координат.

пример:Найдем момент инерции однородного диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр (рис. 5.12).

• Разобьем диск на кольцевые слои толщинойирассмотрим один такой слой.

• все его точки находятся на одинаковом расстоянии от оси вращения, равном . Объем слоя равен,

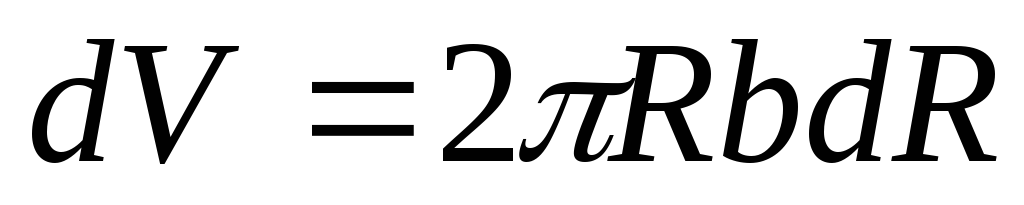где -толщина диска.

• диск однородный, его плотность одинакова во всех точках, тогда момент инерции диска равен

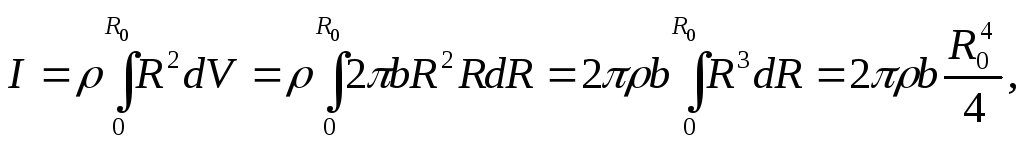
где -радиус диска.

• масса диска равна ,

• получаем .

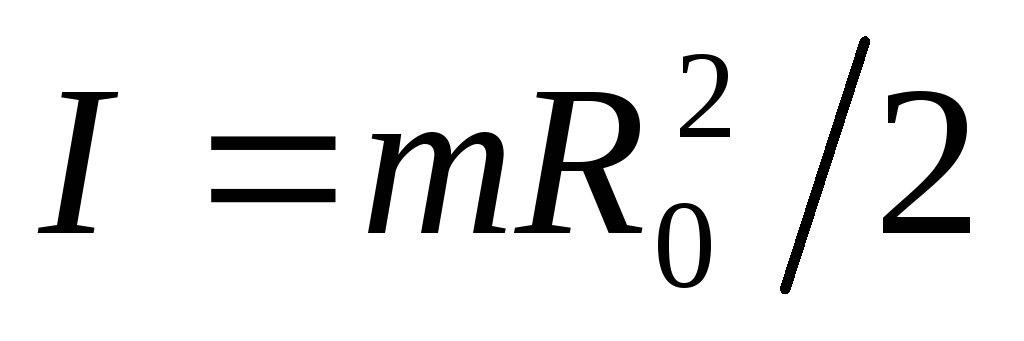Определение момента инерции тела относительно произвольной оси существенно упрощается, если воспользоваться теоремой Штейнера:момент инерции относительно произвольной оси равен сумме момента инерцииотносительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояниямежду осями.

Д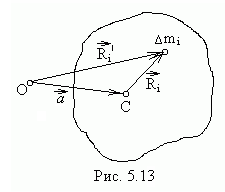оказательство теоремы.

• Рассмотрим ось С(рис.5.13), проходящую через центр масс тела, и параллельную ей осьО, отстоящую от точкиСна расстояние.

• Из точки на оси О к осиСпроведем вектор,перпендикулярный к обеим осям.

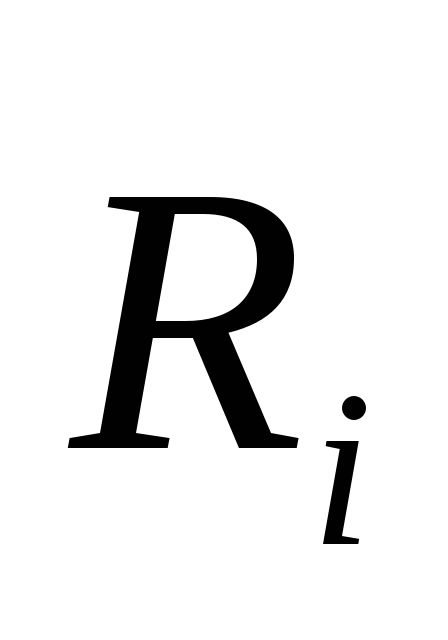• Из конца вектора проведем вектор, перпендикулярный к осиСв точку с элементарной массой.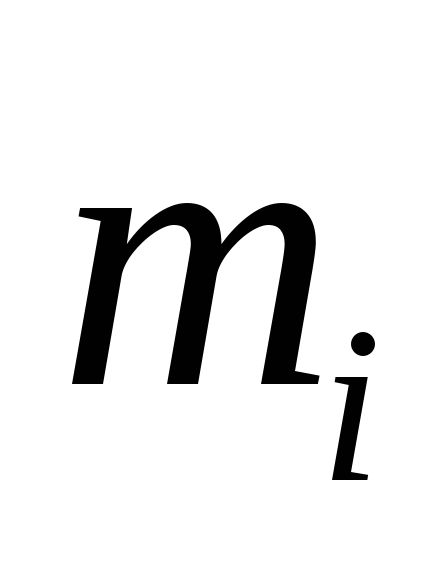

• Аналогичный вектор 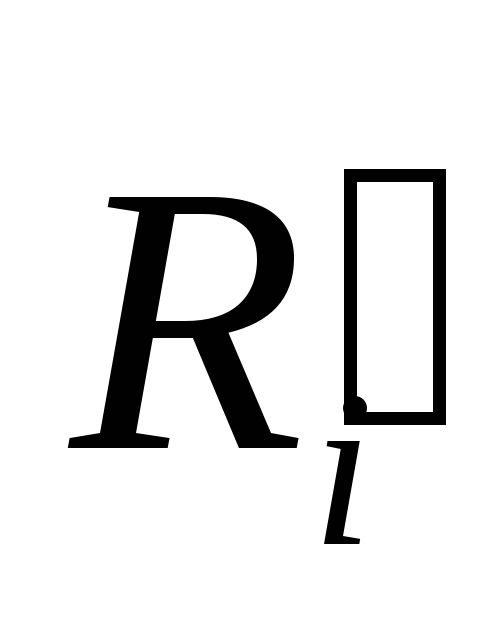проведем из начала векторак той же элементарной массе.

• Из рисунка видно, что

• Квадрат расстояния от оси С до выбранной частицы равен , а от осиО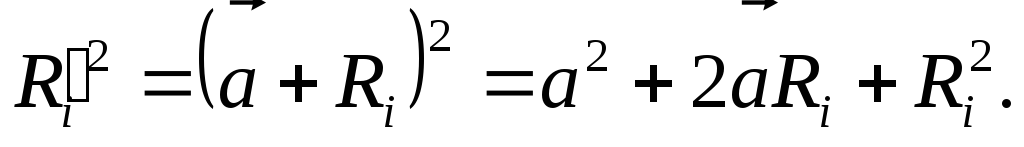

• Тогда момент инерции относительно оси О

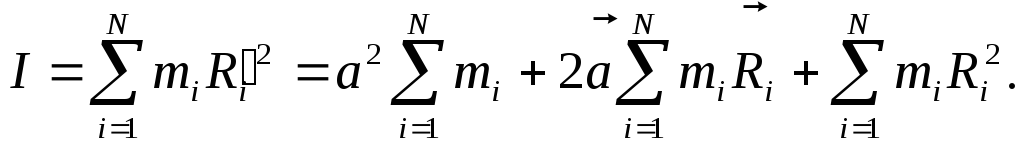где

- момент инерции тела относительно оси С,

- масса тела,

, где -вектор, проведенный от оси С к центру масс тела,=0, так как центр масс лежит на осиС, поэтому второе слагаемое равно нулю.

• Тогда получаем

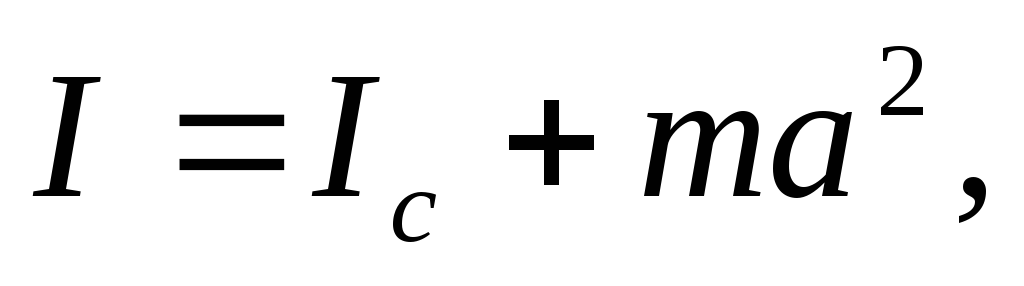
что и требовалось доказать.

В случае произвольного твердого теласвязь между векторами иболее сложная, чем рассмотренная выше. Однако модули этих векторов всегда остаются пропорциональны друг другу, следовательно, каждая компонента векторабудет линейно зависеть от компонент вектора:

Здесь и т.д. –коэффициенты пропорциональности, имеющие размерность момента инерции.

При увеличении в некоторое число раз в такое же число раз увеличится каждая из компонент,,и каждая из компонент, а значит, и сам вектор. Взаимная ориентация векторовиопределяется значениями коэффициентов пропорциональности. Все сказанное означает, чтоэти коэффициенты являются компонентами тензора второго ранга, который называется тензором инерции