1.8. Применение теоремы Гаусса к расчету полей

Найдем напряженность электрического поля

1. бесконечной нити, заряженной с линейной плотностью заряда (рис.1).

Построим гауссову поверхность в виде цилиндра, ось которого совпадает с нитью

Радиус цилиндра r, высота h .

В силу симметрии рассматриваемого поля линии вектора напряженности расходятся радиально от нити, ипоток вектора отличен от нуля только через боковую поверхность цилиндра:

Очевидно, на одинаковом расстоянии r от нити значения Е будут одинаковы, поэтому

Согласно теореме Гаусса

где -заряд, заключенный внутри гауссова цилиндра.

Тогда

и -напряженность поля заряженной нити на расстоянии r от нее.

2. бесконечной однородной заряженной плоскости.

Поверхностная плотность заряда во всех точках плоскости одинакова .

Напряженность поля перпендикулярна к плоскости.

В симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна понаправлению.

Выделим цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и основаниями .

В силу симметрии .

Поток через боковую поверхность равен нулю, так как ,

таким образом суммарный поток через поверхность цилиндра равен ,и

3. созданноедвумя разноименно заряженными плоскостями

с поверхностными плотностями заряда и.

Очевидно,

напряженности полей плоскостей направлены в одну сторону (от положительной плоскости к отрицательной, рис.3),

и результирующая напряженность ,

где - напряженность поля одной заряженной плоскости.

Окончательно получаем

4. создаваемого заряженной сферой радиуса R.

Заряд сферы q, его поверхностная плотность

Для определения напряженности построим гауссову поверхность в виде сферы радиуса r, центр которой совпадает с центром заряженной сферы.

• При r≤R внутри гауссовой поверхности зарядов нет, так как весь заряд распределен по поверхности сферы.

По теореме Гаусса или,

следовательно, -напряженность электрического поля внутри заряженной сферы равна нулю.

• При внутрь гауссовой поверхности попадает весь заряд q сферы.

В силу центральной симметрии поля напряженность на расстоянии r от центра сферы всюду одинакова, и

или

при этом ,

тогда ,

и

С ростом r значения Е убывают пропорционально (рис.6).

На поверхности сферы напряженность испытывает скачек

5. созданное объемно заряженным шаром радиуса R .

Объемная плотность заряда шара ρ.

Гауссову поверхность построим в виде сферы, центр которой совпадает с центром шара, а радиус равен r (рис.7).

• При внутрь гауссовой поверхности попадает заряд ,

тогда по теореме Гаусса , и.

На поверхности шара при r=R напряженность .

• При внутрь гауссовой поверхности попадает весь заряд 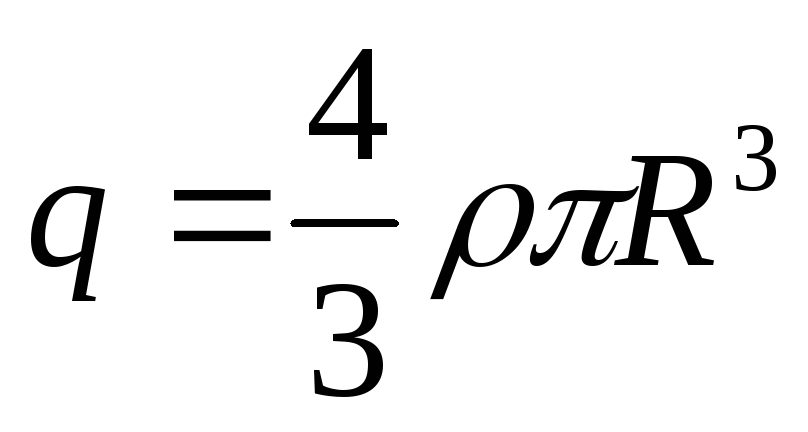, и, отсюда

• На поверхности сферы т.е.и скачка напряженности не происходит.

• Зависимость 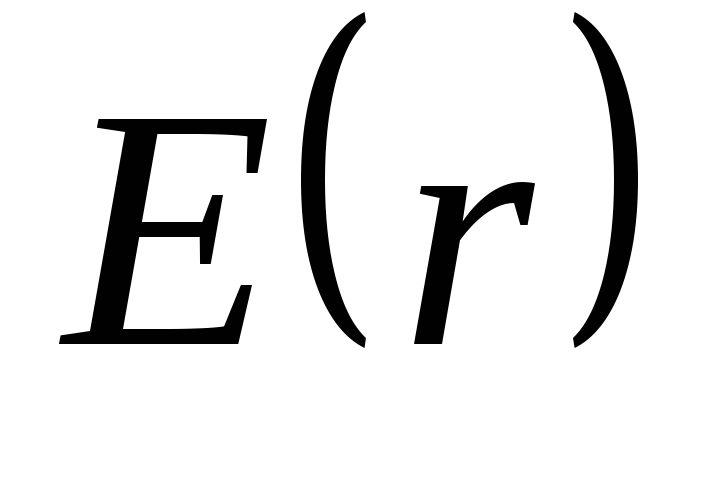представлена на рис.7.

20