1.2. Закон Кулона

Основной закон взаимодействия электрических зарядов был найден Шарлем Кулоном в 1785 г. экспериментально. Кулон установил, что сила взаимодействия между двумя небольшими заряженными металлическими шариками обратно пропорциональна квадрату расстояниямежду ними и зависит от величины зарядови:

,

где -коэффициент пропорциональности .

Силы, действующие на заряды, являются центральными, то есть они направлены вдоль прямой, соединяющей заряды.

• Для одноименных зарядов произведение 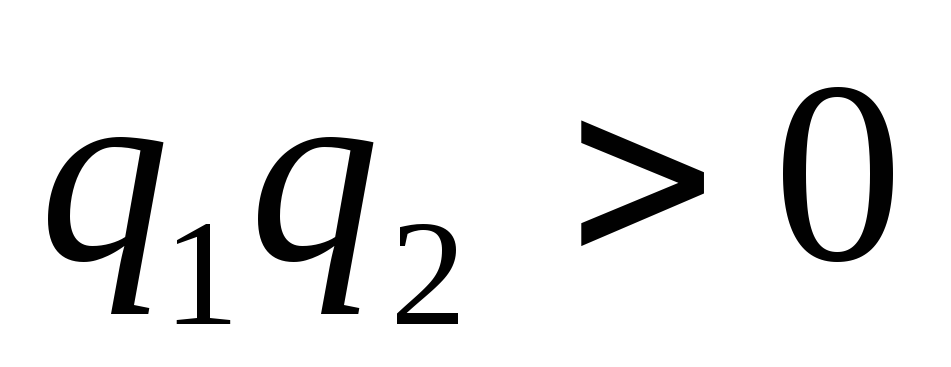и силасоответствует взаимному отталкиванию зарядов,

• для разноимнных зарядов , и силасоответствует взаимному притяжению зарядов.

Закон Кулона можно записать в векторной форме:,

где -вектор силы, действующей на заряд со стороны заряда,

- радиус-вектор, соединяющий заряд с зарядом;

- модуль радиус-вектора.

Сила, действующая на заряд со стороныравна,.

Закон Кулона в такой форме

• справедлив только для взаимодействия точечных электрических зарядов, то есть таких заряженных тел, линейными размерами которых можно пренебречь по сравнению с расстоянием между ними.

• выражает силу взаимодействия между неподвижными электрическими зарядами, то есть это электростатический закон.

Формулировка закона Кулона:

Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними.

Коэффициент пропорциональности в законе Кулоназависит

1. от свойств среды

2. выбора единиц измерения величин, входящих в формулу.

Поэтому можно представить отношением,

где -коэффициент, зависящий только от выбора системы единиц измерения;

- безразмерная величина, характеризующая электрические свойства среды, называется относительной диэлектрической проницаемостью среды. Она не зависит от выбора системы единиц измерения и равна единице в вакууме.

Тогда закон Кулона примет вид:,

для вакуума ,

тогда -относительная диэлектрическая проницаемость среды показывает, во сколько раз в данной среде сила взаимодействия между двумя точечными электрическими зарядами и, находящимися друг от друга на расстоянии, меньше, чем в вакууме.

В системе СИ коэффициент , и

закон Кулона имеет вид:.

Это рационализированная запись закона Кулона.

- электрическая постоянная, .

В системе СГСЭ ,.

В векторной форме закон Кулона принимает вид

где -вектор силы, действующей на заряд со стороны заряда ,

- радиус-вектор, соединяющий заряд с зарядом

(рис. 1.2),

r –модуль радиус-вектора .

Всякое заряженное тело состоит из множества точечных электрических зарядов, поэтому электростатическая сила, с которой одно заряженное тело действует на другое, равна векторной сумме сил, приложенных ко всем точечным зарядам второго тела со стороны каждого точечного заряда первого тела.

1.3.Электрическое поле. Напряженность.

Пространство, в котором находится электрический заряд, обладает определенными физическими свойствами.

1. На всякий другой заряд, внесенный в это пространство, действуют электростатические силы Кулона.

2. Если в каждой точке пространства действует сила, то говорят, что в этом пространстве существует силовое поле.

3. Поле наряду с веществом является формой материи.

4. Если поле стационарно, то есть не меняется во времени, и создается неподвижными электрическими зарядами, то такое поле называется электростатическим.

Электростатика изучает только электростатические поля и взаимодействия неподвижных зарядов.

Для характеристики электрического поля вводят понятие напряженности. Напряженностью в каждой точке электрического поля называется вектор , численно равный отношению силы, с которой это поле действует на пробный положительный заряд, помещенный в данную точку, и величины этого заряда, и направленный в сторону действия силы.

Пробный заряд, который вносится в поле, предполагается точечным и часто называется пробным зарядом.

- Он не участвует в создании поля, которое с его помощью измеряется.

- предполагается, что этот заряд не искажает исследуемого поля, то есть он достаточно мал и не вызывает перераспределения зарядов, создающих поле.

Если на пробный точечный заряд поле действует силой, то напряженность.

Единицы напряженности:

СИ:

СГСЭ:

В системе СИ выражение для поля точечного заряда:

.

В векторной форме:

Здесь – радиус-вектор, проведенный из зарядаq , создающего поле, в данную точку.

Т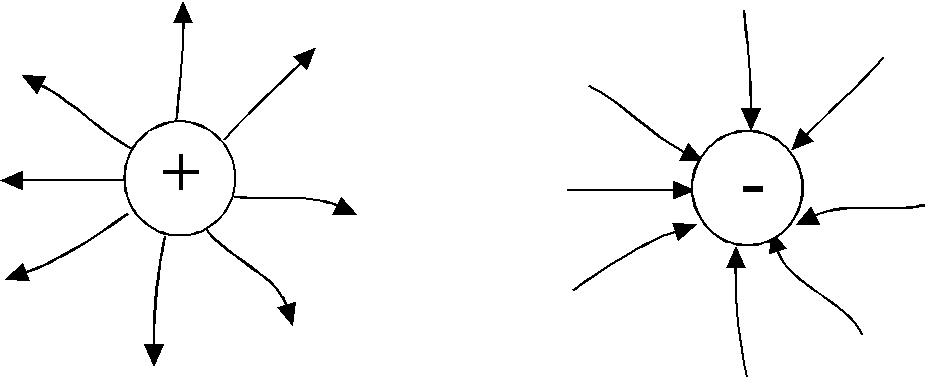аким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3)

- от заряда, если он положительный, «исток»

- и к заряду, если он отрицательный «сток»

Для графической интерпретации электрического поля вводят понятие силовой линии или линии напряженности. Это

• кривая, касательная в каждой точке к которой совпадает с вектором напряженности.

• Линия напряженности начинается на положительном заряде и заканчивается на отрицательном.

• Линии напряженности не пересекаются, так как в каждой точке поля вектор напряженности имеет лишь одно направление.