
- •7.Элементы механики сплошных сред
- •7.2. Давление в текущей жидкости. Уравнение Бернулли и следствие из него
- •7.3.Истечение жидкости из отверстия
- •7.4 . Вязкая жидкость. Силы внутреннего трения
- •7.6. Ламинарное и турбулентное движение. Число Рейнольдса
- •7.7. Течение жидкости в круглой трубе
- •7.8. Движение тел в жидкостях и газах. Лобовое сопротивление при обтекании тел
- •7.9. Идеально упругое тело. Упругие напряжения и деформации. Закон Гука. Модуль Юнга. Энергия упругих деформаций твердого тела
7.4 . Вязкая жидкость. Силы внутреннего трения
И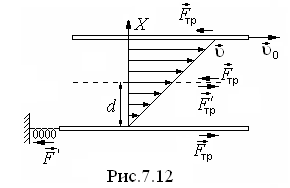 деальная
жидкость, т.е. жидкость без трения,
является абстракцией. Всем реальным
жидкостям и газам в большей или меньшей
степени присуща вязкость или внутреннее
трение.
деальная
жидкость, т.е. жидкость без трения,
является абстракцией. Всем реальным
жидкостям и газам в большей или меньшей
степени присуща вязкость или внутреннее
трение.
Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия сил, его вызвавших, постепенно прекращается.
. Рассмотрим две параллельные друг другу пластины, помещенные в жидкость (рис.7.12). Линейные размеры пластин много больше расстояния между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней с некоторой
скоростью![]() .
Экспериментально доказано, что для
перемещения верхней пластины с постоянной
скоростью
.
Экспериментально доказано, что для
перемещения верхней пластины с постоянной
скоростью![]() необходимо воздействовать на нее вполне
определенной постоянной по величине
силой
необходимо воздействовать на нее вполне
определенной постоянной по величине
силой![]() .
Пластина не получает ускорения,
следовательно, действие этой силы
уравновешивается равной ей по величине
силой, которая и есть сила трения,
действующая на пластину при ее движении
в жидкости. Обозначим ее
.
Пластина не получает ускорения,
следовательно, действие этой силы
уравновешивается равной ей по величине
силой, которая и есть сила трения,
действующая на пластину при ее движении
в жидкости. Обозначим ее![]() .
Из опыта известно, что
.
Из опыта известно, что
 (7.4)
(7.4)
где
![]() -коэффициент вязкости жидкости.
-коэффициент вязкости жидкости.
Нижняя
пластина при движении верхней также
оказывается подверженной действию
силы
![]() ,
равной по величине
,
равной по величине![]() .
Для того, чтобы нижняя пластина оставалась
неподвижной, силу
.
Для того, чтобы нижняя пластина оставалась
неподвижной, силу![]() необходимо уравновесить силой
необходимо уравновесить силой![]() .
.
Таким
образом, при движении двух погруженных
в жидкость пластин друг относительно
друга между ними возникает взаимодействие,
характеризуемое силой (7.4).Воздействие
пластин друг на друга осуществляется
через жидкость, заключенную между
пластинами, передаваясь от одного слоя
жидкости к другому. Если в любом месте
зазора провести плоскость, параллельную
пластинам, то часть жидкости, лежащей
над этой плоскостью, действует на часть
жидкости, лежащей под плоскостью, с
силой
![]() ,
а часть жидкости, лежащей под плоскостью,
действует на часть жидкости, лежащей
над плоскостью, с силой
,
а часть жидкости, лежащей под плоскостью,
действует на часть жидкости, лежащей
над плоскостью, с силой![]() .
При этом
.
При этом![]() и
и![]() определяются формулой (7.4). Таким образом,
эта формула выражает силу между
соприкасающимися слоями жидкости.
определяются формулой (7.4). Таким образом,
эта формула выражает силу между
соприкасающимися слоями жидкости.
Экспериментально доказано, что скорость частиц жидкости изменяется в направлении z, перпендикулярном пластинам (рис.7.6) по линейному закону
![]() .
(7.5)
.
(7.5)
Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорость, как и сами пластины. Из формулы (7.5) получаем
![]()
Знак
модуля в этой формуле поставлен по
следующей причине. При изменении
направления движения производная
скорости изменит знак, в то время как
отношение
![]() всегда положительно. С учетом сказанного
выражение (7.4) принимает вид
всегда положительно. С учетом сказанного
выражение (7.4) принимает вид
![]() .
(7.6)
.
(7.6)
Единицей
вязкости с СИ служит такая вязкость,
при которой градиент скорости с модулем
![]() ,
приводит к возникновению силы внутреннего
трения в 1 Н на 1м
,
приводит к возникновению силы внутреннего
трения в 1 Н на 1м![]() поверхности касания слоев. Эта единица
называется Паскаль - секундой (Па ·с ).
поверхности касания слоев. Эта единица
называется Паскаль - секундой (Па ·с ).
