7.2. Давление в текущей жидкости. Уравнение Бернулли и следствие из него

Рассматривая движение жидкостей, в ряде случаев можно считать, что перемещение одних жидкостей относительно других не связано с возникновением сил трения. Жидкость, которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной.

Выделим в стационарно текущей идеальной жидкости трубку тока малого сечения (рис.7.10). Рассмотрим объем жидкости, ограниченный стенками трубки тока и перпендикулярными к линиям тока сечениями и.За времяэтот объем переместиться вдоль трубки тока, причем сечениепереместиться в положение,пройдя путь, сечениепереместиться в положение , пройдя путь .В силу неразрывности струи заштрихованные объемы будут иметь одинаковую величину :

Энергия каждой частицы жидкости равна сумме ее кинетической энергии и потенциальной в поле силы тяжести. Вследствие стационарности течения частица, находящаяся спустя время в любой из точек незаштрихованной части рассматриваемого объема (например точкаO на рис. 7.10 ), имеет такую же скорость (и такую же кинетическую энергию), какую имела частица, находившаяся в той же точке в начальный момент времени. Поэтому приращение энергии всего рассматриваемого объема равно разности энергий заштрихованных объемови.

Будем считать, что сечение трубки тока и отрезки настолько малы, что все точки каждого из заштрихованных объемов имеют одинаковые значения скорости, давленияи высотыh. Тогда приращение энергии

. (7.1)

В идеальной жидкости силы трения отсутствуют, поэтому приращение энергии (7.1) равно работе, совершаемой над выделенным объемом силами давления. Силы давления на боковую поверхность перпендикулярны в каждой точке к направлению перемещения частиц и работы не совершают. Работа сил, приложенных к сечениямиравна

. (7.2)

Приравняв (7.1) и (7.2), получаем

. (7.3)

Так как сечения ибыли взяты произвольно, то можно утверждать, что выражениеостается постоянным в любом сечении трубки тока, т.е. в стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие

.

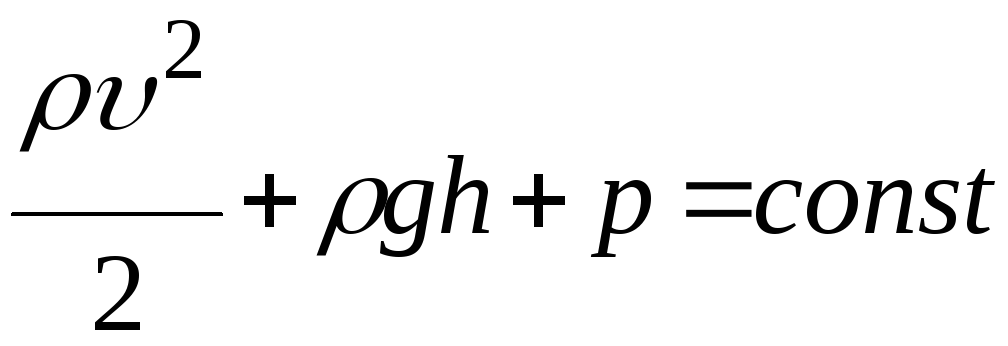Это уравнение Бернулли. Для горизонтальной линии тока уравнение (7.3) принимает вид:

7.3.Истечение жидкости из отверстия

Применим уравнение Бернулли к случаю истечения жидкости из малого отверстия в широком открытом сосуде. Выделим в жидкости трубку тока, верхнее сечение которой лежит на поверхности жидкости, а нижнее совпадает с отверстием (рис.7.11). В каждом их этих сечений скорость и высоту над некоторым исходным уровнем можно считать одинаковыми, давления в обоих сечениях равны атмосферному и также одинаковы, скорость перемещения открытой поверхности будем считать равной нулю. Тогда уравнение (7.3) принимает вид:

где - скорость истечения жидкости из отверстия. Обозначим, сократим на, тогда

.

Это формула Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, расположенного на глубине под открытой поверхностью, совпадает со скоростью, которую приобретает тело, падая с высотыh.

Струя жидкости, вытекающая из отверстия в сосуде (рис.7.11) уносит с собой за время импульс(здесь-плотность жидкости,S-площадь отверстия, -скорость истечения струи). Этот импульс сообщается вытекающей жидкости сосудом. По третьему закону Ньютона сосуд получает от вытекающей жидкости за времяимпульс, т.е. испытывает действие силы

.

Эта сила называется реакцией вытекающей струи. Если сосуд поставить на тележку, то он придет в движение в направлении, противоположном движению струи. Подставив значение скорости истечения, получаем выражение для модуля силы реакции струи

.

Если бы сила совпадала по величине с силой гидростатического давления, которое оказывала бы жидкость на пробку, закрывающую отверстие, тобыла бы равна. На самом делеоказывается в два раза большей. Это связано с тем. Что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем вблизи стенки, лежащей против отверстия, давление оказывается несколько большим, чем вблизи стенки в которой сделано отверстие.