
- •Ш. А. Пиралишвили, н. А. Мочалова, с. В. Веретенников термодинамика. Технические приложения
- •Рыбинск 2007
- •1.1. Способы задания газовой смеси
- •1.4. Энтропия газовой смеси
- •1.5. Задание для самостоятельного решения
- •1.6. Пример выполнения индивидуального задания
- •2. Процессы смешения
- •2.1. Процессы смешения в постоянном объеме
- •2.2. Задание для самостоятельной проработки
- •2.3. Пример выполнения расчета
- •2.4. Смешение в потоке
- •2.5. Индивидуальные задания по расчету
- •2.6. Пример выполнения индивидуального задания
- •2.7. Смешение при заполнении объема
- •2.8. Индивидуальное задание на расчет процесса смешения при заполнении объема
- •2.9. Пример выполнения индивидуального задания по расчету процесса смешения при заполнении объема
1.6. Пример выполнения индивидуального задания
Дано:
1. Смесь задана следующим объемным составом.
![]() %;
%;
![]() %;
%;![]() %,
%,
или в объемных долях
![]() ;
;
![]() ;
;
![]() .
.
2. Температура, при
которой определяется истинная теплоемкость
смеси,
![]() С
(2273 К).
С
(2273 К).
3. Интервал температур, для которого определяется средняя теплоемкость смеси:
![]() С
(
С
(![]() К);
К);
![]() С
(
С
(![]() К).
К).
Решение.
1. В исходных данных смесь газов задана объемными долями. Воспользовавшись формулой раздела 1.2 определим через массовые доли состав смеси
![]() .
.
Запишем молярные массы компонентов:
![]() кг/моль;
кг/моль;
![]() кг/моль;
кг/моль;
![]() кг/моль;
кг/моль;
![]() кг/моль;
кг/моль;
Тогда массовая доля углекислого газа:
![]() .
.
Аналогично находим массовые доли остальных компонентов:
![]() ;
;
![]() ;
;![]() .
.
Сумма массовых долей:
![]() .
.
2. Газовые постоянные компонентов определяем по формуле:
![]() ,
Дж/(кг·К);
,
Дж/(кг·К);
![]()
![]()
![]() ;
;
![]()
3. Газовую постоянную смеси находим по формуле (1.16) раздела 1.2:
![]() ;
;
![]() Дж/(кг·К).
Дж/(кг·К).
4. Найдем значение кажущейся молекулярной массы смеси, заданной объемными долями, формуле (1.18):
![]()
![]()
![]() кг/моль.
кг/моль.
Если смесь задана
массовыми долями, то
![]()
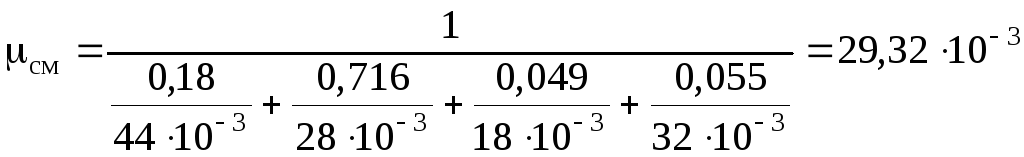 кг/моль.
кг/моль.
Сделаем проверку
полученных значений
![]() ,
учитывая, что
,
учитывая, что
![]()
![]() кг/моль.
кг/моль.
5. Найдем парциальные давления компонентов через объемные доли:
![]()
![]() (Па)
= 12 (кПа);
(Па)
= 12 (кПа);
![]() (кПа);
(кПа);
![]() (кПа);
(кПа);
![]() (кПа).
(кПа).
Парциальные
давления компонентов, выраженные через
массовые доли:
![]()
![]() (кПа);
(кПа);
![]() (кПа);
(кПа);
![]() (кПа);
(кПа);
![]() (кПа).
(кПа).
Сделаем проверку:
![]() ;
;
![]()
![]()
6. Найдем массу
смеси:
![]()
![]() (кг).
(кг).
7. Определим массовые доли компонентов через массовые доли:
![]()
![]() (кг);
(кг);
![]() (кг);
(кг);
![]() (кг);
(кг);
![]() (кг).
(кг).
Сделаем проверку:
![]()
![]() .
.
8. Рассчитаем парциальные объемы компонентов через объемные доли:
![]() (при
(при
![]() и
и![]() ):
):
![]() (м3);
(м3);
![]() (м3);
(м3);
![]() (м3);
(м3);
![]() (м3).
(м3).
Сделаем проверку:
![]() ;
;
![]() ;
;
![]() .
.
9. Вычислим парциальную плотность компонентов:
![]() (при
(при
![]() и
и![]() ):
):
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3).
(кг/м3).
10. Найдем плотности
компонентов при заданных условиях (при
![]() и
и![]() ):
):![]() ;
;
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3).
(кг/м3).
11. Плотность газовой
смеси при заданных условиях (при
![]() и
и![]() ):
):
– через объемные доли:
![]() ,
,
![]() (кг/м3);
(кг/м3);
– через массовые доли:
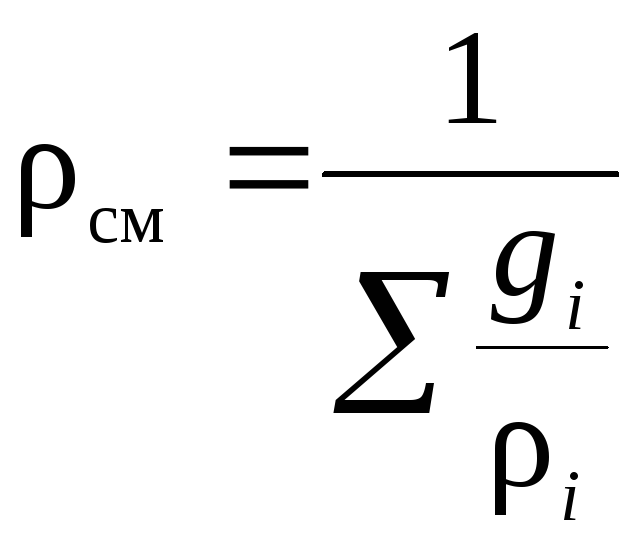 ,
,
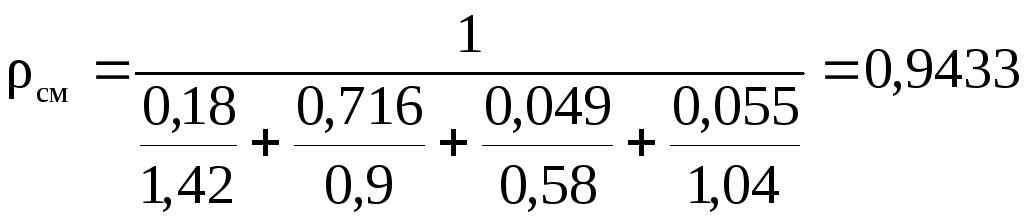 (кг/м3);
(кг/м3);
– через парциальные плотности компонентов:
![]() ;
;
![]() (кг/м3).
(кг/м3).
Сделаем проверку:
![]() (кг/м3).
(кг/м3).
12.
Найдем плотности компонентов при
нормальных физических условиях (при
![]() Па
и
Па
и
![]() К):
К):
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3);
(кг/м3);
![]() (кг/м3).
(кг/м3).
13. Найдем плотность смеси при нормальных условиях:
– через
объемные доли:
![]() ,
,
![]() (кг/м3);
(кг/м3);
– через массовые доли:
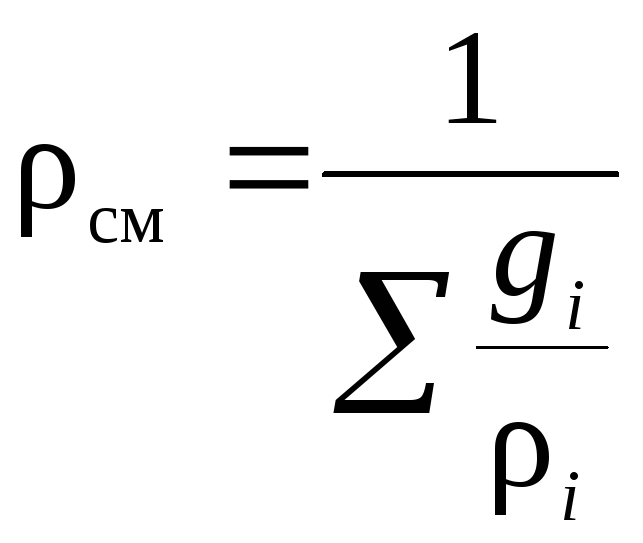 ,
,
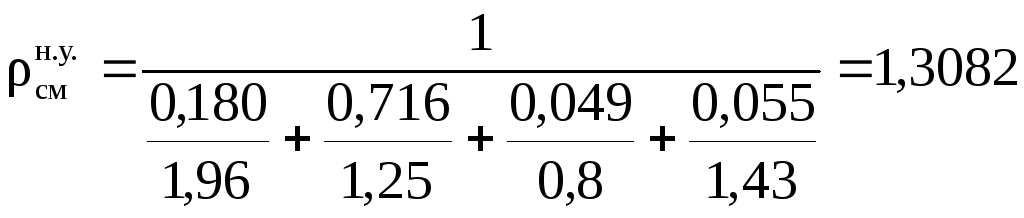 (кг/м3).
(кг/м3).
Сделаем
проверку:
![]() (кг/м3).
(кг/м3).
14.
Находим теплоемкость смеси при
![]() К:
К:
– молярную
изобарную:
![]() .
.
По
табл. 1 Приложения 2 находим молярные
изобарные теплоемкости компонентов:
![]() (Дж/(кг·К);
(Дж/(кг·К);
![]() (Дж/(кг·К);
(Дж/(кг·К);
![]() (Дж/(кг·К);
(Дж/(кг·К);
![]() (Дж/(кг·К);
(Дж/(кг·К);
![]()
![]() (Дж/кг·).
(Дж/кг·).
Молярную изохорную теплоемкость смеси найдем из уравнения Майера:
![]() ;
;
![]() Дж/(моль·К).
Дж/(моль·К).
Определим массовые теплоемкости:
![]() кДж/(кг·К);
кДж/(кг·К);
![]() кДж/(кг·К).
кДж/(кг·К).
15.
Находим среднюю теплоемкость смеси в
диапазоне изменения температур от
![]() до
до![]() по формуле:
по формуле:
![]() .
.
Значения
средних теплоемкостей
![]() выбираем по температуре
выбираем по температуре![]() из
табл. 1-5 Приложения 2.
из
табл. 1-5 Приложения 2.
– Найдем
среднюю мольную изобарную теплоемкость
смеси в интервале температур от
![]() до
до![]() :
:
![]() ,
,
где
![]() ;
;
![]()
![]()
![]() Дж/(моль·К);
Дж/(моль·К);![]()
![]() Дж/(моль·К);
Дж/(моль·К);
![]() Дж/(моль·К).
Дж/(моль·К).
Найдем среднюю мольную изохорную теплоемкость, используя уравнение Майера:
![]() ;
;
![]() Дж/(моль·К).
Дж/(моль·К).
– Величину средней объемной теплоемкости определим по известной средней мольной теплоемкости и формуле:
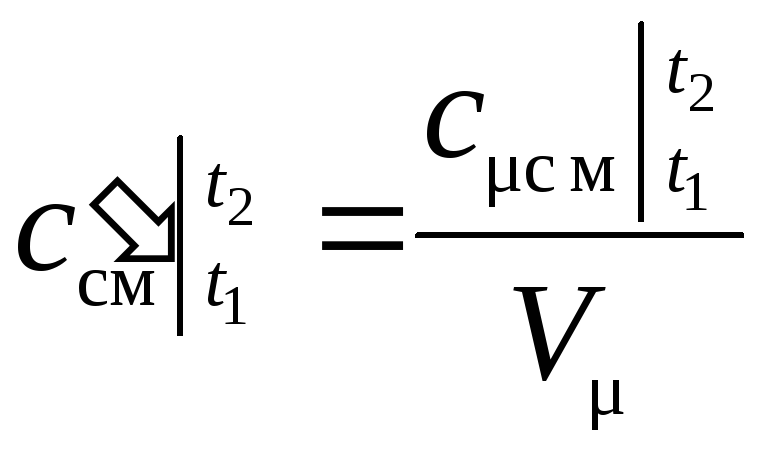 ;
;
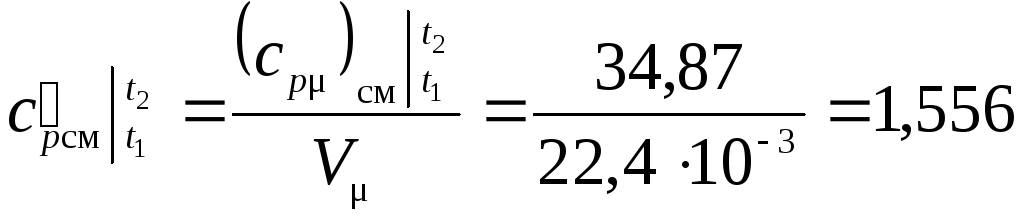 кДж/(м3·К);
кДж/(м3·К);
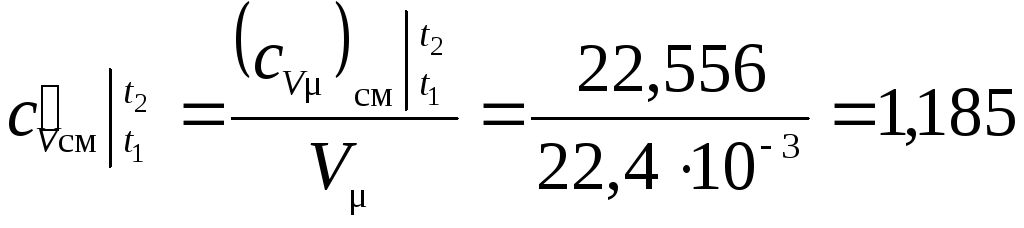 кДж/(м3·К).
кДж/(м3·К).
– Найдем значение средней массовой теплоемкости смеси:
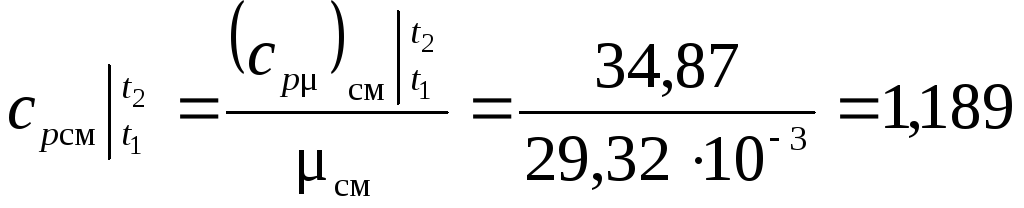 кДж/(кг·К);
кДж/(кг·К);
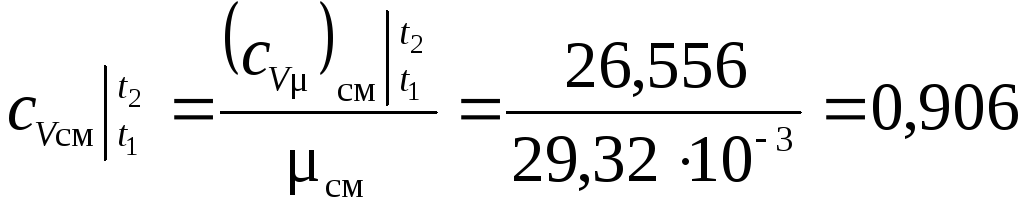 кДж/(кг·К).
кДж/(кг·К).
16.
Найдем затраты тепла на нагревание при
![]() :
:
– двух
молей смеси (![]() моль):
моль):
![]() ;
;
![]() (кДж).
(кДж).
– 10 м3
смеси (![]() м3):
м3):
![]() ;
;
![]() (кДж).
(кДж).
– 7 кг
смеси (![]() кг):
кг):
![]() ;
;
![]() (кДж).
(кДж).
