1.1. Способы задания газовой смеси

Под смесью идеальных газов понимается механическая смесь химически обособленных исходных газов, подчиняющихся уравнению состояния идеального газа. Тогда будем считать, что и смесь представляет из себя некоторый самостоятельный идеальный газ, термодинамические свойства которого определяются количественным соотношением входящих в него исходных компонентов, т. е. свойства газовой смеси однозначно определяются ее составом.

Состав газовой смеси определяется количественным соотношением входящих в него компонентов и может быть задан массовыми, объемными или мольными долями.

Пусть М_см – масса газовой смеси, а т_i – масса i-го компонента, входящего в смесь. Согласно закону сохранения массы будем иметь очевидное равенство:

, 1.1)

где n – число компонентов смеси.

Под массовой долей i-го компонента будем понимать отношение:

или в процентах %. (1.2)

На основании закона сохранения вещества, запишем уравнение баланса массы:

. (1.3)

Если массовые доли заданы в процентах, то

%. (1.4)

Объемные доли представляют собой отношение парциальных объемов компонентов к объему газовой смеси:

, (1.5)

где V_i – парциальный объем i-го компонента; V_см – объем газовой смеси.

Под парциальным объемом будем понимать тот объем, которым бы обладал i-й компонент, находясь при температуре и давлениигазовой смеси.

Нетрудно показать, что парциальные объемы газов прямо пропорциональны их парциальным давлениям. Парциальным называется давление, которое создавал бы i-й газ смеси, если бы он один занимал весь объем смеси, находясь в нем при температуре смеси. Запишем уравнение Бойля-Мариотта для компонента смеси:

, т. е. (1.6)

,

или

, ,

где P_i – парциальное давление i-го компонента; V_i – парциальный объем

i-го компонента.

Сложим почленно левые и правые части закона Бойля-Мариотта для компонентов:

или .

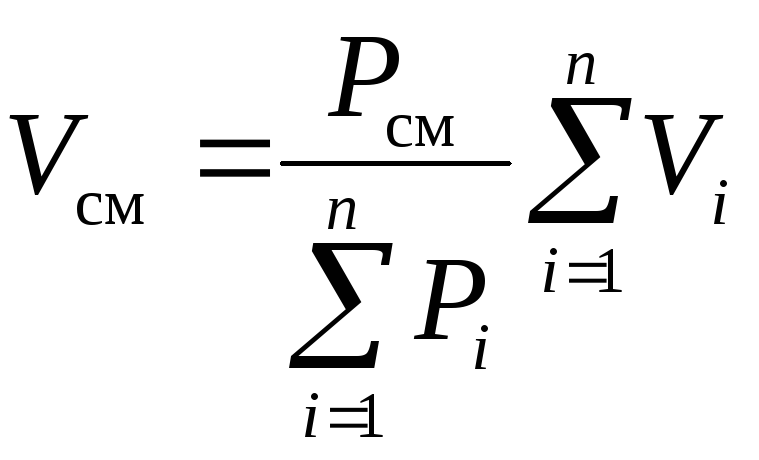Согласно закону Дальтона

, (1.7)

тогда

. (1.8)

Объем газовой смеси равен сумме парциальных объемов компонентов, входящих в смесь. Это утверждение равносильно равенству

или  %. (1.9)

Состав газовой смеси может быть задан и числом молей, входящих в нее компонентов

(1.10)

где – число молей смеси; – число молей i-го компонента.

Тогда под мольной долей будем понимать отношение

(1.11)

и, согласно закону сохранения количества вещества, будем иметь равенство

или  %. (1.12)

Воспользуемся следствием из закона Авогадро: одинаковые количества различных идеальных газов, находящихся при одинаковых давлениях и температуре, занимают одинаковые объемы.

Запишем

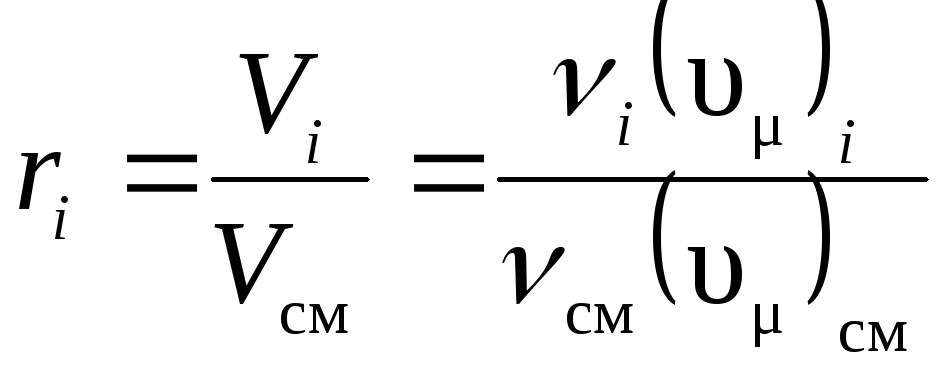, но ,

тогда

, (1.13)

т. е. объемные и мольные доли компонентов смеси равны между собой.

1.2. Термическое уравнение состояния газовой смеси

Запишем уравнение состояния для i-го компонента газовой смеси, если он занимает весь ее объем и находится там при температуре смеси. Тогда его давление равно парциальному:

. (1.14)

Просуммируем полученные зависимости для всех компонентов, входящих в смесь

.

Вспоминая, что и, вводя обозначение ,

получим уравнение состояния газовой смеси:

, (1.15)

где R_см – газовая постоянная смеси. Ее величина может быть рассчитана из соотношения

.

Поделив его на массу смеси М, получим соотношение:

, но ,

тогда

. (1.16)

Введение понятия о кажущейся молекулярной массе смеси упрощает расчеты газовых смесей:

. (1.17)

Или после подстановки выражения (1.17) для получим с учетом равенстваДж/(моль∙К)

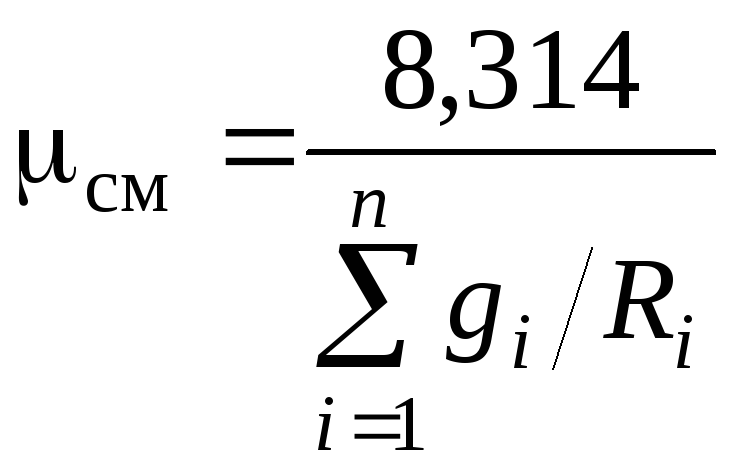. (1.18)

Запишем уравнение состояния для массы газа m_i:

или, с учетом ;

.

Последнее выражение преобразуем к виду

.

Если записать выражения для каждого компонента смеси, а затем просуммировать, получим

; ,

тогда

.

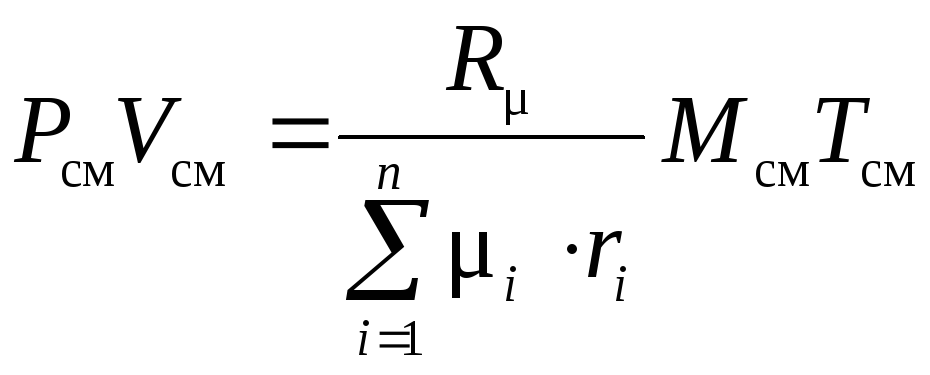Таким образом

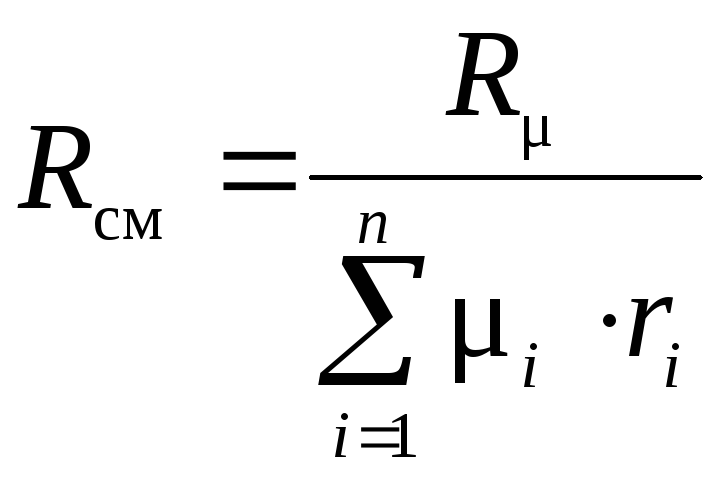, а . (1.19)

Получим расчетные зависимости для и, если смесь задана массовыми долями. Запишем уравнение состояния дляМ кг газовой смеси и для кг компонентов газов, входящих в смесь, через их парциальные объемы:

; .

Если записать второе выражение для каждого компонента, а затем их просуммировать, то получим

.

Перепишем его в виде

.

Поделив последнюю зависимость на уравнение состояния смеси для М кг, получим зависимость для расчета R_см и _см через массовый состав:

; . (1.20)

Последние выражения позволяют по объемным долям и молекулярным массам компонентов рассчитать газовую постоянную смеси и среднюю молекулярную массу.

Зная соотношения между массовыми и объемными долями газов, можно рассчитать парциальные давления

; или . (1.21)

Запишем закон Бойля-Мариотта для i-го компонента и всей смеси

,

откуда

,

тогда

или . (1.22)

Приравнивая зависимости (1.21) и (1.22), получим формулы перевода массовых долей в объемные и наоборот:

; . (1.23)

Плотность газовой смеси:

,

таким образом,

. (1.24)

Выразим через массовый состав смеси:

,

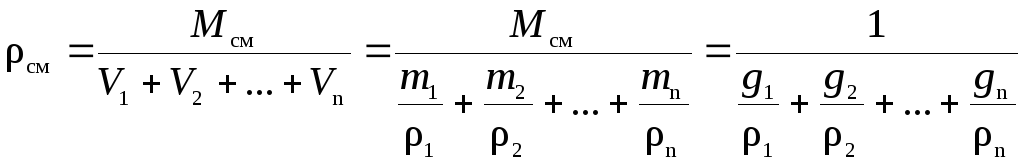следовательно, .

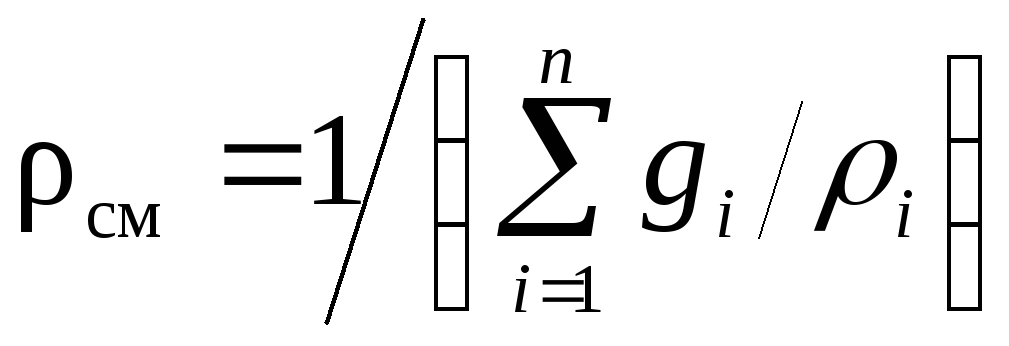1.3. Теплоемкость смеси газов

Пусть известны c_i – зависимость массовых теплоемкостей компонентов от температуры

.

Для одного килограмма газовой смеси массовая теплоемкость может быть рассчитана по формуле

. (1.25)

Или с учетом зависимости теплоемкостей от температуры

.

Если задан объемный состав, то удобней пользоваться объемными теплоемкостями:

для 1 м³ компоненты:,

для 1 м³ смеси: . (1.26)

Или с учетом зависимости от температуры:

. (1.27)