Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Рыбинский государственный авиационный технический университет им. П. А. Соловьева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1,2.doc

Скачиваний:

198

Добавлен:

08.03.2015

Размер:

6.06 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1111

2.8. Индивидуальное задание на расчет процесса смешения при заполнении объема

Типичная задача может быть сформулирована следующим образом в резервуаре содержащем м³ находится некоторый известный газ при определенном давлении и температурепо трубопроводу в него подается в течении временигаз того же (или другого) химического состава с расходомкг/с при давлениии температуре. Гидравлические потери отсутствуют. Считая газ идеальным определить параметры образовавшейся смеси, рассчитать энтропии и эксергию компонентов до смешения и газовой смеси, определить потери эксергии при смешении и построить эксергетическую диаграмму.

2.9. Пример выполнения индивидуального задания по расчету процесса смешения при заполнении объема

Условие задачи.

В резервуаре объемом 5 м³ находится кислород под давлением 300 кПа и температуре 47 °С. По трубопроводу в резервуар после открытия крана начинает поступать углекислый газ под давлением МПа и температуре°С в течении 5 с с расходом 0,12 м³/с. Считая газ идеальным, рассчитать параметры газа после смешения. Найти приращение энтропии, потери эксергии и построить эксергетическую диаграмму. Скорость течения углекислого газа 10 м/с.

Дано:

м³

Па

°С

Па

°С

м³/с

м/с

Р, Т, ,Е₁, Е₂, Е – ?

Анализ.

Задача на термодинамику идеальных газов. В процессе решения необходимо использовать уравнение Клапейрона-Менделеева, уравнения сохранения массы и энергии, первое и второе начало термодинамики, уравнение Гюи-Стодолы для расчета потерь эксергии на основании чего построить эксергетическую диаграмму процесса смешения при заполнении резервуара с кислородом, втекающим в него углекислым газом.

Решение.

Рассчитаем объем углекислого газа, поступившего в резервуар за заданный промежуток времени прокачки

м³.

Воспользуемся законом сохранения и найдем массу газовой смеси в резервуаре

Массы компонентов можно найти из уравнения Клапейрона-Менделеева в

предположении идеальности смешивающихся газов:

Тогда масса углекислого газа, поступившая в резервуар, будет равна:

кг.

Масса кислорода, содержащегося в баллоне до смешения:

кг.

Таким образом, масса газовой смеси будет равна:

кг.

Найдем массовые доли компонентов, входящих в смесь:

для кислорода

для углекислого газа

Проверим баланс по сумме массовых долей

Баланс сошелся.

Объемные доли компонентов можно найти по известным массовым долям, воспользовавшись соотношением:

Кажущуюся молекулярную массу смеси определим, воспользовавшись очевидной зависимостью:

Найдем газовые постоянные кислорода и углекислого газа:

Дж/(кг×К);

Дж/(кг×К).

После подстановки получим:

кг/моль.

Тогда объемная доля кислорода равна:

;

объемная доля углекислого газа;

Проверка .

Газовая постоянная смеси равна

Дж/(кг·К).

Найдем по таблицам Приложения 2 удельные теплоемкости для кислорода и углекислого газа:

кДж/(кг×К); кДж/(кг×К); кДж/(кг×К); кДж/(кг×К).

Запишем закон сохранения энергии для смешивающихся компонентов и газовой смеси:

или

Откуда температура полученной в резервуаре смеси будет равна:

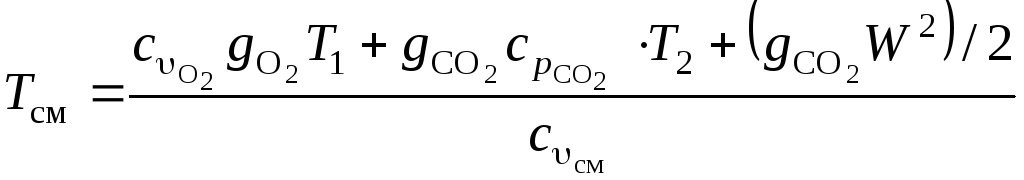Теплоемкость газовой смеси найдем по известной зависимости, полученной для расчета газовых смесей:

кДж/(кг×К).

После подстановки в предшествующую формулу, найдем результирующую температуру газовой смеси:

К.

Это значение необходимо уточнить, пересчитав теплоемкости компонентов и теплоемкость смеси, при температуре смеси и методом последовательных приближений, добиться требуемого совпадения выбора теплоемкостей как функции от температуры с рассчитанным значением температуры смеси.

Конечное давление смеси можно найти из уравнения Клапейрона-Менделеева:

Па = 0,5 МПа.

Вычислим энтропии компонентов в состоянии до смешения и энтропию газовой смеси после окончания процесса, заполнения объема.

Для расчета энтропии воспользуемся зависимостями, приведенными в первой главе пособия при расчете газовых смесей.

Энтропия газов до смешения:

кислорода:

Дж/К

углекислого газа:

Дж/К.

Энтропия системы до смешения равна сумме энтропий кислорода и углекислого газа:

Дж/К.

Удельная энтропия системы до смешения:

Дж/(кг·К).

Найдем энтропию образовавшейся газовой смеси как сумму энтропии компонентов, входящих в нее

Энтропия кислорода:

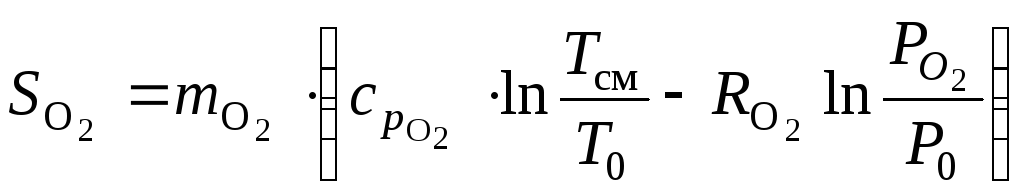Энтропия углекислого газа:

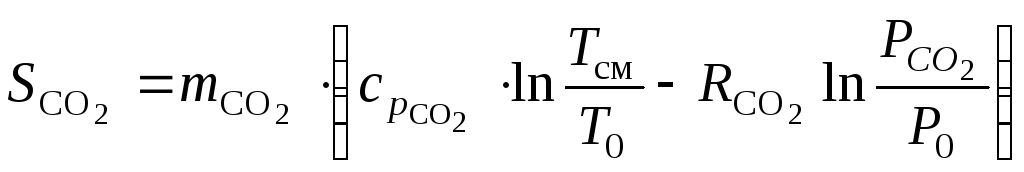Найдем парциальное давление кислорода и углекислого газа в смеси:

кПа;

кПа.

Следовательно,

Дж/К;

Дж/К.

Тогда энтропия образовавшейся газовой смеси будет равна

Дж/К.

Найдем приращение энтропии за счет необратимости процесса смешения

; Дж = 2,8 кДж.

Потери эксергии De за счет необратимости процесса смешения найдем воспользовавшись уравнением Гюи-Стодолы

кДж.

Эксергию покоящегося газа можно найти, воспользовавшись известным соотношением [4]:

где – параметры системы (газа) соответствующие состоянию окружающей среды;– начальные параметры системы.

Для потока газа эксергию 1 кг движущейся среды можно рассчитать, воспользовавшись зависимостью для потока [4]

Дальнейшее решение можно строить, предполагая газ идеальным, а энтропию при К равной нулю. В рассматриваемом примере используем таблицы термодинамических параметров газа по Ривкину [9], приведенных в Приложении настоящего пособия.