3.2 Определение погрешности расчёта

Определим погрешность выполненного расчёта. В начале определим мощность, выделяемую источником:

Вт.

Далее определим мощность, потребляемую диссипативными элементами схемы по известной формуле:

.

Подставляя численные значения найденных токов, находим:

Вт.

Погрешность определяем по известной формуле:

.

Подставляем найденные значения мощностей:

.

Как видим, точность расчёта этим методом выше точности расчёта предыдущих методов и на порядок выше точности расчёта с помощью законов Кирхгофа. Недостатком этого метода является меньшая наглядность по сравнению с другими методами.

4 Расчёт электрической цепи с помощью законов Кирхгофа

Прежде чем приступить к расчёту названным методом, рассмотрим основные положения этого метода и последовательность расчёта этим методом в соответствии .

При расчете этим методом первоначально определяются токи в ветвях, а затем напряжения на всех элементах. Токи находятся из уравнений, полученных с помощью законов Кирхгофа. Так как в каждой ветви цепи протекает свой ток, то число исходных уравнений должно равняться числу ветвей цепи. Число ветвей принято обозначать через n. Часть этих уравнений записываются по первому закону Кирхгофа, а часть - по второму закону Кирхгофа. Все полученные уравнения должны быть независимыми. Это значит, чтобы не было таких уравнений, которые могут быть получены путем перестановок членов в уже имеющемся уравнении или путем арифметических действий между исходными уравнениями. При составлении уравнений используются понятия независимых и зависимых узлов и контуров.

Независимым узлом называется узел, в который входит хотя бы одна ветвь, не входящая в другие узлы. Если число узлов обозначим через К, то число независимых узлов равно (К-1).

Независимым контуром называется контур, который отличается от других контуров хотя бы одной ветвью, не входящей в другие контура. В противном случае такой контур называется зависимым.

Если число ветвей цепи равно n, то число независимых контуров равно

[n-(К-1)].

4.1 Последовательность расчёта

1. Расставляем условно – положительные направления токов и напряжений.

2. Определяем число неизвестных токов, которое равно числу ветвей (n).

3. Определяем число независимых узлов и контуров и выбираем их на схеме.

4. С помощью первого закона Кирхгофа составляем (К–1) уравнений для независимых узлов.

5. С помощью второго закона Кирхгофа составляем [n – (К–1)] уравнений для независимых контуров. При этом напряжения на элементах выражаются через токи, протекающие через них.

6. Решаем составленную систему уравнений и определяем токи в ветвях. При получении отрицательных значений для некоторых токов, необходимо их направления в схеме изменить на противоположные, которые и являются истинными.

7. Определяем падения напряжений на всех элементах схемы.

В соответствии с рассмотренной последовательностью расчёта, расставляем на схеме условно-положительные направления токов и напряжений. Это уже было сделано и показано на рис.3.

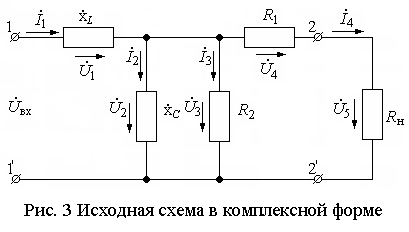
На схеме имеют место две ветви, содержащие Xc и R2 которые включены параллельно и, как бывает у параллельно соединённых ветвей, у них должны быть общие узлы с обеих сторон соединения. Однако на схеме каждая ветвь имеет свой узел, между которыми находится перемычка. Такие узлы принято называть распределёнными и на схеме они воспринимаются как один узел. В схеме в этих случаях токи в перемычках не представляют интереса и их не определяют. Исходя из сказанного, в схеме имеется четыре ветви, а значит в схеме четыре неизвестных тока.

С учётом сказанного, в схеме только два узла, а в качестве независимого узла выберем верхний распределённый узел и для него, в дальнейшем будет записано уравнение по первому закону Кирхгофа.

В схеме три независимых контура. Выбираем контура, содержащие такие элементы: ,. Для каждого контура составляются уравнения по второму закону Кирхгофа.

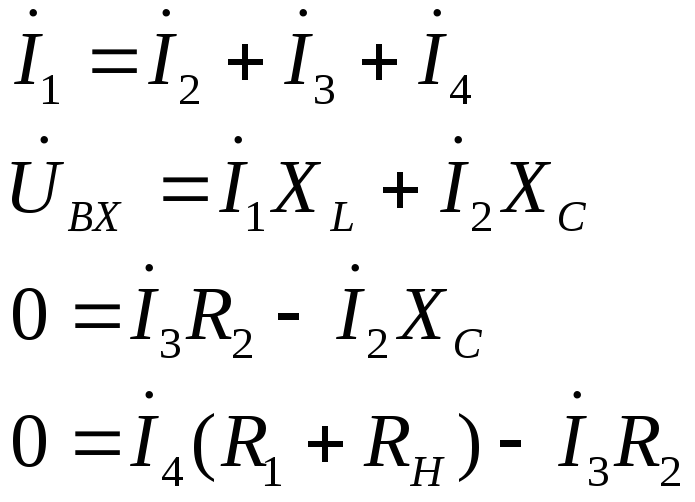
Расчёт системы можно проводить методом Крамара или методом последовательного исключения. Воспользуемся методом последовательного исключения. Подставим первое уравнение системы во второе уравнение. После эквивалентного преобразования система принимает вид :

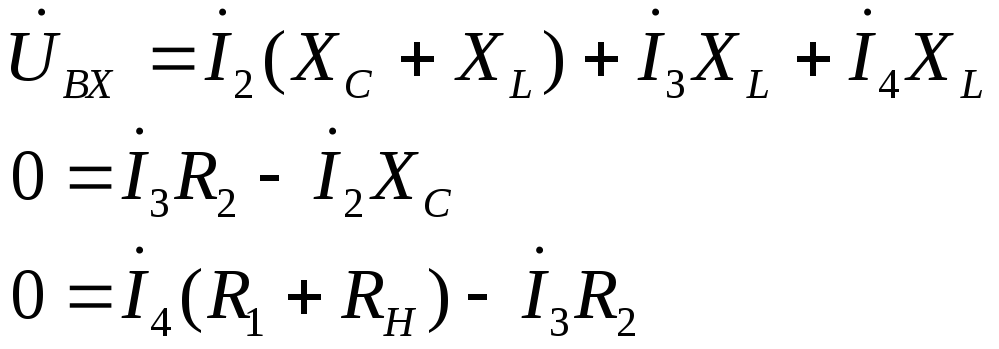
Из третьего уравнения системы находим ток:

.

Подставляем найденный ток в первое уравнение системы и после эквивалентного преобразования система принимает вид :

.

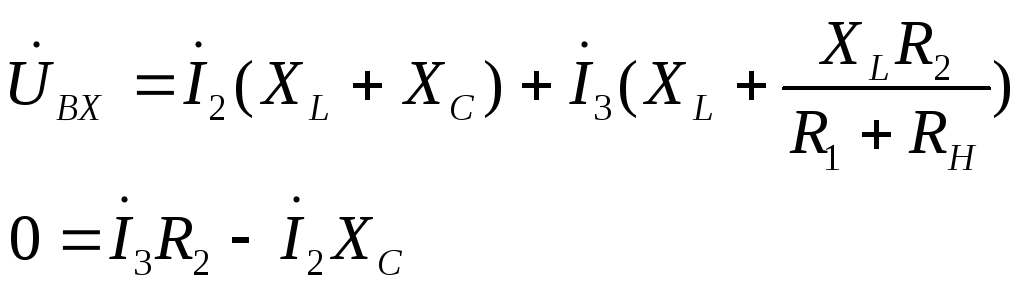Из второго уравнения системы находим ток :

.

Подставляем найденный ток в первое уравнение системы и после эквивалентных преобразований, получаем:

.

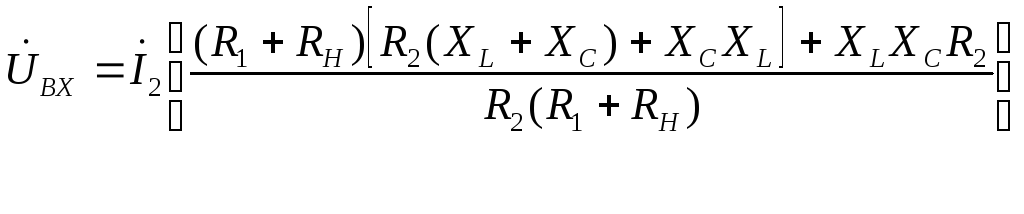
Решаем полеченное уравнение относительно тока :

.

В полученное выражение подставляем численные значения:

.

Осуществляя необходимые преобразования, получаем решение для :

Ток находим по формуле , подставляя в неё численные значения:

.

Ток находим по формуле, подставляя в неё численные значения:

.

Ток находим в соответствии с первым законом Кирхгофа по формуле:

А.

Находим напряжения на элементах:

В.

В.

В.

В.

Сравнивая полученные здесь результаты с результатами предыдущего расчёта, видим, что имеет место достаточно хорошее их совпадение. Однако определим погрешность выполненного расчёта.