Федеральное агентство по образованию РЫБИНСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ имени П.А. СОЛОВЬЕВА
Факультет радиоэлектроники и информатики
Кафедра Радиотехнических и телекоммуникационных систем (КРС) Специальность 230100.62
Пример выполнения расчетно-графической работы
по дисциплине “Общая электротехника и электроника”
на тему
ИССЛЕДОВАНИЕ ЦЕПЕЙ ВТОРОГО ПОРЯДКА
Исполнитель, студент группы		Иванов Е.М.
Работа сдана “___” ________ 2012 г.
Руководитель, канд. техн. наук, доцент		Станевко В.Н.
Оценка “___” ________ 2012 г.
Рыбинск 2012 г.

ОГЛАВЛЕНИЕ

2

1 Задание на расчетно-графическую работу 2

2 Определение величины нагрузки 3

3 Расчёт электрической цепи методом контурных токов 10

4 Расчёт электрической цепи с помощью законов Кирхгофа 14

ЛИТЕРАТУРА 18

1 Задание на расчетно-графическую работу

Выполнить электрический анализ цепи при гармоническом входном воздействии:

1.Определить величину нагрузки для заданной цепи, при которой в неё будет передаваться максимум мощности на заданной частоте. Принять .

2.Расчитать заданную электрическую цепь с учётом при гармоническом входном сигнале:

.

3.Оценить точность расчёта методом баланса мощностей. Погрешность расчёта не должна превышать 1%.

4.По результатам расчёта построить векторную диаграмму и с помощью векторной диаграммы проверить выполнение законов Кирхгофа в рассчитанной схеме.

Рис. 1. Исходная схема

Исходные данные:

f = 2,5 кГц; R₁ = 4 Ом; R₂ = 400 Ом;

С = 2 мкФ; L = 2,0 мГн; U_m = 10 В.

2 Определение величины нагрузки

Из условия задания, величина нагрузки, при которой в неё будет передаваться максимум мощности, должна равняться модулю сопротивления схемы относительно точек 22'. Схема в комплексной форме для определения величины нагрузки представлена на рис.2.

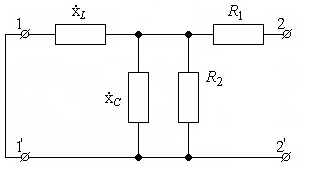
Рис.2 Схема для определения величины нагрузки

Для дальнейшего расчета понадобятся расчетные значения следующих величин:

рад.

Ом

Ом

Определяем сопротивление цепи между точками 22'. Из схемы видно, что элементыXL, иXc соединены параллельно, а они, в свою очередь, соединены последовательно с R1. Тогда сопротивление между точками 22' определяется по формуле:

Подставляем в формулу численные значения:

Теперь можно сразу найти модуль от . Известно, что модуль дроби комплексного числа равен модулю числителя, деленного на модуль знаменателя:

Ом

Ом.

2.1 Расчет электрической цепи

В инженерной практике часто используются следующие методы расчёта – метод эквивалентного преобразования, расчёт с помощью законов Кирхгофа и метод контурных токов. В названной последовательности ниже будет показано применение этих методов к расчёту заданной цепи.

2.2 Расчёт электрической цепи методом эквивалентного преобразования

Основная идея метода состоит в том, что электрическая цепь последовательно преобразуется ("сворачивается") до одного эквивалентного элемента, и определяется входной ток. Затем осуществляется постепенное возвращение к исходной схеме ("разворачивание") с последовательным определением токов и напряжений.

2.3 Последовательность расчёта

1. Расставляются условно–положительные направления токов и напряжений.

2. Поэтапно эквивалентно преобразуются участки цепи. При этом на каждом этапе во вновь полученной после преобразования схеме расставляются токи и напряжения.

3. В результате эквивалентного преобразования определяется величина эквивалентного сопротивления цепи.

4. Определяется входной ток цепи с помощью закона Ома.

5. Поэтапно возвращаясь к исходной схеме, последовательно находятся все токи и напряжения.

В соответствии с рассмотренной последовательностью расчёта, на исходной схеме (рис.3) указываем условно-положительные направления токов и напряжений.

Первым эквивалентным преобразованием будет объединение последовательно соединённых R_н и R1 (рис.4), которое обозначим через .

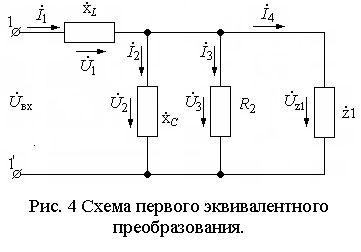
Находим и представляем его в показательной форме:

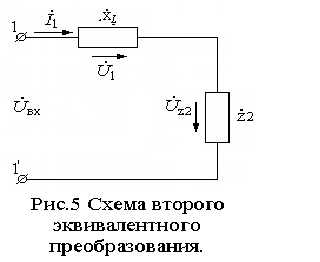
Далее эквивалентно преобразуем (объединяем) три параллельно соединенных элемента ,и, заменяя их сопротивлением(рис.5).

Подставляем численные значения в (2) и выполняем очевидные преобразования. С целью уменьшения преобразований целесообразно в числителе (2) комплексное сопротивление (1) представить в показательной форме, а весь знаменатель представить в алгебраической форме:

.

Входное сопротивление цепи обозначим через и оно будет равно (рис.5):

Подставляя численные значения и выполняя очевидные преобразования, находим :

Находим входной ток по закону Ома. Входное напряжение в комплексной форме имеет вид:

Частоту в выражениях для электрических величин (токи и напряжения) принято не обозначать конкретным числом.

В соответствии со схемой на рис.5, находим напряжения ипо закону Ома:

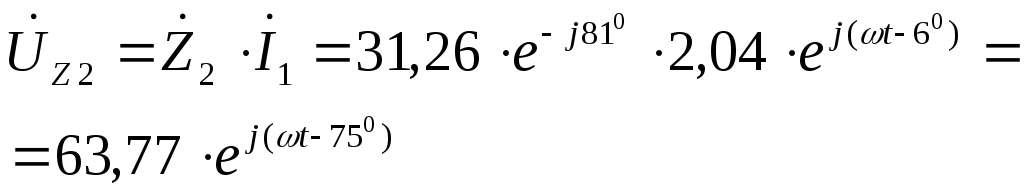
Далее возвращаемся к схеме на рис.4. Сравнивая её со схемой на рис.5, видим, что

Находим токи ,,в параллельных ветвях:

Возвращаемся к исходной схеме на рис.3 и определяем напряжения и: