математикат контр.работа

1.16. Найти интервал сходимости и исследовать на концах

Решение: найдем интервал сходимости данного ряда.

Используем признак Даламбера:

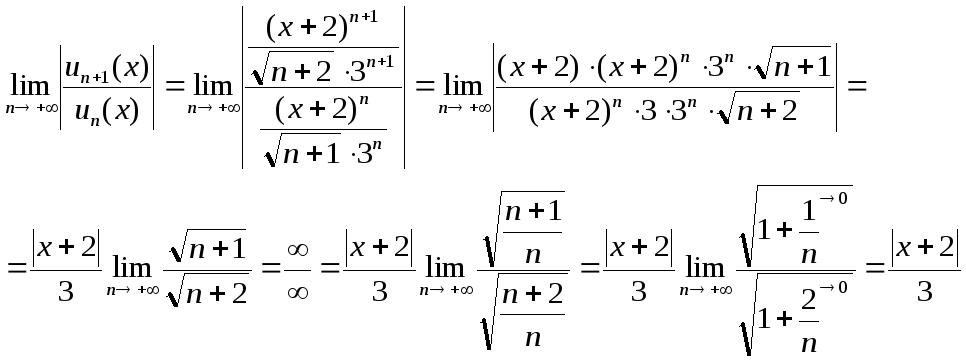
Ряд сходится при

– интервал сходимости исследуемого степенного ряда.

Исследуем сходимость ряда на концах найденного интервала:

1) При

Используем признак Лейбница:

Ряд является знакочередующимся.

– члены ряда убывают по модулю.

Каждый следующий член ряда по модулю меньше, чем предыдущий, то есть убывание монотонно.

Вывод: Ряд сходится по признаку Лейбница.

Исследуем ряд на абсолютную сходимость:

Сравним данный ряд с расходящимся рядом (случай обобщенного гармонического ряда при ). Используем предельный признак сравнения:

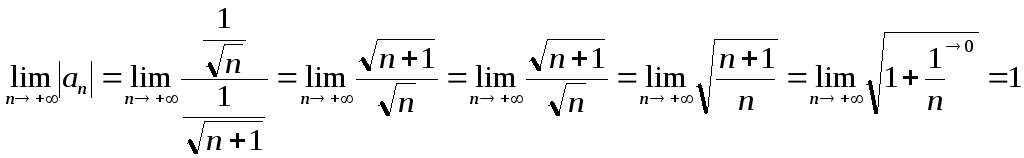
Получено конечное число, отличное от нуля, значит, ряд расходится вместе с рядом .

Таким образом, ряд сходится только условно.

2) При – расходится (по доказанному).

Ответ: область сходимости исследуемого степенного ряда: , при ряд сходится только условно.

2.16. Разложить в степенной ряд по степеням и указать интервал сходимости

Решение: преобразуем функцию:

разложим знаменатель дроби в произведение:

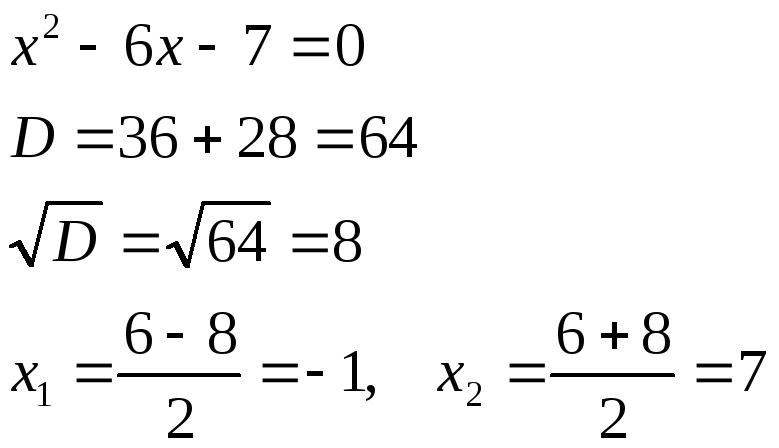
Таким образом:

Методом неопределённых коэффициентов представим функцию в виде суммы дробей:

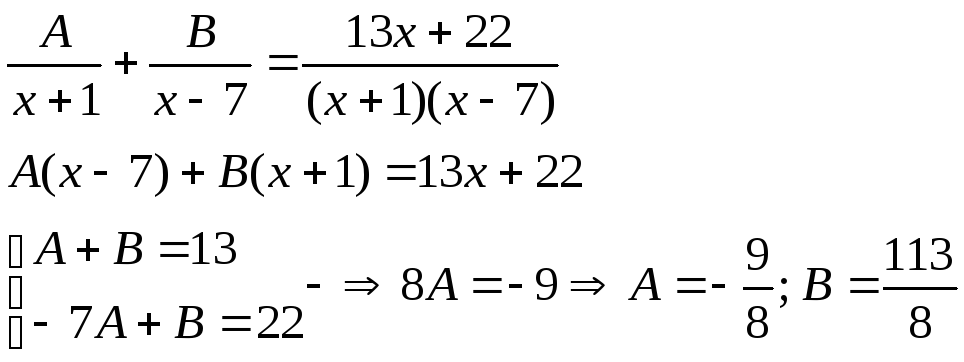
В результате:

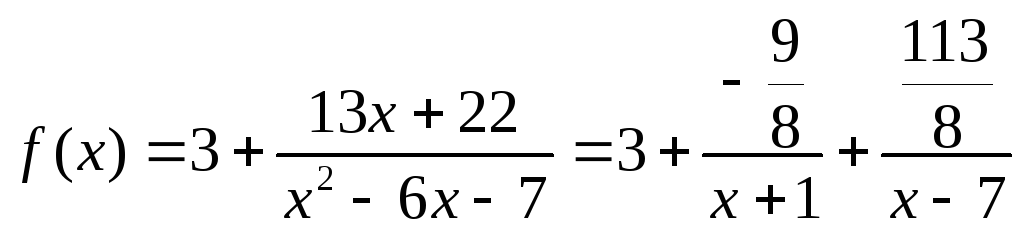
Разложим данную функцию в степенной ряд по степеням .

Используем разложения:

с областью сходимости:

1)

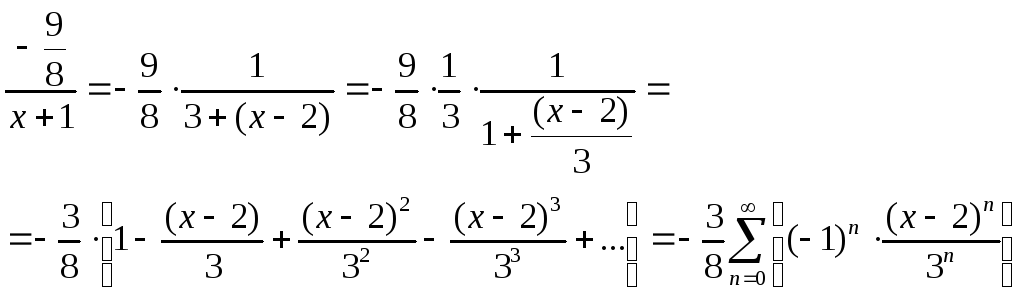
Ряд сходится, если:

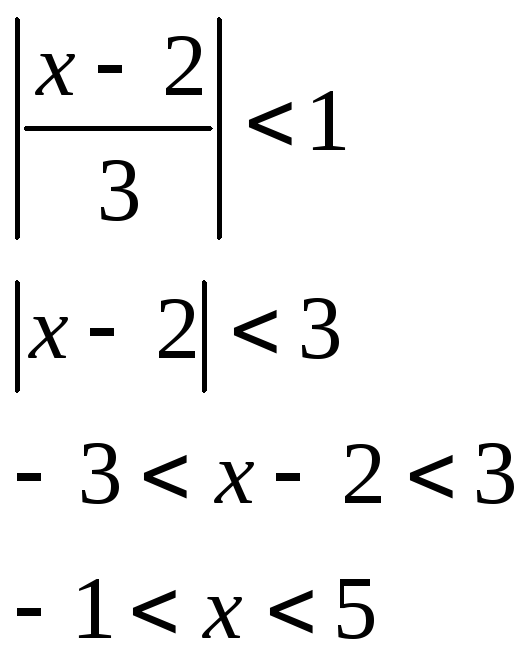
2)

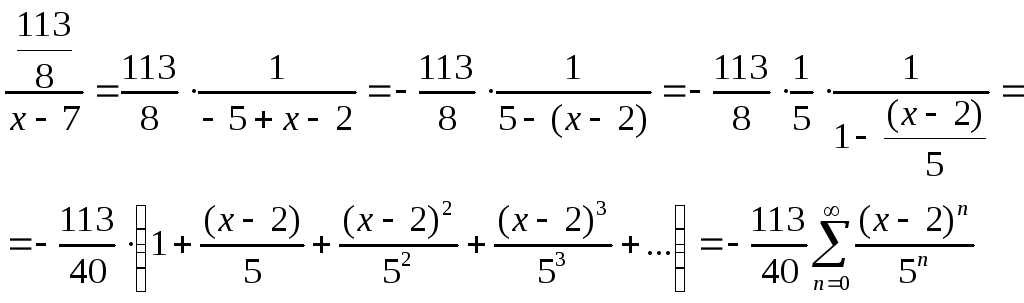
Ряд сходится, если:

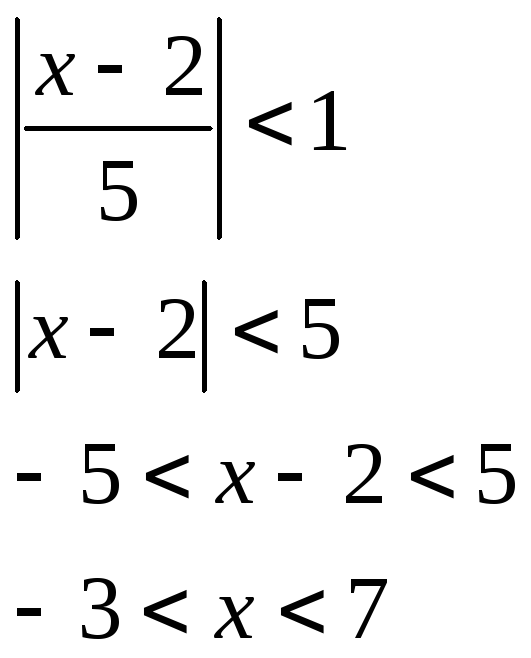
Окончательно:

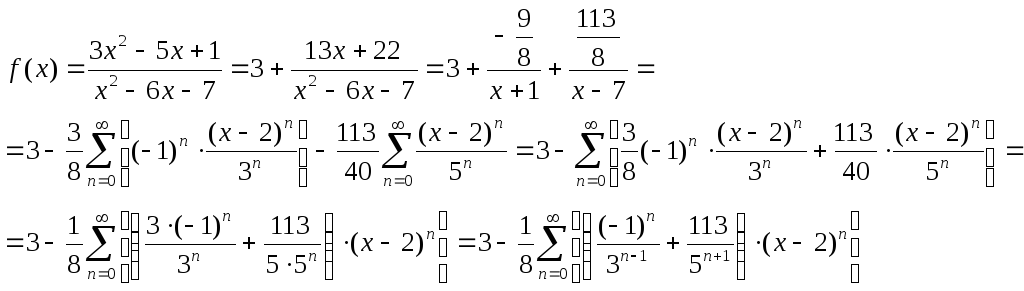
Область сходимости:

Ответ: , ряд сходится, если

3.16. Изменить порядок интегрирования (сделать чертёж области)

Решение: изобразим область интегрирования на чертеже:

Найдём обратные функции:

Изменим порядок обхода области:

1)

Ответ:

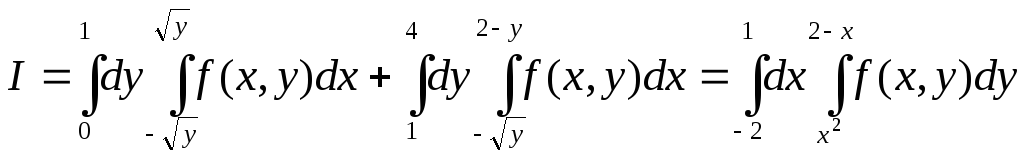
4.16. С помощью двойного интеграла найти площадь фигуры, ограниченной данными линиями (сделать чертёж).

Решение: используем полярную систему координат:

,

Найдём уравнения линий в данной системе:

– окружность радиуса с центром в точке

– окружность радиуса с центром в точке

Найдём точку пересечения окружностей:

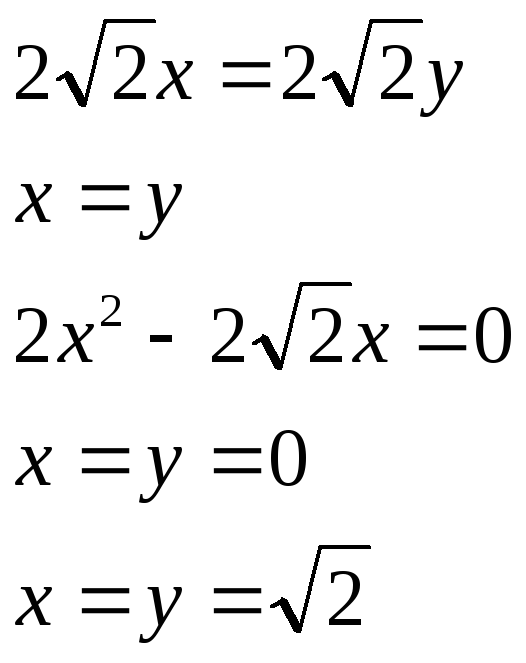
Изобразим область интегрирования на чертеже:

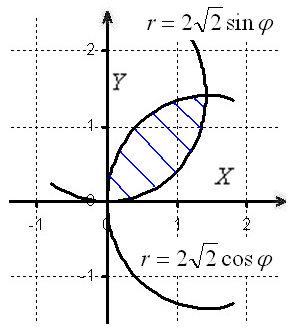
Область интегрирования разделим на две части, порядок обхода:

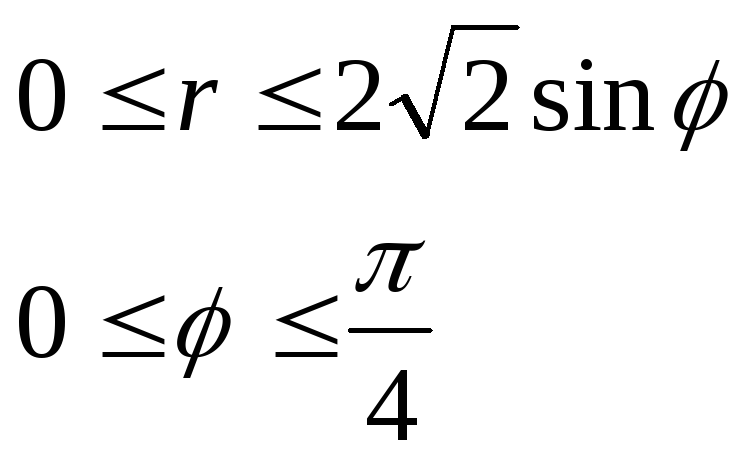
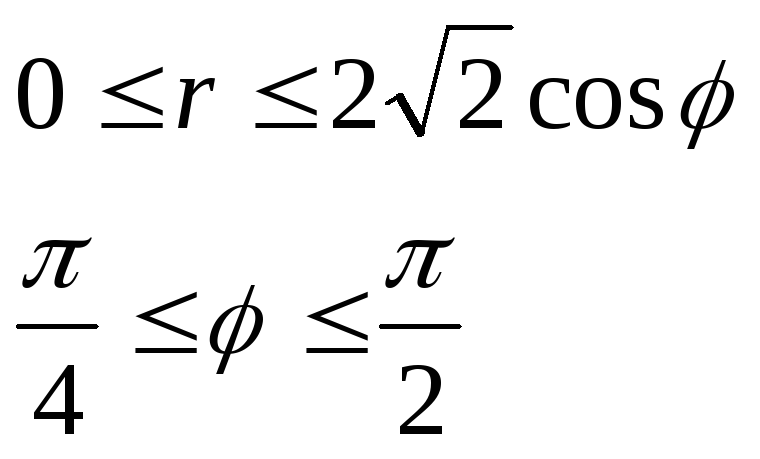
Таким образом:

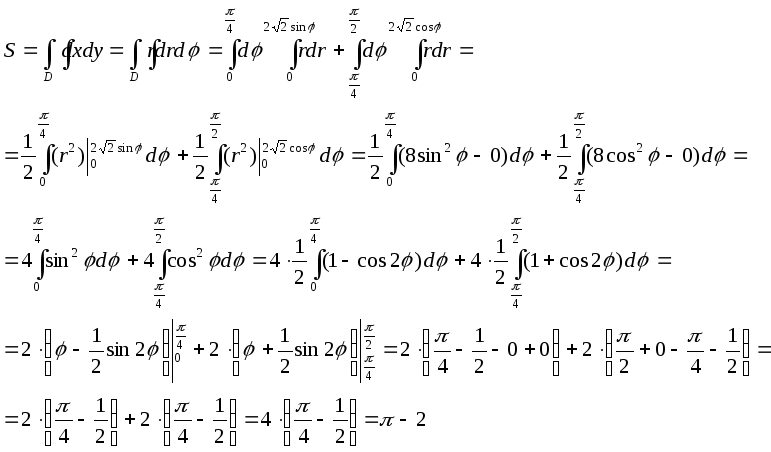
Ответ:

5.16. Найти объем тела, ограниченного заданными поверхностями (сделать схематический чертёж).

Решение: данное тело ограничено эллиптическим параболоидом снизу и конической поверхностью сверху. Найдём линию пересечения поверхностей:

– окружность единичного радиуса.

Проекцией тела на плоскость является круг с центром в начале координат радиуса 1.

Выполним чертёж:

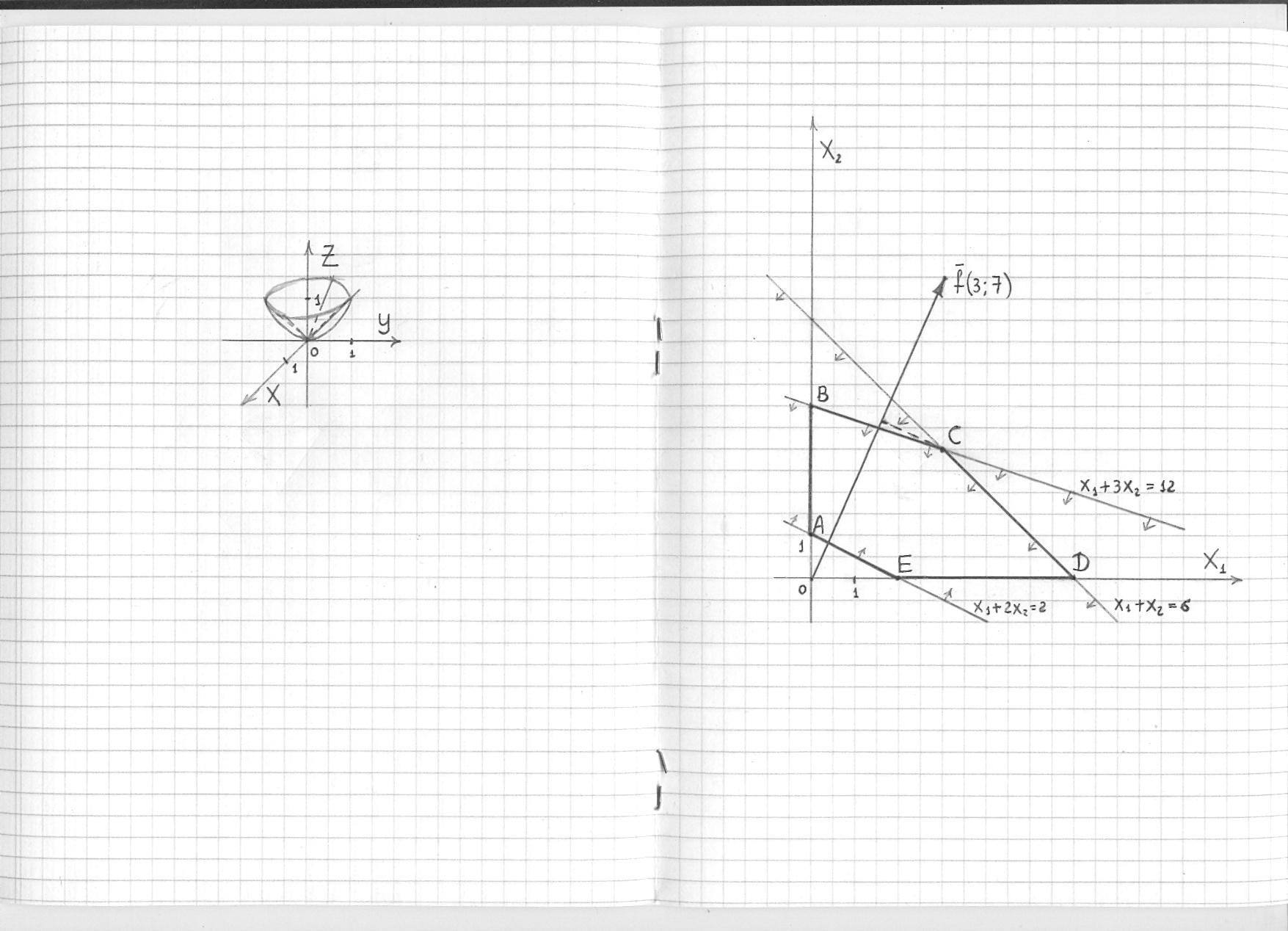
Объем тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат: ,

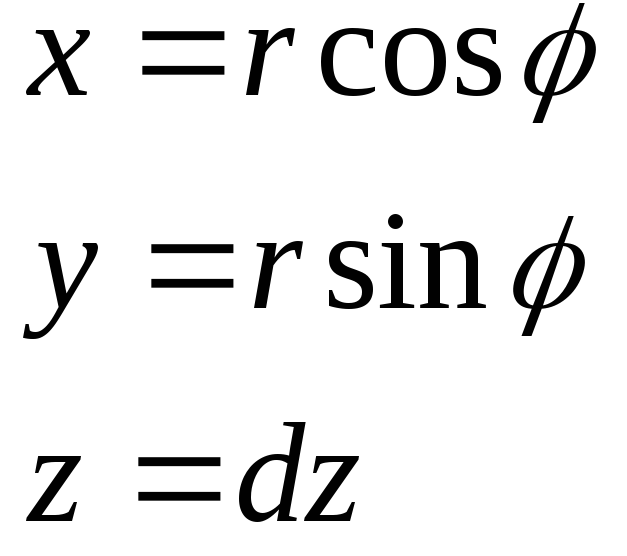Порядок обхода тела:

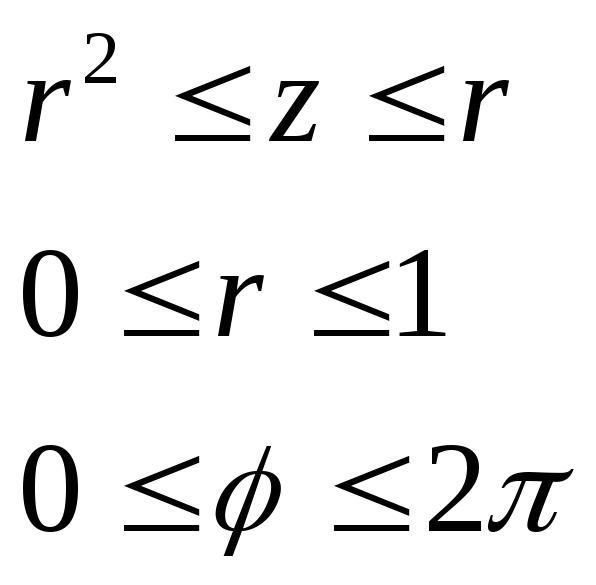
Таким образом:

Ответ:

6.16. Определить, что данное выражение является полным дифференциалом и восстановить с помощью криволинейного интеграла.

Решение: определим, что данное выражение является полным дифференциалом:

, значит, данное выражение является полным дифференциалом функции.

Найдём данную функцию с помощью криволинейного интеграла, выбрав точку :

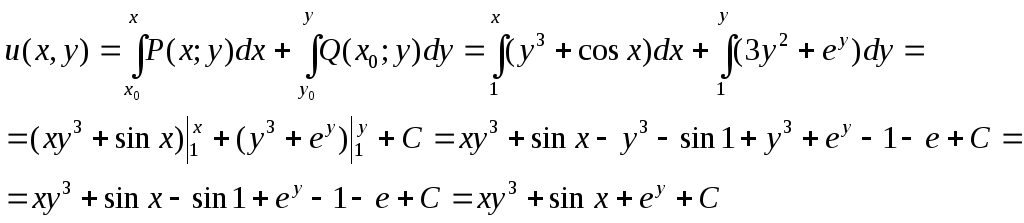
( – это тоже некоторая константа )

Ответ: