
- •Колебания. Волны. Оптика
- •1.Колебания
- •1.1.Гармонические колебания
- •1.1.1. Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний
- •1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний
- •1.1.3. Примеры колебательных движений различной физической природы
- •1.1.3.1. Колебания груза на пружине
- •Где – коэффициент жёсткости пружины, – координата положения равновесия, х – координата груза (материальной точки) в момент времени ,- смещение от положения равновесия.
- •1.1.3.2. Маятники
- •1.1.4. Сложение колебаний (биения, фигуры Лиссажу). Векторное описание сложения колебаний
- •1.1.5. Энергия колебаний
- •1.2. Ангармонический осциллятор
- •1.2.1. Линейность и принцип суперпозиции. Границы его применимости
- •1.2.2. Ангармонический осциллятор
- •1.3. Свободные затухающие колебания осциллятора с потерями
- •Она пропорциональна числу колебаний за время релаксации.
- •1.4. Вынужденные колебания. Время установления вынужденных колебаний. Его связь с добротностью осциллятора
- •1.5.Электромагнитные процессы в колебательном контуре с током
- •1.5.1. Свободные колебания в контуре
- •1.5.2. Свободные затухающие колебания в контуре
- •1.5.3. Вынужденные электрические колебания. Резонанс в последовательном контуре
- •1.5.4.Резонанс в параллельном контуре
- •1.5.5.Переменный ток
- •1.6.Связанные колебания. Нормальные моды связанных осцилляторов
- •1.6.1.Системы с двумя степенями свободы Нормальные моды колебаний
- •1.6.2.Общее решение для мод
- •2.Волны в упругой среде
- •2. 1. Волновое движение. Продольные и поперечные волны
- •2.2. Волновое уравнение в пространстве. Плоская гармоническая волна. Длина волны, волновое число, фазовая скорость. Одномерное волновое уравнение. Упругие волны в газах, жидкостях и твердых телах
- •2.3.Энергия волны
- •2.4.Принцип суперпозиции волн
- •2.5.Образование стоячих волн
- •2.6.Свободные колебания системы со многими степенями свободы. Волны – колебания непрерывных систем
- •2.7. Стоячие волны как нормальные моды колебаний
- •2.8. Моды поперечных колебаний непрерывной струны
- •2.9. Эффект Доплера
- •2.10. Электромагнитные волны
- •2.10.2. Энергетические характеристики электромагнитных волн. Вектор Пойнтинга
- •2.10. 2.1.Энергия и импульс электромагнитного поля. Сохранение энергии и импульса в изолированной системе произвольно движущихся зарядов
- •2.10.2.2. Работа, совершаемая полем при перемещении зарядов
- •2.10.2.3.Энергия электромагнитного поля. Плотность и поток энергии. Закон изменения энергии
- •2.10.2.4. Закон сохранения энергии для изолированной системы «поле- заряды»
- •2.10.2.5. Импульс электромагнитного поля. Закон сохранения импульса и момента импульса
- •2.10.3 Излучение диполя
2.7. Стоячие волны как нормальные моды колебаний
Моды непрерывных систем называются стоячими волнами. Непрерывная система имеет бесконечное число независимых элементов и обладает бесконечным числом мод. Общее движение системы может быть описано как суперпозиция всех её мод с амплитудами и фазами колебаний, определяемыми из начальных условий.
Рассмотрим поперечные колебания струны с грузами. Под струной мы подразумеваем пружину. Рассмотрим линейные (подчиняющиеся закону Гука) невесомые пружины, на которых расположены массы М(грузы).
На рисунке 2.5 представлена последовательность таких струн с N=1,2,3,4, и показаны конфигурации, соответствующие нормальным модам.
В m-ной моде положение равновесия пересекается струной (m-1) раз и мода состоит изmполуволн. Мода с самой большой частотой соответствует кривой с «зигзагами».
Если принять, что показанные конфигурации совпадают с конфигурациями мод, то мы правильно расположили конфигурации в порядке возрастания частоты мод.
Последовательность предполагаемых мод образует именно Nконфигураций: число узловых точек (точки, в которых пружина пересекает горизонтальную ось, включая концевые точки) равно нулю в первой моде, вторая мода имеет одну узловую точку и т.д. Самая высокая мода имеетN-1 узловых точек.
2.8. Моды поперечных колебаний непрерывной струны
Рассмотрим
случай, когда Nвелико,
тогда для двух первых мод между двумя
соседними узлами окажется очень много
грузов. Смещение будет медленно меняться
от одного груза к другому, тогда можно
считать, что все частицы в окрестности
точки (x,y,z),
соответствующей положению равновесия
имеют один и тот же мгновенный вектор
смещения![]() .
Координатыx,y,zпредставляют собой равновесное состояние
частиц и не зависят от времени.
.
Координатыx,y,zпредставляют собой равновесное состояние
частиц и не зависят от времени.
Пусть в состоянии равновесия струна растянута вдоль оси Х. Тогда координатахдаёт положение равновесия каждого груза:
![]() ,
,
смещение
вдоль оси Х
-продольное,
а вдоль осей Z
и Y
- поперечное.
Для поперечных колебаний струны
![]() ,
поэтому:
,
поэтому:
![]() .
.
Для простоты положим, что колебания происходят только вдоль оси Z (Ψy=0). В этом случае говорят, что колебания линейно поляризованы вдоль оси Z.
Попытаемся
найти нормальные моды непрерывной
струны, которые представляют собой
стоячие волны. Предположим, что мы
возбудили какую-то моду, и все части
струны совершают гармоническое движение
с одинаковой частотой ω
и одинаковой
фазовой постоянной φ.
Тогда функция
![]() ,
представляющая собой смещение частиц,
которые в равновесии находятся вх,
должна иметь одну и ту же временную
зависимость вида cos(ωt+φ)
для всех движущихся элементов, то есть
для всех х.
Как обычно, фазовая постоянная
соответствует моменту включения моды.
«Геометрия» моды зависит от числа
степеней свободы a,
b,
c
…и т.д. и
определяется отношением амплитуд
колебаний А,
В, С …и т.д.,
соответствующим этим степеням.
,
представляющая собой смещение частиц,
которые в равновесии находятся вх,
должна иметь одну и ту же временную
зависимость вида cos(ωt+φ)
для всех движущихся элементов, то есть
для всех х.
Как обычно, фазовая постоянная
соответствует моменту включения моды.
«Геометрия» моды зависит от числа
степеней свободы a,
b,
c
…и т.д. и
определяется отношением амплитуд
колебаний А,
В, С …и т.д.,
соответствующим этим степеням.
В случае непрерывной струны амплитуда колебаний для различных степеней свободы (то есть геометрия моды) может быть представлена в виде непрерывной функции от х – А(х). Функция А(х) характеризует моду; каждой моде соответствует своя А(х), тогда общее выражение для стоячей волны имеет вид:
![]() =А(х)
cos(ωt+φ).
(2.15)
=А(х)
cos(ωt+φ).
(2.15)
Для ускорения получаем:
![]() (2.16)
(2.16)
Вторая производная (2.15) по х равна
![]() (2.17)
(2.17)
Здесь знак частной производной ∂ заменен знаком полной производной d, так как А не зависит от времени.
Подставим
(2.16) и (2.17) в общее уравнение волны и
заменим y
на
![]() :
:
![]()
тогда
имеем:
![]() Сократив на cos(ωt+φ)
и на
Сократив на cos(ωt+φ)
и на
![]() ,
получаем
,
получаем
![]() ,
или
,
или
![]() .
.
Это
уравнение определяет геометрическую
форму моды. Здесь
![]() – волновое число, поэтому
– волновое число, поэтому
![]() тогда
тогда
![]() (2.18)
(2.18)
-каждой моде (то есть частоте ω) соответствует своя форма.
Уравнение (2.18) совпадает с уравнением гармонического осциллятора, в котором время заменено координатой. Решение этого уравнения имеет вид:
![]()
Тогда
![]() (2.19)
(2.19)
Дополним
выражение (2.19) граничными условиями.
Струна закреплена на концах, то есть
при x=0
и x=L
![]() :
:
![]() отсюда
В=0
и
отсюда
В=0
и
![]()
![]() ,
тогда
,
тогда
![]() ,
и
,
и
![]() Получаем
условие образования стоячих волн в
струне – по длине струны укладывается
целое число полуволн. Из него имеем:
Получаем
условие образования стоячих волн в
струне – по длине струны укладывается
целое число полуволн. Из него имеем:
![]()
-это длины волн всех возможных мод, возникающих в струне.
Для
частот имеем:
![]()
Частоты
![]() и т.д. называются второй, третьей и т.д.
гармониками основной частоты
и т.д. называются второй, третьей и т.д.
гармониками основной частоты![]() ,
соответствующих первой моде колебаний.
,
соответствующих первой моде колебаний.
Важно
помнить, что для всех гармоник (для всех
мод) выполняется соотношение
![]() ,
где
,
где![]() – фазовая скорость волны. Заменив
– фазовая скорость волны. Заменив
![]() ,
получаем
,
получаем
![]() – это уравнение определяетω
как функцию волнового числа
– это уравнение определяетω
как функцию волнового числа
![]() и называется дисперсионным соотношением
или законом дисперсии. При этом
и называется дисперсионным соотношением
или законом дисперсии. При этом
![]() в
общем случае не остается постоянной.
в
общем случае не остается постоянной.
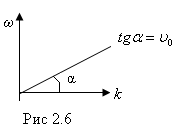 Волны,
удовлетворяющие простому дисперсному
соотношениюω/k=const,
называют недиспергирующими волнами.
Волны,
удовлетворяющие простому дисперсному
соотношениюω/k=const,
называют недиспергирующими волнами.
Если
отношение ω/k
зависит от
длины волны, а значит и от частоты, то
волны называют диспергирующими. График
зависимости ω
от
![]() в случае упругой струны представляет
собой прямую линию, выходящую из начала
координат.
в случае упругой струны представляет
собой прямую линию, выходящую из начала
координат.
