
1.4. Закон ома для неоднородного участка цепи
На
носители тока на неоднородном участке
цепи действуют, кроме электростатических
сил
![]() ,
еще и сторонние силы
,
еще и сторонние силы![]() .
Сторонние силы способны вызывать
упорядоченное движение носителей тока
так же, как и силы электростатические.
На неоднородном участке цепи средняя
скорость упорядоченного движения
носителей пропорциональна суммарной
силе
.
Сторонние силы способны вызывать
упорядоченное движение носителей тока
так же, как и силы электростатические.
На неоднородном участке цепи средняя
скорость упорядоченного движения
носителей пропорциональна суммарной
силе![]() ,
тогда плотность тока
,
тогда плотность тока
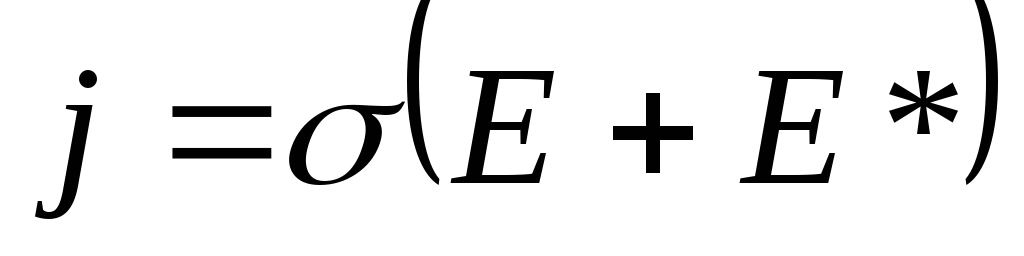 (2)
(2)
– это закон Ома для неоднородного участка цепи в дифференциальной форме.
Перейдем к интегральной форме этого закона. Рассмотрим неоднородный участок цепи. Допустим, что внутри этого участка существует линия (контур тока) удовлетворяющая следующим условиям:
в каждом сечении, перпендикулярном к контуру, величины
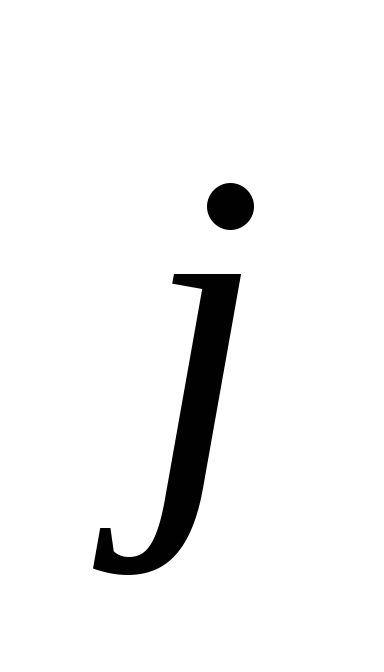 ,
, ,
, и
и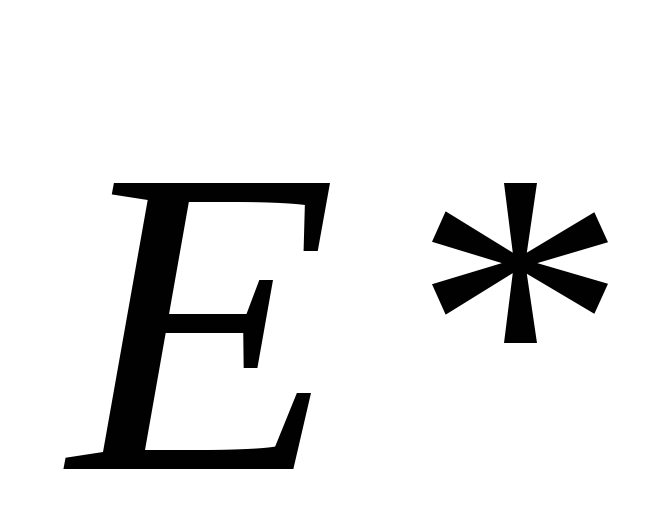 имеют
с достаточной точностью одинаковые
значения;
имеют
с достаточной точностью одинаковые
значения;векторы
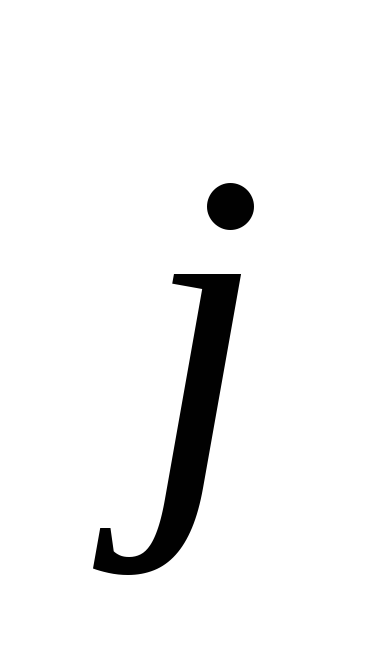 ,
, ,
,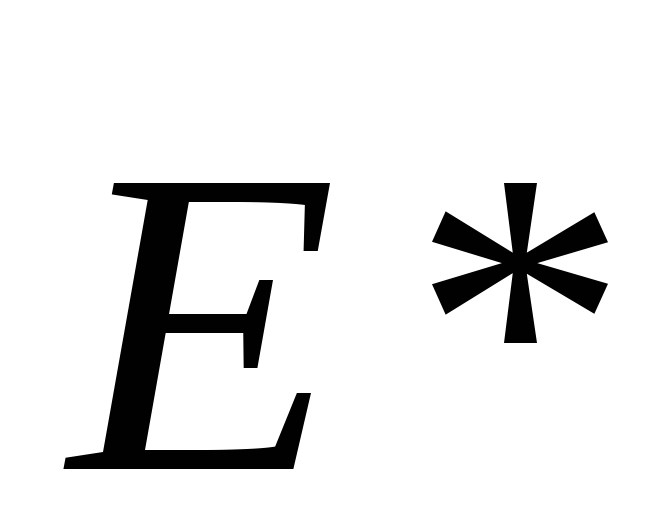 в каждой точке направлены по касательной
к контуру. Поперечное сечение проводника
может быть непостоянным.
в каждой точке направлены по касательной
к контуру. Поперечное сечение проводника
может быть непостоянным.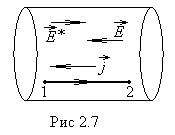 Выберем произвольно
направление движения по контуру. Пусть
выбранное направление соответствует
перемещению от конца 1 к концу 2 участка
цепи. Спроектируем выражение (2) на
элемент контура1-2:
Выберем произвольно
направление движения по контуру. Пусть
выбранное направление соответствует
перемещению от конца 1 к концу 2 участка
цепи. Спроектируем выражение (2) на
элемент контура1-2:
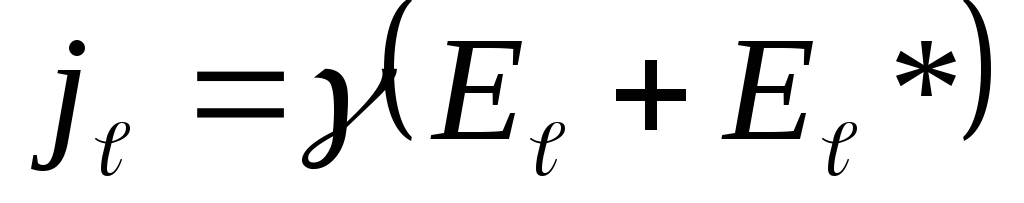 ,
(3)
,
(3)
причем
![]() ;
;
![]() ;
;
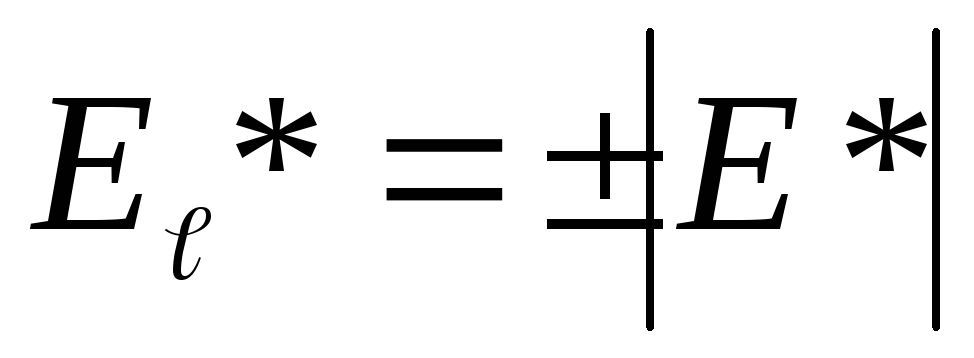 .
Знак «+» берем в том случае, если ток
течет от 1 к 2, «-»если ток течет в
направлении 2 к 1. Вследствие сохранения
заряда сила постоянного тока в каждом
сечении должна быть одинаковой. Поэтому
вдоль контура
.
Знак «+» берем в том случае, если ток
течет от 1 к 2, «-»если ток течет в
направлении 2 к 1. Вследствие сохранения
заряда сила постоянного тока в каждом
сечении должна быть одинаковой. Поэтому
вдоль контура
![]() .
Силу тока в данном случае нужно
рассматривать как алгебраическую
величину. Направление 1-2 выбрано
произвольно, поэтому, если ток течет в
выбранном направлении, его считают
положительным, если в направлении 2-1 –
отрицательным. Заменим
.
Силу тока в данном случае нужно
рассматривать как алгебраическую
величину. Направление 1-2 выбрано
произвольно, поэтому, если ток течет в
выбранном направлении, его считают
положительным, если в направлении 2-1 –
отрицательным. Заменим
![]() ;
;
![]() ,
тогда из ( 3):
,
тогда из ( 3):
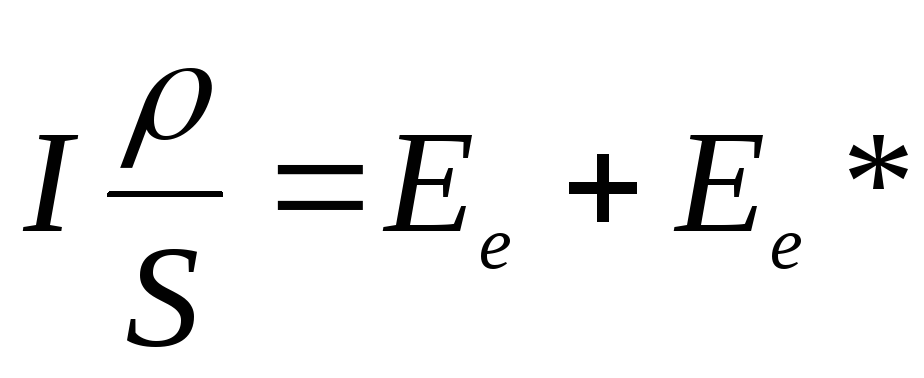 .
.
Умножим
это выражение на
![]() и проинтегрируем вдоль контура:
и проинтегрируем вдоль контура:
![]() .
.
Здесь
![]() – сопротивление всей цепи,
– сопротивление всей цепи,![]() - разность потенциалов на сопротивлениеR,
- разность потенциалов на сопротивлениеR,
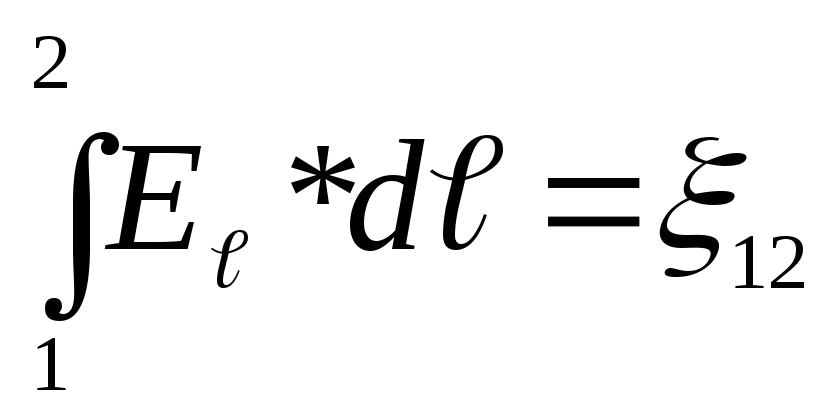 - ЭДС, действующая на участки 1,2. Тогда
- ЭДС, действующая на участки 1,2. Тогда
![]() ,
а ток
,
а ток
![]()
– это закон Ома для неоднородного участка цепи.
Если
цепь замкнутая, то
![]() ;
и
;
и
![]() .Тогда
.Тогда
![]() -закон Ома для замкнутой цепи. Если в
цепи действует несколько ЭДС, то
-закон Ома для замкнутой цепи. Если в
цепи действует несколько ЭДС, то
![]() равна их алгебраической сумме.
равна их алгебраической сумме.
1.5. Мощность тока
Рассмотрим
произвольный участок цепи постоянного
тока, к концам которого приложено
напряжение U.
За
время t
через каждое сечение проводника проходит
заряд
q=It,что
равносильно переносу заряда q
из одного конца проводника на другой.
При этом силы электростатического поля
и сторонние силы совершают работу
![]() ,
тогда мощность
,
тогда мощность
![]() .
.
Эта мощность может расходоваться на совершение работы участком цепи над внешними телами
( для этого участок должен перемещаться в пространстве), на протекание химической реакции и на перемещение данного участка цепи.
Отношения мощности dp , развиваемой в объеме dV, к величине этого объема, называется удельной мощностью тока
![]() .
.
Найдем
выражение для удельной мощности тока.
Сила
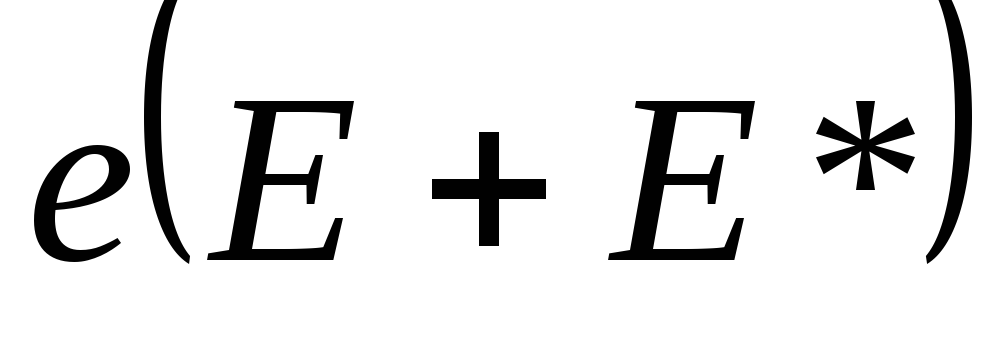 развивает при движении носителя тока
мощность:
развивает при движении носителя тока
мощность:
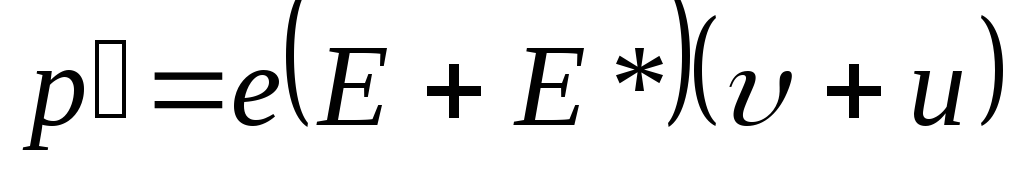 ,
,
где
![]() – скорость хаотического движения,
– скорость хаотического движения,![]() – скорость упорядоченного движения
носителей.
– скорость упорядоченного движения
носителей.
Усредним
это выражение по носителям, заключенным
в объеме dV,
в пределах которого
![]() и
и![]() можно считать постоянными:
можно считать постоянными:
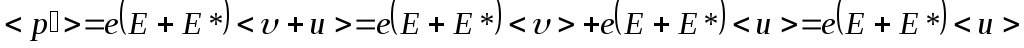 .
.
Мощность
![]() , развиваемую в объеме
, развиваемую в объеме![]() , найдем, умножив
, найдем, умножив![]() на число носителей тока в этом объеме
:
на число носителей тока в этом объеме
:
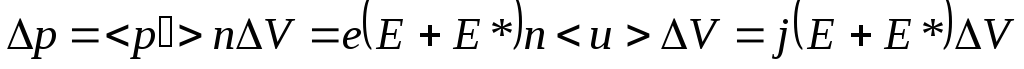 .
.
Подставив
![]() ,
имеем:
,
имеем:
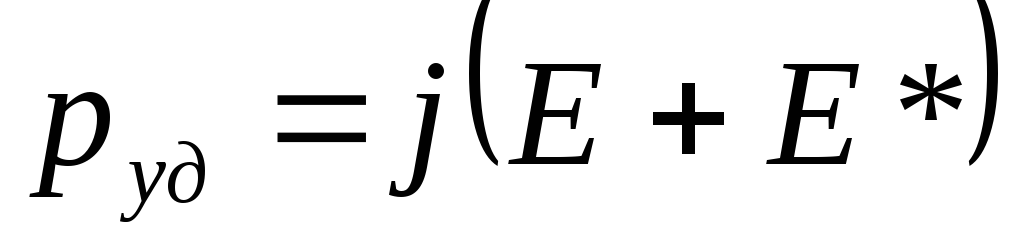
1.6. ЗАКОН ДЖОУЛЯ –ЛЕНЦА
Если ток в цепи постоянен, а проводники, входящие в цепь, неподвижны, работа сторонних сил полностью расходуется на нагревание проводников. Тепловую энергию обозначим W.
Объемной
плотностью тепловой мощности тока
![]() называется энергия, выделяющаяся в
единице объема проводника за единицу
времени.Закон
Джоуля -Ленца в дифференцированной
форме имеет вид:
называется энергия, выделяющаяся в
единице объема проводника за единицу
времени.Закон
Джоуля -Ленца в дифференцированной
форме имеет вид:
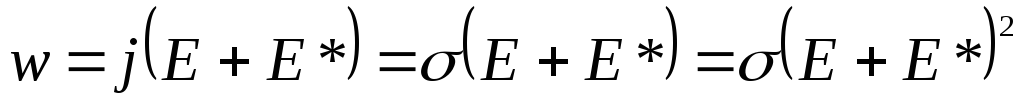
-
объемная плотность тепловой мощности
тока равна скалярному произведению
векторов плотности тока
![]() и напряженности электрического поля.
и напряженности электрического поля.
Объемная плотность тепловой мощности тока прямо пропорциональна квадрату напряженности электрического поля, создающего ток, и удельной проводимости проводника.
Интегрируя это выражение по объему проводника, получим закон Джоуля –Ленца в интегральной форме: количество теплоты, выделяемой в проводнике, пропорционально силе тока, времени его прохождения и падению напряжения:
![]() .
.
Классическая электронная теория дает следующее объяснение рассматриваемому выше закону. Кинетическая энергия электрона в конце пробега
![]() .
.
При
столкновении с ионом кристаллической
решетки электрон отдает свою энергию,
поэтому внутренняя энергия металла
возрастает (металл нагревается), число
соударений одного электрона
![]() ,
поэтому в единицу времени в единице
объема выделяется тепло:
,
поэтому в единицу времени в единице
объема выделяется тепло:
![]() .
.
Для
энергии dW
имеем:
![]() ,
причем объём
,
причем объём
![]() .
.
Проинтегрировав
это выражение, получаем:
![]() ,
причем
,
причем
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
Таким образом, количество теплоты, выделяемой в проводнике, равно
![]() .
.
Рассмотрим
электрическую цепь, состоящую из
источника тока с эдс
![]() и внутренним сопротивлениемr
и нагрузки сопротивлением R
(рис. 7).
и внутренним сопротивлениемr
и нагрузки сопротивлением R
(рис. 7).
По закону Ома ток в цепи равен:
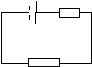
![]() .
.
Напряжения на нагрузке U совпадает с напряжением на зажимах источника и равно:
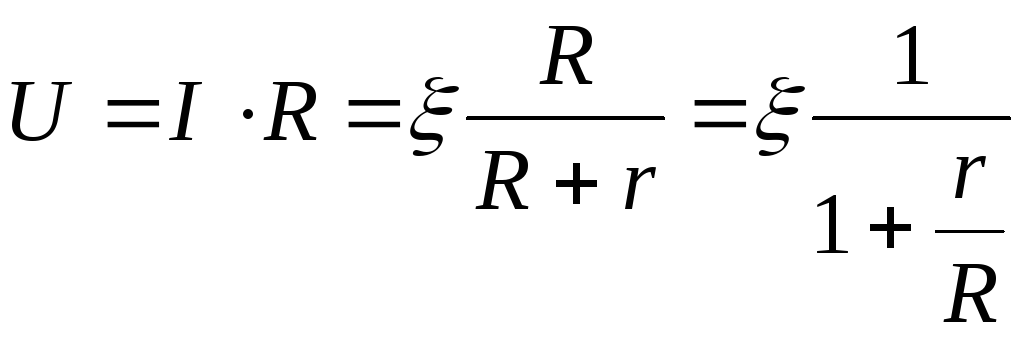 .
.
Напряжение
U
всегда меньше
![]() ,
если цепь разомкнута,R→∞
и U=
,
если цепь разомкнута,R→∞
и U=
![]() .
.
Полная мощность, развиваемая в цепи источником тока равна
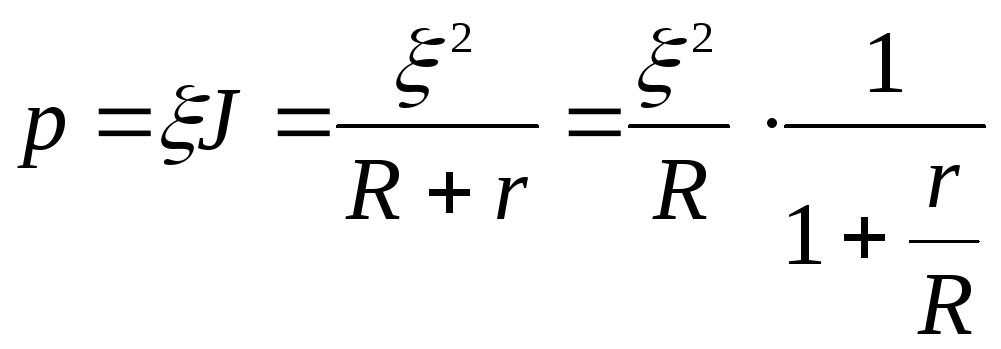 .
(4)
.
(4)
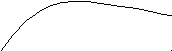
Зависимость
полной мощности по отношению
![]() представлена на рис. 8.
представлена на рис. 8.


![]()
Рис.8
На нагрузке выделяется не вся мощность р, а часть её, называемая полезной:
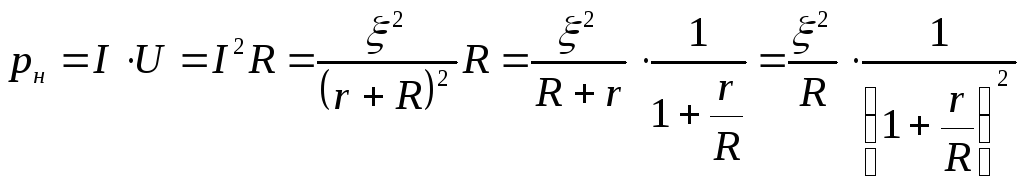 .
(5)
.
(5)
Полезная
мощность имеет максимальные значения,
когда производная функции
![]() по переменнойR
равна нулю:
по переменнойR
равна нулю:
![]() .
Это имеет место приR=r.
.
Это имеет место приR=r.
Зависимость
полезной мощности от отношения
![]() представлена на рис. 9.
представлена на рис. 9.
р н
н

![]()

1
η
1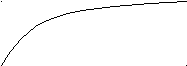

0

 ,5
,5
 1
1
![]()
Рис. 10
КПД
будет тем больше, чем меньше отношение
![]() ,
т.е. чем больше сопротивление нагрузкиR.
При размыкании цепи R→∞
и η=1.
,
т.е. чем больше сопротивление нагрузкиR.
При размыкании цепи R→∞
и η=1.
О днако
при этом мощность, выделяемая во внешней
цепи, стремиться к нулю, поэтому условие
максимума КПД с практической точки
зрения не интересно. Наиболее притягательная
областьR~r0
, в которой
полезная мощность наибольшая и η~0,5.
днако
при этом мощность, выделяемая во внешней
цепи, стремиться к нулю, поэтому условие
максимума КПД с практической точки
зрения не интересно. Наиболее притягательная
областьR~r0
, в которой
полезная мощность наибольшая и η~0,5.
2.ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ИЗМЕРЕНИЙ
Для исследования мощности используется лабораторная установка (рис.11), выполненная в виде прибора настольного типа и содержащая смонтированные в одном корпусе специализированный источник питания, который по своим характеристикам является аналогом аккумулятора; стрелочный вольтмиллиамперметр с пределами измерений напряжения от 0 до 25В; нагрузка-реостат с сопротивлением несколько сот Ом. Питание установки осуществляется от сети напряжением 220 В. На лицевой панели прибора (рис. 11) расположены клавиша 1 включения источника питания «ВКЛ», под которой помещена сигнальная лампочка 2, шкала вольтмиллиамперметра 3, переключатель 4 измерений I/U, ручки потенциометра 5. В положении «I» переключателя 4 стрелочный прибор показывает силу тока, в положении «U» - напряжение на нагрузке. Потенциометр R меняет сопротивление нагрузки от нуля до максимального значения.
Схема установки представлена на рис. 12.
3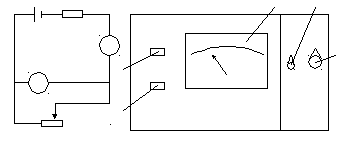 4
4
![]() r
r
5
2 мА
I U
V 1 ВКЛ
R
Рис. 12
Установка включается в сеть напряжением 220В.
В работе предусматривается определение внутреннего сопротивления r и ЭДС источника двумя способами – графическим и расчетным.
Графический метод определения внутреннего сопротивления и ЭДС источника состоит в следующем. Меняя сопротивление реостата R потенциометром, фиксируют соответствующие значения тока J и напряжения на нагрузке. По формуле
pН = IU (6)
вычисляют полезную мощность, а по формуле
![]() (7)
(7)
сопротивление нагрузки, и строят зависимость pН(R) . По графику определяют сопротивление R, при котором pН достигает максимума. В этом случае R = r.
По закону Ома
![]() (8)
(8)
- по этой формуле вычисляют ЭДС источника.
Зная
R
и
r,
строят зависимости
![]() ,
,![]() ,
,![]() .
При этом должно выполняться соотношение(1)
= 0,5.
.
При этом должно выполняться соотношение(1)
= 0,5.
Более
точный метод определения r
и
![]() основан
на применении метода наименьших квадратов
(МНК) и включает в себя обработку
результатов эксперимента на ЭВМ (см.
Приложение 1). По данным эксперимента
строят зависимость
основан
на применении метода наименьших квадратов
(МНК) и включает в себя обработку
результатов эксперимента на ЭВМ (см.
Приложение 1). По данным эксперимента
строят зависимость
![]() и апроксимируют ее прямой, уравнение
которой имеет вид:
и апроксимируют ее прямой, уравнение
которой имеет вид:
![]() .
.
Напряжение
U
откладывают по оси ординат, ток I
– по оси абсцисс. Точка пересечения
этой прямой с осью ординат соответствует
значению
![]() ,
тангенс
угла наклона к оси абсцисс – сопротивлению
r.
,
тангенс
угла наклона к оси абсцисс – сопротивлению
r.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Проверив подключение реостата к клеммам установки, включить сетевой шнур в розетку. На лицевой панели включить клавишу 1 «ВКЛ». При этом должна загореться сигнальная лампочка 2.
Перемещая движок реостата и изменяя напряжение от минимума до 20 зафиксировать не менее 10 значений тока
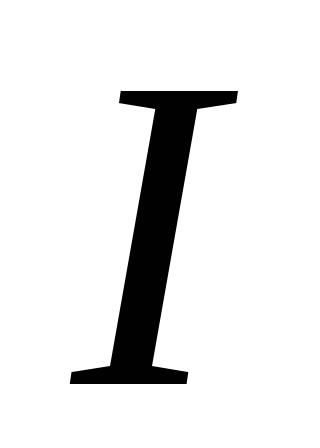 и напряжения
и напряжения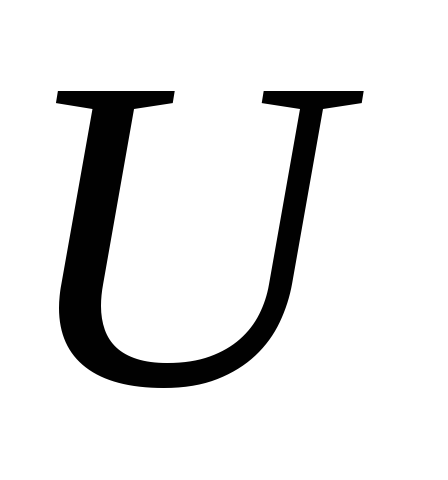 .
.Отключить установку в последовательности, обратной процедуре включения.
По результатам измерений рассчитать значения сопротивления нагрузки
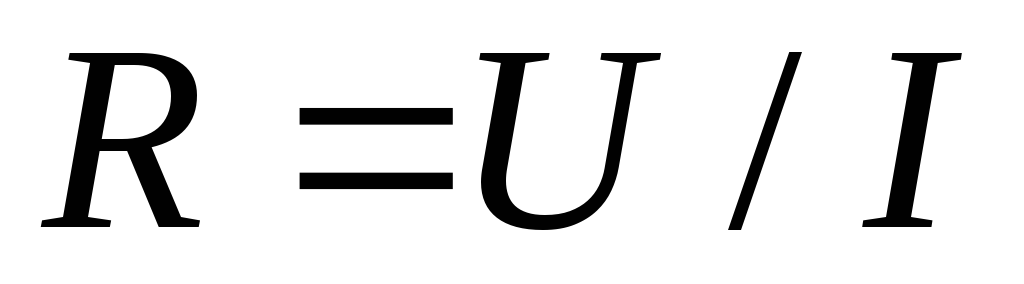 ,
полезной мощности
,
полезной мощности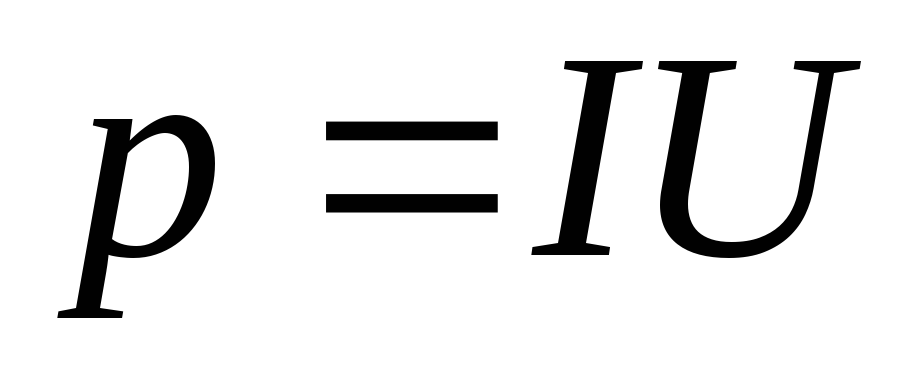 ,
полной мощности
,
полной мощности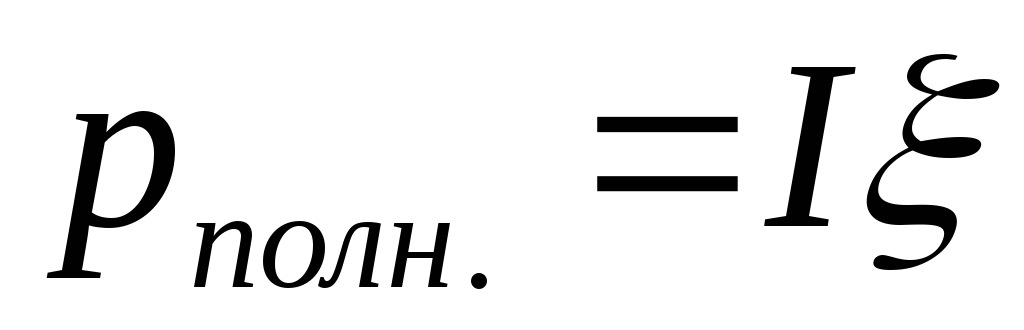 (полагая
(полагая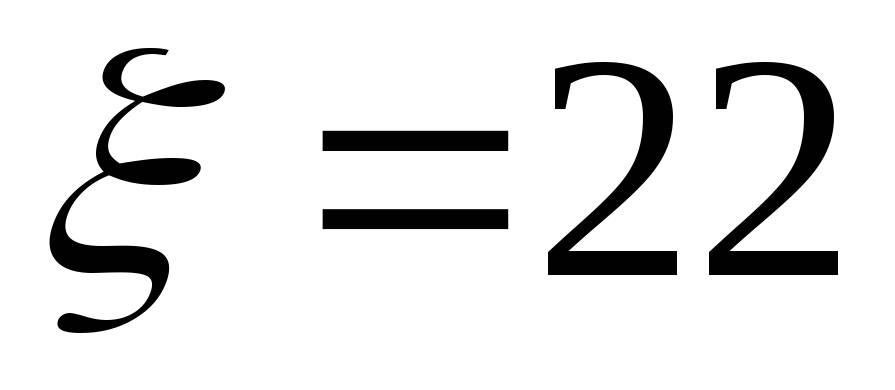 В)
и к.п.д.
В)
и к.п.д.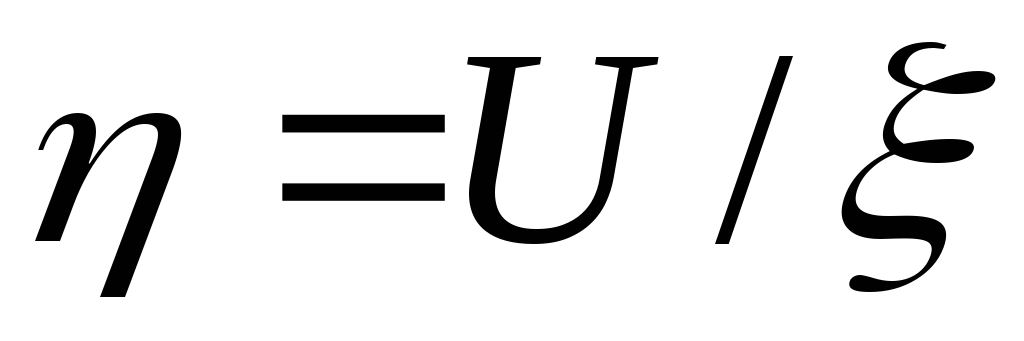 .
.Результаты измерений и вычислений занести в таблицу 1.
Таблица 1
|
№ п/п |
|
|
|
Р (Вт) |
рполн. (Вт) |
|
|
|
|
|
|
|
|
|
Построить графики зависимостей
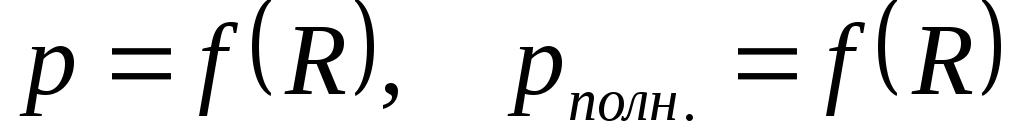 (на одном графике) и
(на одном графике) и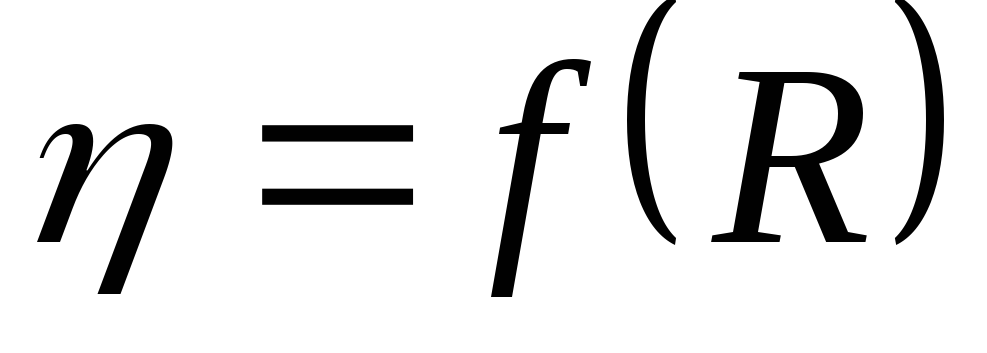 .
По максимуму полезной мощности и
значению к.п.д.
.
По максимуму полезной мощности и
значению к.п.д.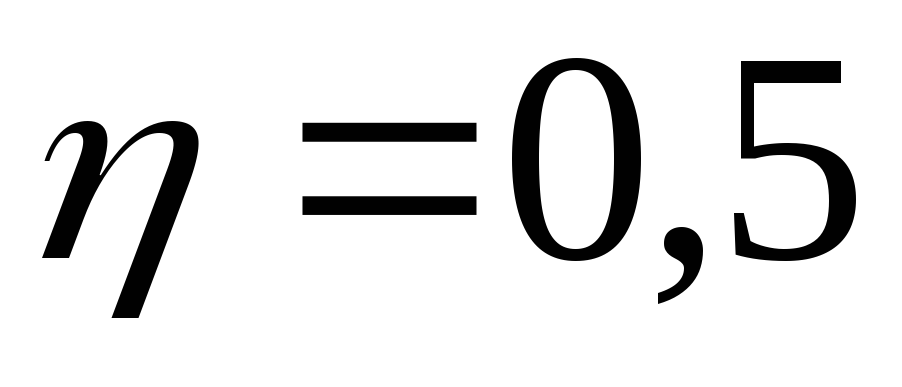 определить величину внутреннего
сопротивления источника
определить величину внутреннего
сопротивления источника .
.Провести обработку результатов на ЭВМ. Предварительно необходимо ознакомиться с инструкцией по обработке результатов физического практикума на ЭВМ.
4. ОБРАБОТКА РЕЗУЛЬТАТОВ
1. Рассчитать значения сопротивления нагрузки по формуле (7) и полезную мощность по формуле (6). Результаты расчетов свести в таблицу 1.
2.
Построить график зависимости
![]() .
Определить точкуR
= r.
.
Определить точкуR
= r.
3.
По формуле (8) определить ЭДС
![]() источника.
источника.
4.
Рассчитать полную мощность, развиваемую
источником для всех значений тока I
по формуле:
![]() .
.
5.
Рассчитать КПД источника по формуле
![]() .
.
6. Результаты расчетов п.п. 5,6 свести в таблицу 1.
7.
Построить графики зависимостей
![]() ,
,![]() ,
,![]() .
.
8.
Обработать результаты эксперимента на
ЭВМ. Сравнить
![]() и r
с рассчитанными в п.п. 3, 4.
и r
с рассчитанными в п.п. 3, 4.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА НА ЭВМ
Для ввода результатов эксперимента в компьютер необходимо обозначить у = U, х = I, данные представить в виде таблицы 2:
Таблица 2
-
х
у
1
2
.
.
.
10
Результаты
расчетов выдаются на дисплей в виде
двух чисел: а
= -r; b
=![]() .
.
