
Содержание
Источники погрешностей и их классификация . ...2
Приближенные числа, их запись и действия над ними...........3
Представление чисел ЭВМ и связанные с ним погрешности..7
Погрешность метода вычисления. Понятие об устойчивых алгоритмах...........................................................................….......13
Контрольные вопросы к лабораторной работе...................... ..16
Задания к лабораторной работе............................................... .17
Приложение 1............................................................................ .18
Приложение 2........................................................................... ...19
Список литературы.................................................................. ..23
1.1 Источники погрешностей и их классификация.
Анализ ошибок (погрешностей) в численном результате решения задачи должен являться непременной частью любого расчета, вне зависимости от того, проводятся ли вычисления “вручную” или при помощи ЭВМ. Погрешности решения задач могут возникать вследствие следующих причин:
1. Математическое описание задачи является неточным, в частности, неточно заданы исходные данные.
2. Применяемый метод решения задачи является приближенным, например, получение результата требует бесконечно большого числа арифметических операций (или неприемлемо большого).
3. Используемый инструмент для проведения вычислений сам вносит погрешности. Например, при выполнении вычислений на ЭВМ эта погрешность возникает при вводе данных в машину и при выполнении арифметических операций.
В соответствии с этой классификацией погрешности называются следующим образом: погрешность типа 1 - неустранимая погрешность, типа 2 - погрешность метода и типа 3 - вычислительная погрешность.
В настоящей работе мы будем заниматься оценкой погрешностей типа 1,2 и 3. Причем, погрешность типа 1 мы будем рассматривать только как погрешность задания исходных данных, поскольку задача оценки качества математической модели решается конкретной наукой, поставляющей данную модель.
1.2 Приближенные числа, их запись и действия над ними.
Пусть
х - точное (вообще говоря, неизвестное)
числовое значение некоторой величины;
х* - приближенное числовое значение этой
величины. Величина
 называется абсолютной погрешностью
приближенного числа х*, а величина
называется абсолютной погрешностью
приближенного числа х*, а величина соответственно называется его
относительной погрешностью. Когда
точное значение числа х неизвестно,
будем выбирать в качестве абсолютной
и относительной погрешностей величины
соответственно называется его
относительной погрешностью. Когда
точное значение числа х неизвестно,
будем выбирать в качестве абсолютной
и относительной погрешностей величины![]() и
и![]() ,
которые называются предельными
погрешностями, соответственно абсолютной
и относительной.
,
которые называются предельными
погрешностями, соответственно абсолютной
и относительной.
Наиболее аккуратный способ записи приближенного числа должен указывать соответствующую ему область неопределенности и, например, может иметь вид:
![]() ,
т.е.
,
т.е.
![]() ,
,
причем при выписывании абсолютной погрешности не рекомендуется удерживать более двух значащих цифр, т.е. нужно производить округление, оставив две значащие цифры.
При записи чисел в большую таблицу указанная выше форма записи будет громоздкой, потому можно договорится представлять приближенное число в таком виде, что по форме его записи можно судить о погрешности. Такую форму записи называют записью числа со всеми верными цифрами. Подробно обсудим ряд понятий, связанных с этим представлением чисел.
Рассмотрим представление (кодирование) чисел в десятичной системе счисления на конкретном примере:
![]()
Целое
число 123 имеет единицу разряда сотен,
двойку разряда десяток и тройку разряда
единиц. Любое число, в том числе и дробное,
представимо в виде суммы произведений
степеней десятки на цифры
{0,1,2,3,4,5,6,7,8,9}, причем числа, модуль которых
меньше 1 раскладываются по отрицательным
степеням десятки. В этом смысле любое
число
![]() можно представить в виде:
можно представить в виде:![]() где {
где {![]() }
- цифры числа до десятичной точки, {
}
- цифры числа до десятичной точки, {![]() }
- цифры числа после десятичной точки,
}
- цифры числа после десятичной точки,![]() - основание системы счисления. В нашем
случае
- основание системы счисления. В нашем
случае![]() ,
но совершенно очевидно, что
,
но совершенно очевидно, что![]() может быть любым целым числом с
естественным ограничением
может быть любым целым числом с
естественным ограничением![]() .
При записи числа
.
При записи числа![]() (мы сейчас отдельно не выделяем цифры
до и после десятичной точки), цифра
(мы сейчас отдельно не выделяем цифры
до и после десятичной точки), цифра![]() называется верной, если
называется верной, если![]() .
Число х*, записанное со всеми верными
цифрами, выглядит следующим образом:
.
Число х*, записанное со всеми верными
цифрами, выглядит следующим образом:
![]()
Иначе говоря, если число х* записано со всеми верными цифрами, то его погрешность не превосходит единицы его младшего разряда. Приведем примеры записи чисел с верными цифрами, если задана абсолютная погрешность числа
a)![]()
б)![]()
Пусть х* число записано со всеми верными цифрами, укажем его абсолютную погрешность:
a)
![]()
б)![]()
Чтобы показать, что абсолютная погрешность числа 314000 не превышает 103, (записать его со всеми верными цифрами), его предварительно нормализуют (т.е. записывают в виде 0.314000106) и далее поступают аналогично рассмотренному выше.
При выполнении арифметических операций над приближенными числами необходимо уметь оценивать погрешности результата. Приведем правила оценки погрешности для арифметических операций:
a)
сложение и вычитание:
![]()
б) умножение и деление:
![]()
Эти правила можно сформулировать в следующем виде. При сложении и вычитании приближенных чисел предельная абсолютная погрешность результата равна сумме абсолютных погрешностей, а при умножении и делении предельная относительная погрешность результата равна сумме относительных погрешностей.
Приведем
также правило приближенной оценки
погрешности значения функции
![]() если заданы погрешности
если заданы погрешности![]()
![]()
Пример №1.
Радиус
круга измерен с точностью
![]() Оценить погрешность расчета площади
круга.
Оценить погрешность расчета площади
круга.
Решение:
Площадь
круга
![]() Абсолютную погрешность в вычислении
площади определим по формуле
Абсолютную погрешность в вычислении
площади определим по формуле![]() и относительную
и относительную
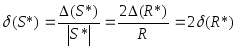
Иногда
приходиться решать обратную задачу,
т.е. по заданной погрешности
![]() функции
функции![]() определить
погрешность x*. Как нетрудно видеть, эта
задача легко решается на основе
приведенной выше формулы.
определить
погрешность x*. Как нетрудно видеть, эта
задача легко решается на основе
приведенной выше формулы.
Пример №2.
С
какой погрешностью следует измерять
радиус круга, чтобы погрешности вычисления
площади не превзошла
![]() .
.
Решение:
В
предыдущем примере мы имели оценку
погрешности вычисления площади круга
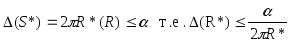 .
.
Задачи для самостоятельного решения
Написать число p и число pn в p-ичной системе счисления.
Составить таблицу умножения и сложения для двоичной системы счисления.
Какие из рациональных чисел могут быть точно представлены конечными p-ичными числами.
Указать какой-нибудь алгоритм деления p-ичных чисел.
Записать числа
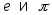
 с
тремя верными цифрами и определить их
предельные абсолютные и относительные
погрешности.
с
тремя верными цифрами и определить их
предельные абсолютные и относительные
погрешности.Сторона квадрата приблизительно 1 м. С какой точностью ее надо измерить, чтобы погрешность определяемой площади составила 1 см2.
Корни уравнения
 , нужно получить с четырьмя верными
цифрами. С каким числом цифр необходимо
взять свободный член уравнения
, нужно получить с четырьмя верными
цифрами. С каким числом цифр необходимо
взять свободный член уравненияС какой точностью необходимо измерить диаметр шара
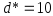 см, чтобы погрешность вычисления объема
составила 0,1 см3.
см, чтобы погрешность вычисления объема
составила 0,1 см3.Оценить пределы применимости формулы линейной оценки погрешности.
1.3 Представление чисел в ЭВМ и связанные с ним погрешности.
Современные ЭВМ оперируют с числами, представленными в одной из приведенных ниже форм.
а) Форма с фиксированной запятой.
Эта форма используется для представления данных диапазон изменения, которых, заранее известен. Таковыми, могут являться денежные величины 128 руб. 31 коп. (запятая у числа 12831 фиксирована на втором месте от левого края числа). В этой форме обычно представляются данные целого типа, хотя в машинном представлении все числа имеют модуль меньше единицы, число знаков после запятой фиксировано и число имеет следующий вид:
![]() (3.1)
(3.1)
Здесь
![]() - основание системы счисления,
- основание системы счисления,
![]() -
целые, в пределах
-
целые, в пределах
![]() ,
t - длина разрядной сетки. Из формулы
(3.1) очевидно, что предельная абсолютная
погрешность представления числа есть
,
t - длина разрядной сетки. Из формулы
(3.1) очевидно, что предельная абсолютная
погрешность представления числа есть![]() ,
если число имеет более чем
,
если число имеет более чем![]() значащих цифр, и
значащих цифр, и![]() в противном случае. Числа меньше, чем
в противном случае. Числа меньше, чем![]() представлены как ноль. При операциях
над числами
представлены как ноль. При операциях
над числами![]() могут появиться числа
могут появиться числа![]() ,
в этом случае (в зависимости от конкретной
реализации арифметики с фиксированной
запятой) может произойти аварийный
останов машины, обнуление результата
или число будет переписано в другой
форме.
,
в этом случае (в зависимости от конкретной
реализации арифметики с фиксированной
запятой) может произойти аварийный
останов машины, обнуление результата
или число будет переписано в другой
форме.
б) Форма с плавающей запятой.
Эта
форма используется для представления
данных диапазон изменения, которых
заранее неизвестен. Она является наиболее
распространенной формой представления
чисел в ЭВМ, при проведении научных
расчетов. При этом число, х представлено
в виде числа с фиксированной запятой
умноженного на масштабный множитель
![]()
![]() (3.2)
(3.2)
где
![]() - основание системы счисления;
- основание системы счисления;![]() - целые, в пределах
- целые, в пределах![]() ,
t - длина разрядной сетки. Наиболее
употребительны
,
t - длина разрядной сетки. Наиболее
употребительны![]() 2,
10, 16. Типичные значения t=8, 16, 32, 64 и наиболее
распространен интервал показателя
масштабного множителя
2,
10, 16. Типичные значения t=8, 16, 32, 64 и наиболее
распространен интервал показателя
масштабного множителя![]() .
Число
.
Число![]() обычно называют показателем, а (
обычно называют показателем, а (![]() )-
мантиссой числа х (она, как правило,
задается в нормализованной форме т.е.
)-
мантиссой числа х (она, как правило,
задается в нормализованной форме т.е.![]() ).
Множество чисел с плавающей запятой,
которое мы будем обозначать F,
характеризуется следующими параметрами
:
).
Множество чисел с плавающей запятой,
которое мы будем обозначать F,
характеризуется следующими параметрами
:![]() и
интервалом значений показателя
и
интервалом значений показателя![]() Множество F чисел очевидно не является
бесконечным, Эти числа расположены
неравномерно, равномерность имеет место
только при фиксированном показателе
Множество F чисел очевидно не является
бесконечным, Эти числа расположены
неравномерно, равномерность имеет место
только при фиксированном показателе![]() .
Операции сложения и умножения чисел на
этом множестве очевидно коммутативны,
но не ассоциативны и не дистрибутивны.
Поскольку эти законы имеют основополагающее
значение для математического анализа,
то учет всех особенностей вычислений
на данном множестве чисел достаточно
сложен.
.
Операции сложения и умножения чисел на
этом множестве очевидно коммутативны,
но не ассоциативны и не дистрибутивны.
Поскольку эти законы имеют основополагающее
значение для математического анализа,
то учет всех особенностей вычислений
на данном множестве чисел достаточно
сложен.
Рассмотрим
ряд простых примеров иллюстрирующих
возникновение погрешностей при операциях
с плавающей запятой. Операции сложения
и умножения, алгоритмы которых мы здесь
приведем, могут в деталях отличаться
от действительных, но эти различия, как
правило, можно игнорировать, говоря об
основных проблемах появления ошибок
связанных с вычислениями на ЭВМ. Из
формулы (3.2) следует, что предельная
относительная погрешность
![]() представления числа х, не большие чем
представления числа х, не большие чем![]() ,
т.е. корректная форма записи приближенного
числа х:
,
т.е. корректная форма записи приближенного
числа х:
![]() .
.
При сложении и вычитании чисел с плавающей запятой предварительно выравниваются порядки чисел. Это означает, что мантисса меньшего по абсолютной величине числа сдвигается вправо на столько разрядов, сколько необходимо, чтобы порядки стали одинаковыми, а затем производится сложение мантисс чисел. При умножении и делении операции с мантиссами чисел и их порядками производятся независимо.
Рассмотрим
пример сложения двух чисел на гипотетической
машине, в которой параметры арифметики
с плавающей запятой таковы:
![]() Пусть имеем два числа:
Пусть имеем два числа:
![]()
После выравнивания порядков получится следующий результат:
![]()
Во
втором числе цифры 2, 9 не могут быть
представлены в нашем множестве F и
поэтому будут утрачены. В результате
это скажется на абсолютной погрешности
суммы, а относительная погрешность
суммы по прежнему будет оцениваться
величиной
![]() Более точное значение относительной
погрешности Е (машинное эпсилон), можно
определить в результате выполнения
программы, если мы определим Е, как
наименьшее число с плавающей запятой,
для которого еще имеет место неравенство:
Более точное значение относительной
погрешности Е (машинное эпсилон), можно
определить в результате выполнения
программы, если мы определим Е, как
наименьшее число с плавающей запятой,
для которого еще имеет место неравенство:
![]()
Фрагмент такой программы, которая дает значение Е, с точностью до некоторого множителя, приведен в приложении 1. Там же приведены программы, по которым можно определить диапазон показателя порядка.
Задачи для самостоятельного решения
Привести примеры физических устройств, имеющих p устойчивых состояний.
Предложить какой-либо способ представления чисел отличный от фиксированной и плавающей запятой. Как при этом выполняются операции над числами.
Имеет ли место неоднозначность представления каких-либо чисел в форме с фиксированной и плавающей запятой?
Будет ли операция умножения ассоциативной при каком-либо способе округления?
Будет ли операция сложения ассоциативной при каком-либо способе округления?
Можно ли выбором способа округления добиться выполнения закона дистрибутивности?
Привести примеры возможных пар алгебраических операций на ЭВМ, для которых выполняются законы коммутативности, ассоциативности и дистрибутивности.
Для каких чисел на ЭВМ операции сложения и умножения с плавающей запятой выполняются абсолютно точно?
Выяснить, как устроено округление на Вашей ЭВМ?
Хорошо известно, что ряд для
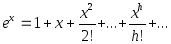 хорошо представляет экспоненту.
Предлагается найти (составив программу)
значение
хорошо представляет экспоненту.
Предлагается найти (составив программу)
значение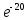 и сравнить полученное значение со
значением, даваемым встроенной функцией.
и сравнить полученное значение со
значением, даваемым встроенной функцией.Найти корни квадратного уравнения
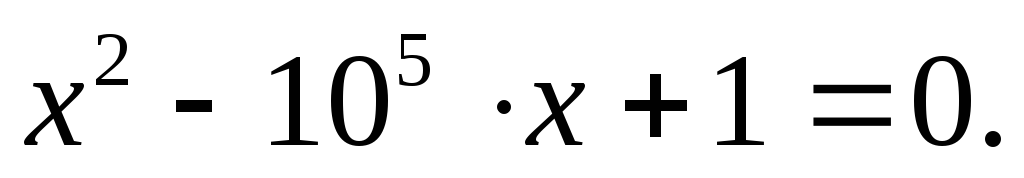 Ответ проверить подстановкой решений
в уравнение. Объяснить полученный
результат.
Ответ проверить подстановкой решений
в уравнение. Объяснить полученный
результат.Для функции Ф(х)=
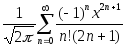 (т.н. интеграл вероятности или функция
Лапласа), вычислите ее значения для
х=0.5, 1.0, 5.0, 10.0 и сравните полученные
значения с данными таблицы.
(т.н. интеграл вероятности или функция
Лапласа), вычислите ее значения для
х=0.5, 1.0, 5.0, 10.0 и сравните полученные
значения с данными таблицы.Будет ли десятичное число 0.1 точно представимо в вашей машине? Каково ближайшее число с плавающей точкой среди чисел меньших 0.1?
Вычислите сумму ряда из задачи №12 для х=0, шаг 0.1 до 1 с ошибкой, не превышающей
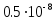 .
.Вычислить сумму ряда
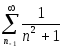 ,
точностью 10-7.
,
точностью 10-7.Дан круговой сектор следующих размеров: АВ=2640; АСВ=2640.5. Найти СМ, с точностью до 5 значащих цифр.
С



 А В
А В
М
О
Составив программу, определите параметры арифметики с плавающей запятой для Вашей машины (см. приложение 1).
Определить величину машинного нуля. (максимального числа, представимого как ноль на ЭВМ).
Построить графики относительной и абсолютной погрешностей, представления чисел с фиксированной и плавающей запятой, как функцию величины числа.
Квадратное уравнение
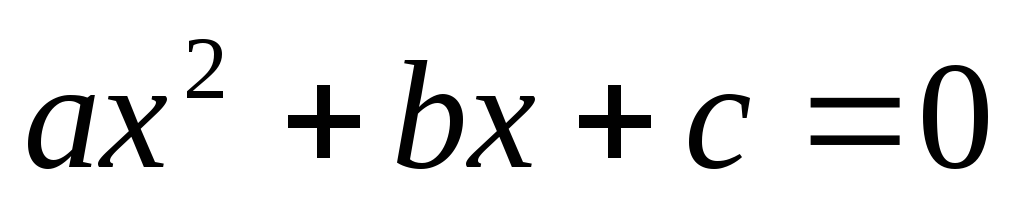 имеет два решения, даваемые формулой
имеет два решения, даваемые формулой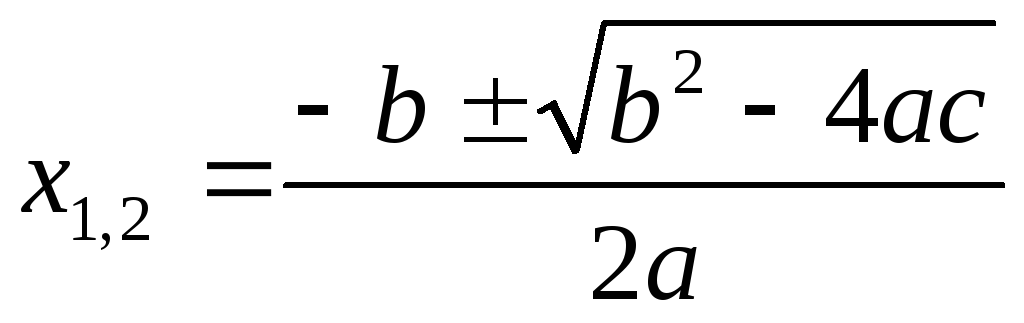 .
Пусть арифметика с плавающей запятой
задана параметрами:
.
Пусть арифметика с плавающей запятой
задана параметрами: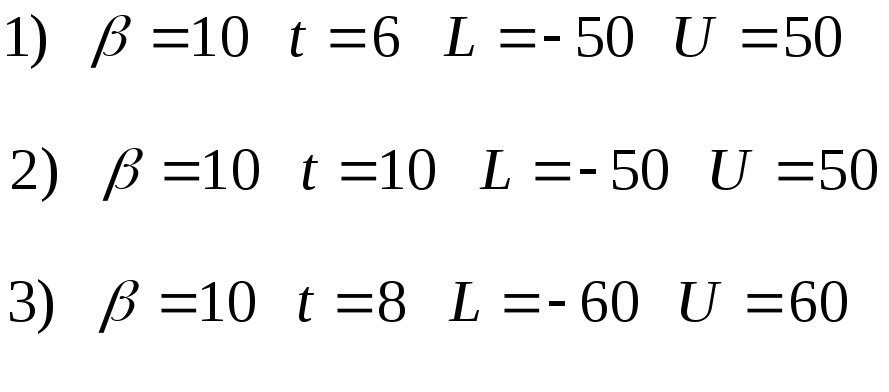 ,
получить решения, для случаев:
,
получить решения, для случаев:

![]() ,
,
и произвести оценку погрешности.
Рассмотрим трехзначную десятичную плавающую систему с усечением числа, имеющего вид
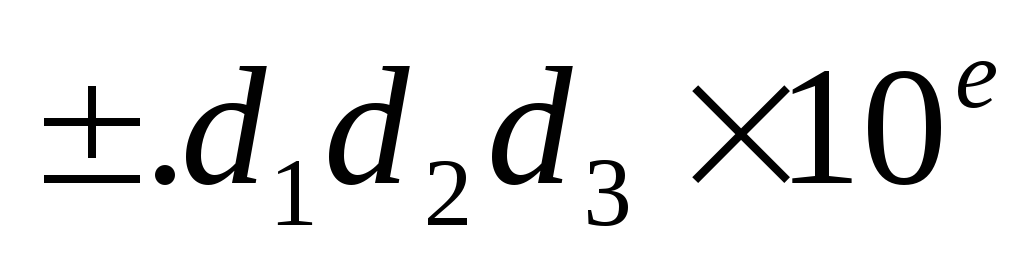 ,
где
,
где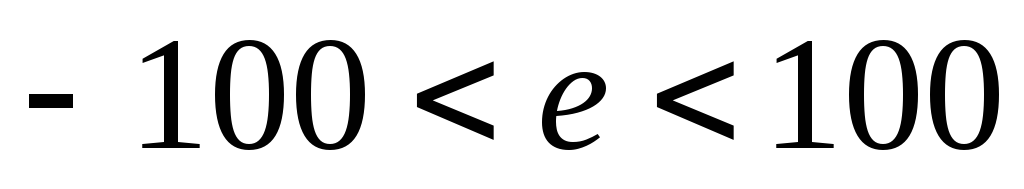 и
и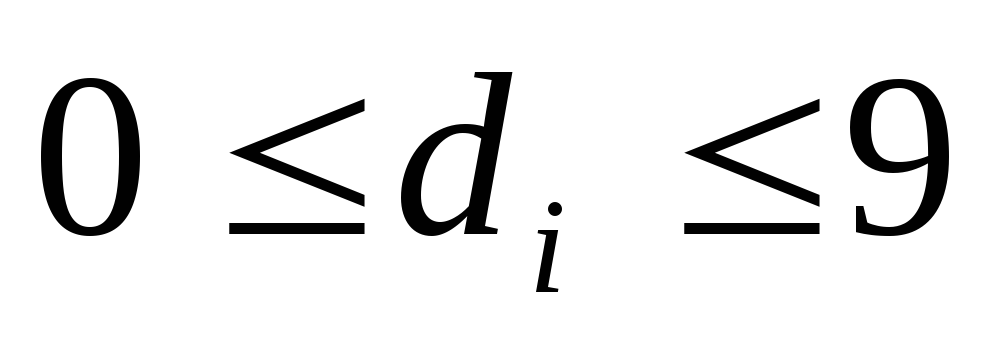 ,
причем
,
причем ,
для
,
для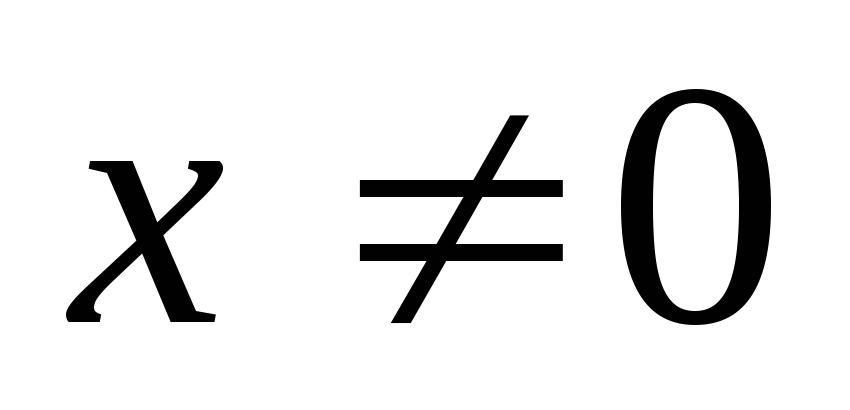 .
Число нуль имеет единственное
представление
.
Число нуль имеет единственное
представление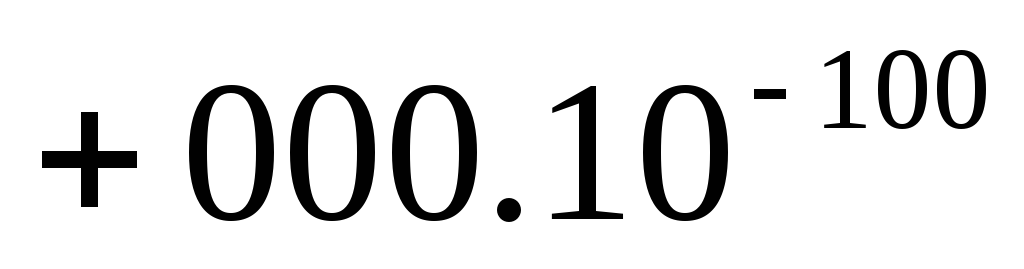 .
Посредством
.
Посредством и
и будем обозначать операции сложения и
умножения. Для всех чисел величины
будем обозначать операции сложения и
умножения. Для всех чисел величины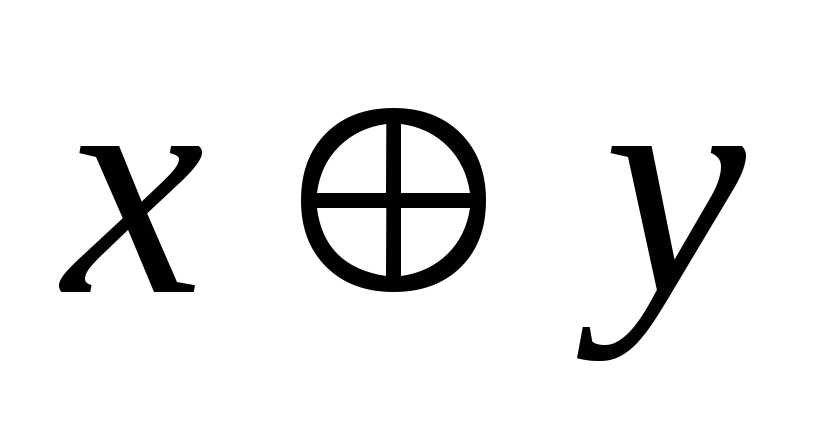 и
и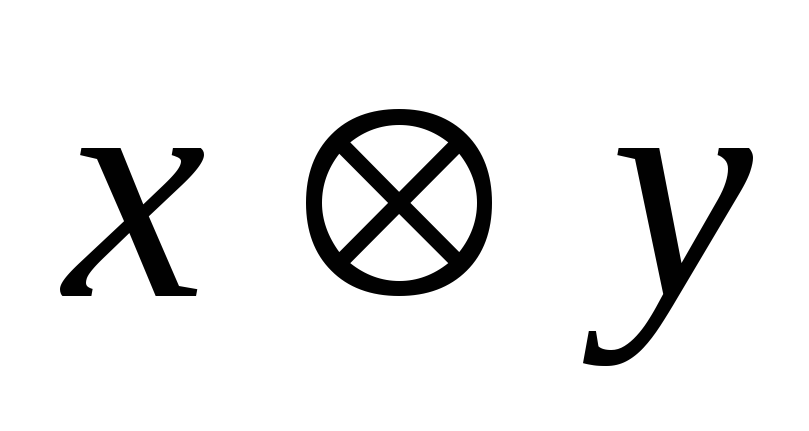 определяются, как числа с плавающей
запятой, ближайшие к
определяются, как числа с плавающей
запятой, ближайшие к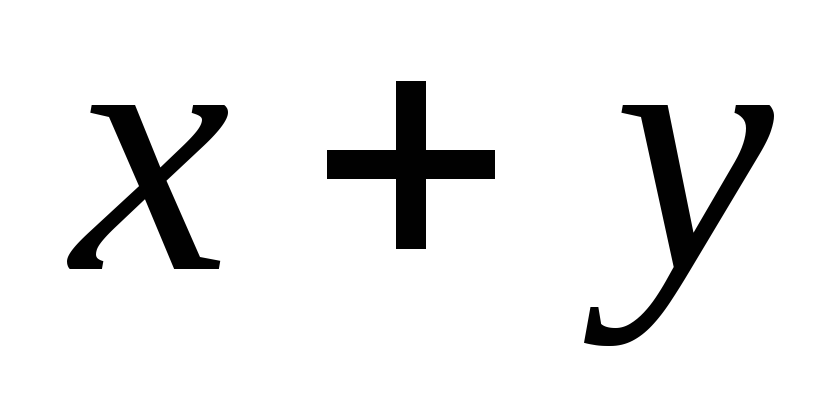 и
и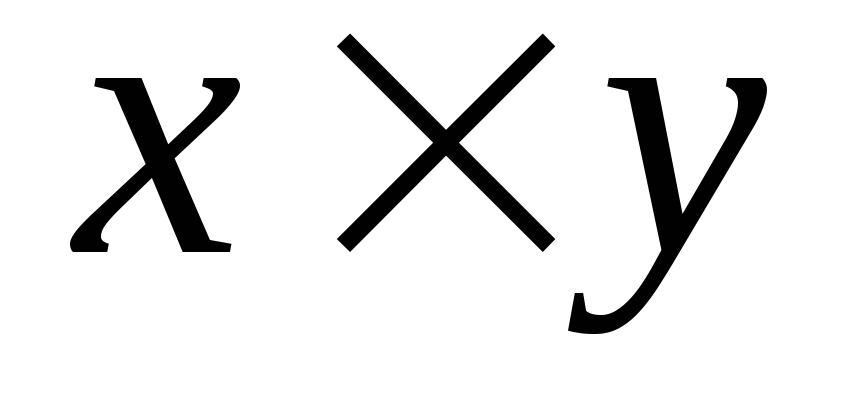 ,
но не превосходящие их по модулю.
,
но не превосходящие их по модулю.
а) Сколько различных чисел могут быть представлены абсолютно точно?
б) Найдите примеры чисел, показывающие, что нижеследующие равенства, вообще говоря, неверны, даже если результат принадлежит множеству точно представимых чисел
![]()
в)
Найдите пример, в котором сумма
![]() имеет относительную ошибку, по меньшей
мере, 50%.
имеет относительную ошибку, по меньшей
мере, 50%.
1.4 Погрешность метода вычисления. Понятие об устойчивых алгоритмах.
Для некоторых задач вычислительного характера удовлетворительную точность, при решении ее на ЭВМ, нельзя получить никаким алгоритмом, потому что задача чувствительна к малым ошибкам, допущенным в представлении данных и возникающим при выполнении арифметических операций. Эти задачи называются неустойчивыми (некорретными). Задачи такого типа в настоящей лабораторной работе мы рассматривать не будем, это самостоятельная и обширная тема, а будем рассматривать только те задачи, в которых путем изменения алгоритма решения можно избежать накапливания погрешностей.
Будем
называть алгоритм решения задачи
устойчивым, если при его реализации
погрешности вычисления не накапливаются,
с ростом объема вычмслений. Приведем
пример неустойчивого алгоритма.
Рассмотрим расчет значений Еn
по рекуррентной
формуле
![]() .
Эта формула возникает при вычислении
интеграла
.
Эта формула возникает при вычислении
интеграла![]() .
Как нетрудно видеть, величина
.
Как нетрудно видеть, величина![]() Вычисления, проведённые на ЭВМ с
Вычисления, проведённые на ЭВМ с![]() дают результаты из которых видно, что
величина
дают результаты из которых видно, что
величина![]() становится
отрицательной, уже для n=20.
становится
отрицательной, уже для n=20.![]() Заметим,
что единственная ошибка округления,
сделанная в приведенных вычислениях,
связана с ошибками представления
Заметим,
что единственная ошибка округления,
сделанная в приведенных вычислениях,
связана с ошибками представления![]() ,
предполагая, что арифметические операции
выполняются точно. Причину катастрофического
роста погрешности вычисления
,
предполагая, что арифметические операции
выполняются точно. Причину катастрофического
роста погрешности вычисления![]() легко установить, заметив, что
первоначальная ошибка в
легко установить, заметив, что
первоначальная ошибка в![]() при вычислении
при вычислении![]() умножается на -2,
умножается на -2,![]() на -3 и т.д., т.е. при вычислении
на -3 и т.д., т.е. при вычислении![]() эта ошибка умножается на огромное число
20!, и тем самым, ошибка в вычислении
эта ошибка умножается на огромное число
20!, и тем самым, ошибка в вычислении![]() составит
составит![]() Очевидно, что приведенный алгоритм
является неустойчивым. Рассмотрим,
каким образом его можно сделать
устойчивым. Для этого перепишем
рекуррентную формулу в виде:
Очевидно, что приведенный алгоритм
является неустойчивым. Рассмотрим,
каким образом его можно сделать
устойчивым. Для этого перепишем
рекуррентную формулу в виде:
![]()
Поскольку
последовательность
![]() является монотонно убывающей, то в
качестве
является монотонно убывающей, то в
качестве![]() можно взять значение равное нулю, что
конечно вносит погрешность в результат
вычисления
можно взять значение равное нулю, что
конечно вносит погрешность в результат
вычисления![]() ,
но эта погрешность будет уменьшаться
в результате деления на n и при вычислении
,
но эта погрешность будет уменьшаться
в результате деления на n и при вычислении![]() величина ошибки, связанной с неточным
заданием
величина ошибки, связанной с неточным
заданием![]() , станет исчезающей малой и приведенный
алгоритм будет являться устойчивым.
, станет исчезающей малой и приведенный
алгоритм будет являться устойчивым.
