Министерство образования и науки Российской Федерации

Читинский институт (филиал)

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«БАЙКАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЭКОНОМИКИ И ПРАВА»

Кафедра математики

Контрольная работа по дисциплине «Математический анализ»

Часть 5 «функции многих переменных»

для студентов 1-го курса по направлению подготовки 080100 Экономика:

080100.01 – Экономика предприятия и предпринимательская деятельность

080100.02 – Мировая экономика

080100.03 – Финансы и кредит

080100.04 – Бухгалтерский учет, анализ и аудит

Чита-2012

Печатается по решению учебно-методической комиссии ЧИ БГУЭП

Протокол № ______ от __ ________ 2012г.

Составитель: к.ф.-м.н., профессор кафедры математики Лесков Б.П.

Рекомендовано к печати кафедрой математики

Протокол заседания № _2_ от_18 октября_ 2012г.

Задания для самостоятельной работы

1. Для функции z =ƒ(x‚y) указать область ее определения и область ее значений. Построить линии уровня поверхности, определенной этой функцией.

1.	z = x2 - y2	16.	z = 16x2 – 25y2
2.		17.	z = x2 – 2x + y2 +2y
3.		18.	z = 5x – 3y + 2
4.	z = x - y2	19.	z = x2 + 4x – y2
5.	z = x2 + y	20.	z = 4x2 + 16x – y2 – 8y
6.		21.	z = x + y2
7.	z = x2 - 3y2 + 5	22.
8.	z = x2 + 2x + y2 - 2y	23.	z = 49x2 + 9y2
9.	z = 16x2 + 25y2	24.	z = x2 – y2 – 4y
10.		25.
11.	z = 25x2 - 16y2	26.
12.		27.	z = 4x2 – y2 – 8y
13.	z = x - 3y - 8	28.
14.	z = x - 9y2	29.	z = x2 + 2x – 4y2
15.	z = 2x2 – y	30.	z = 2x2 – 4y2 + 5

2. Найти частные производные и полные дифференциалы первого порядка функции

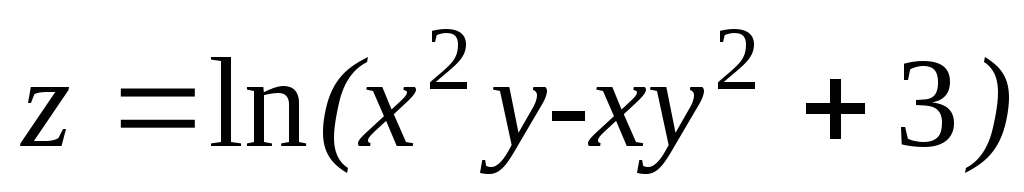
1.		2.
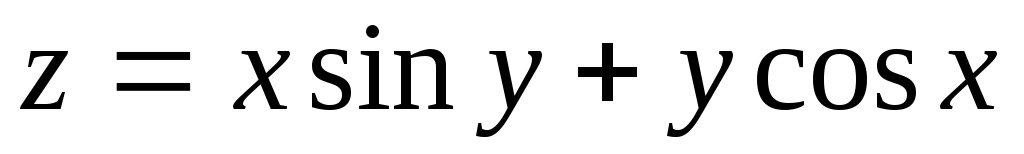
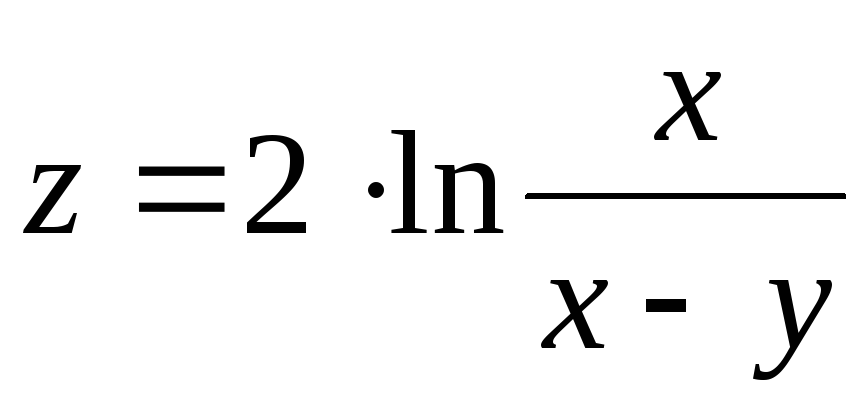
3.		4.
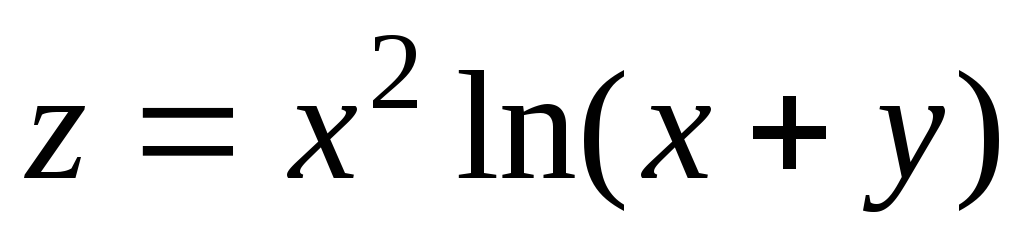
5.		6.
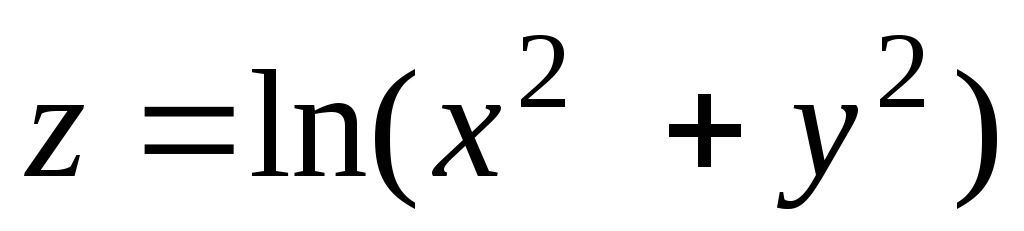
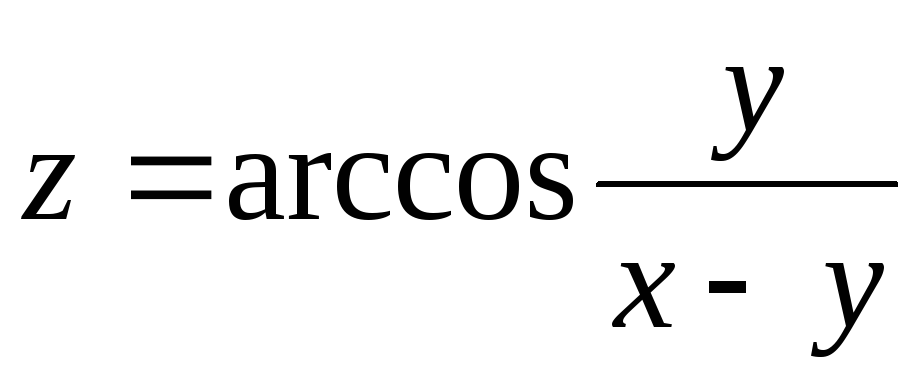
7.		8.
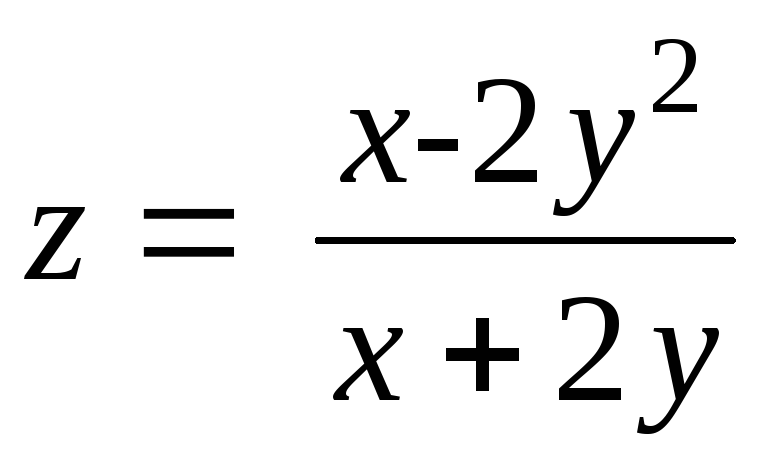
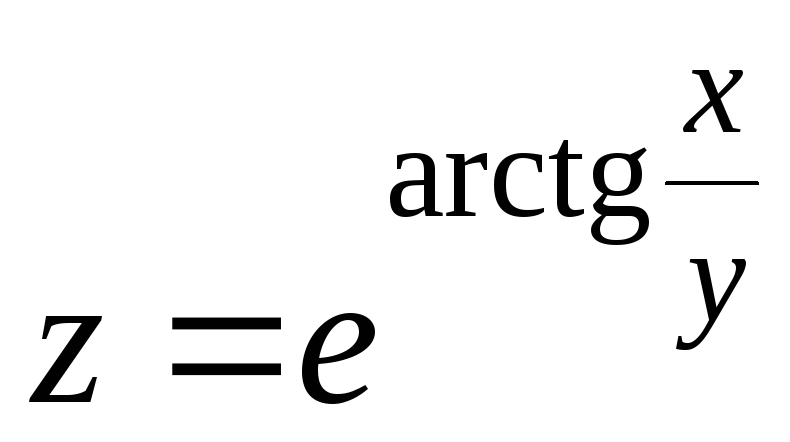
9.		10.
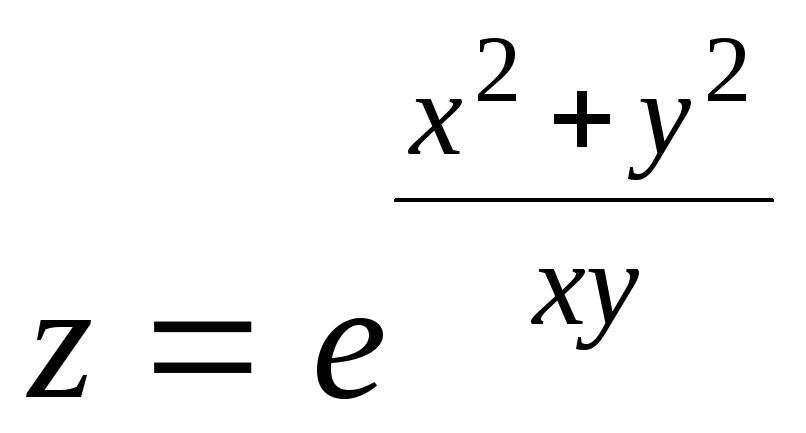
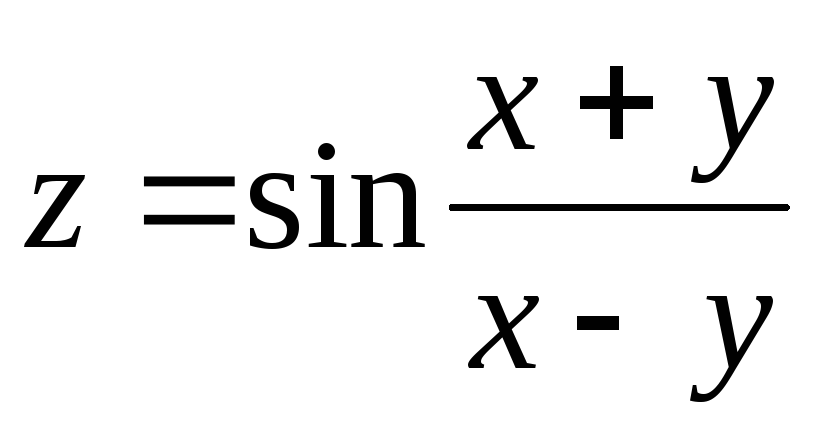
11.		12.
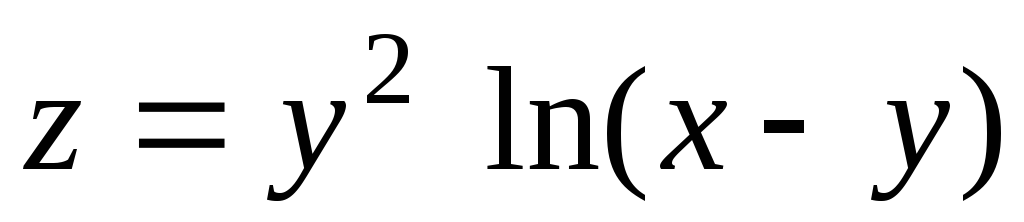
13.		14.
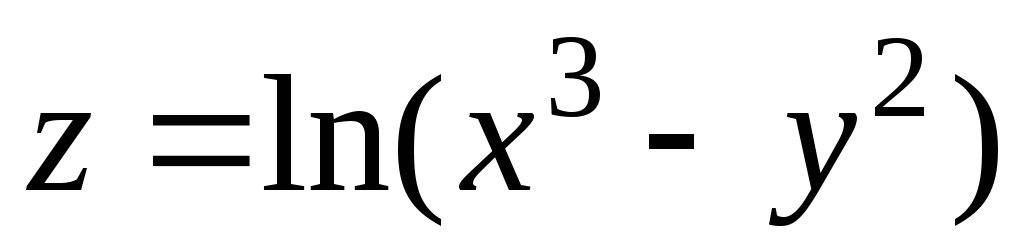
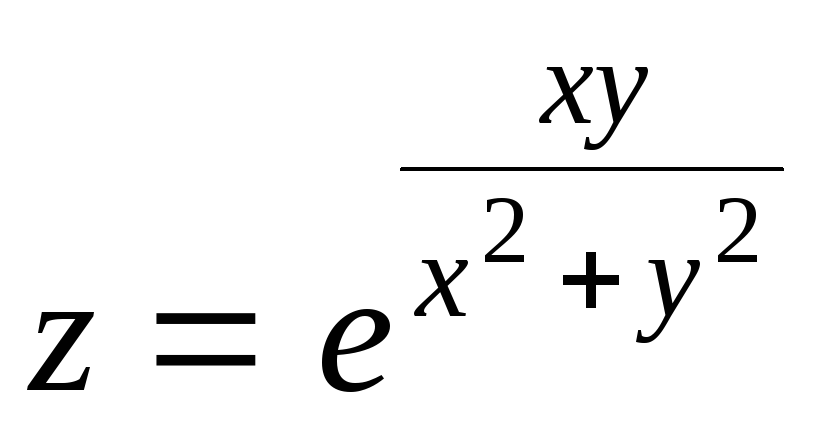
15.		16.
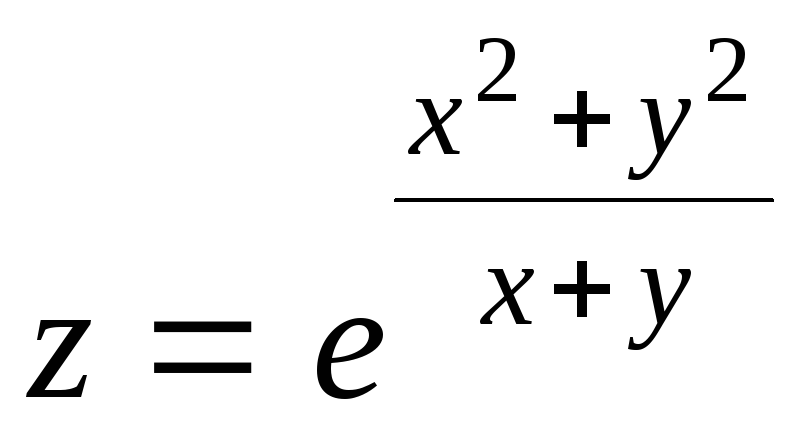
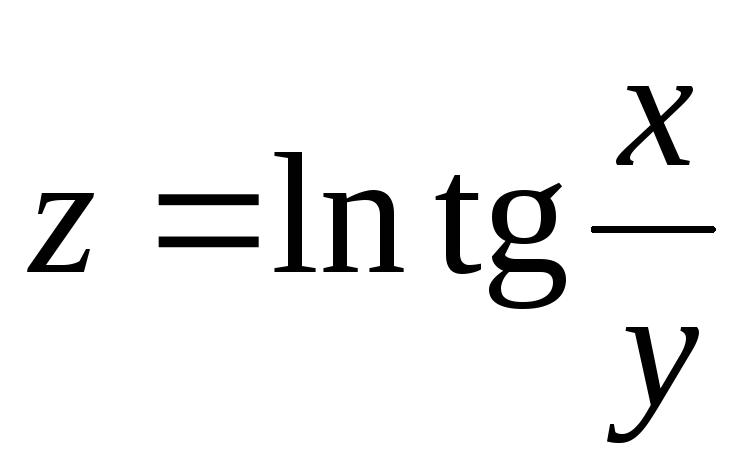
17.		18.
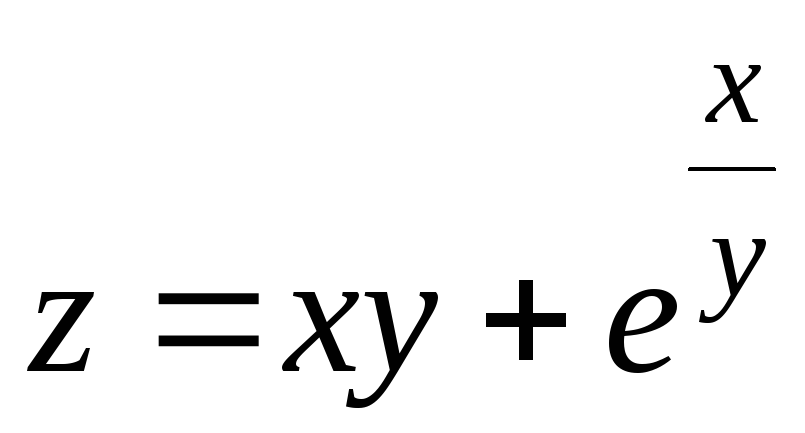
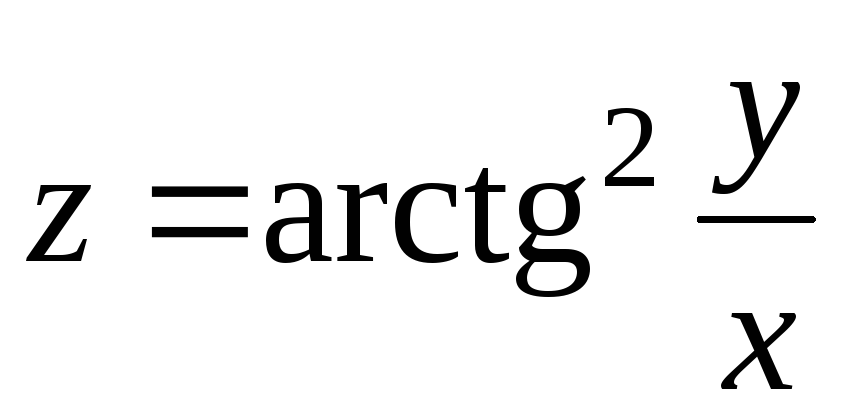
19.		20.
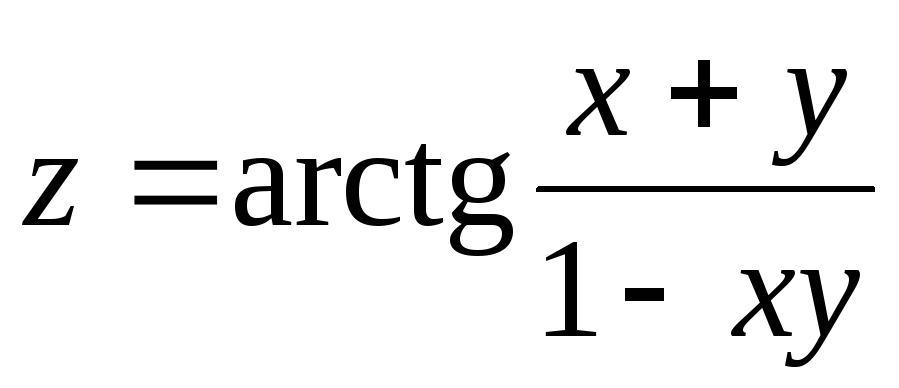
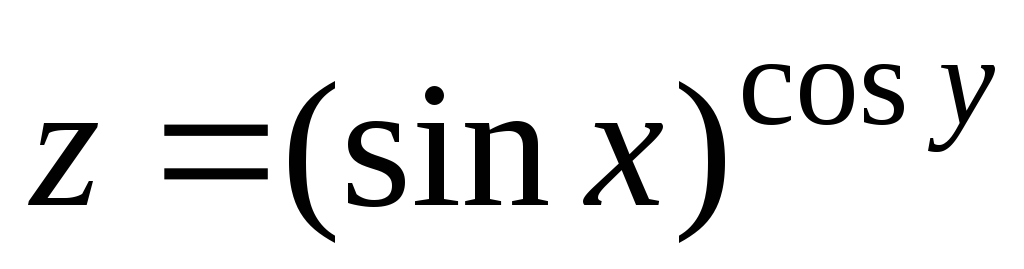
21.		22.
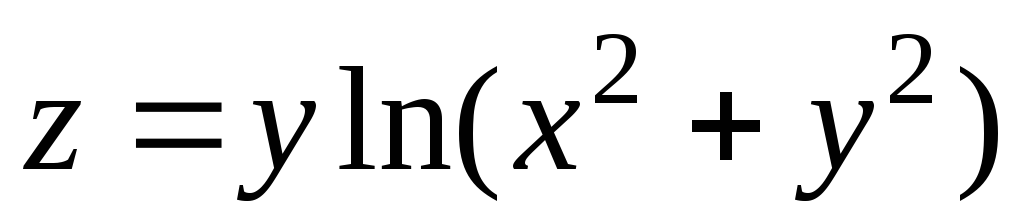
23.		24.
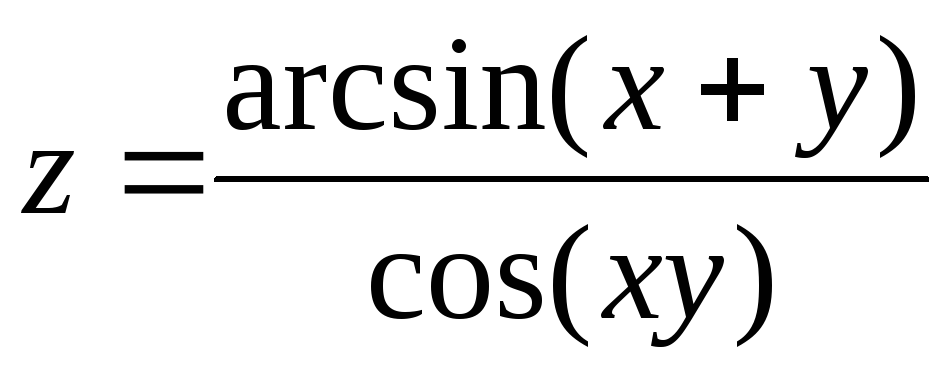
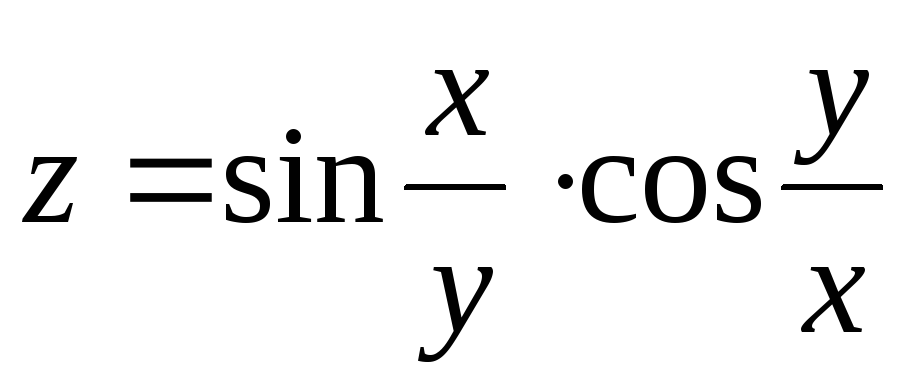
25.		26.
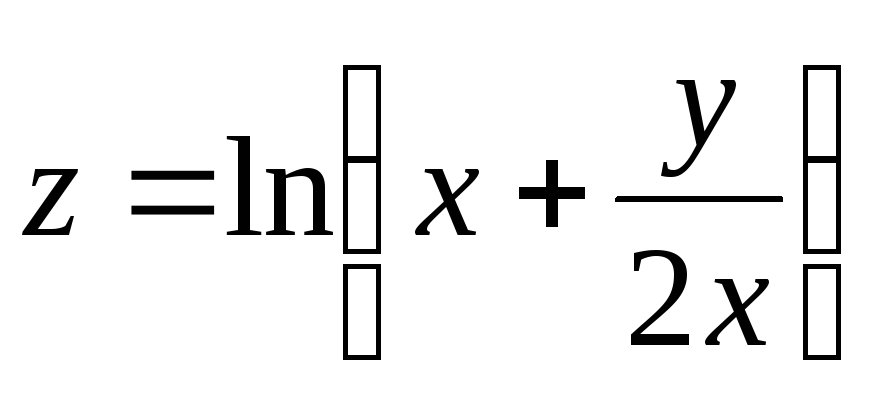
27.		28.
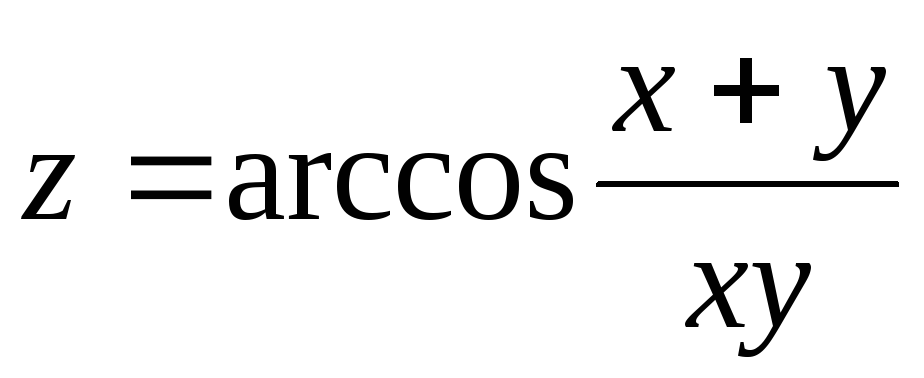
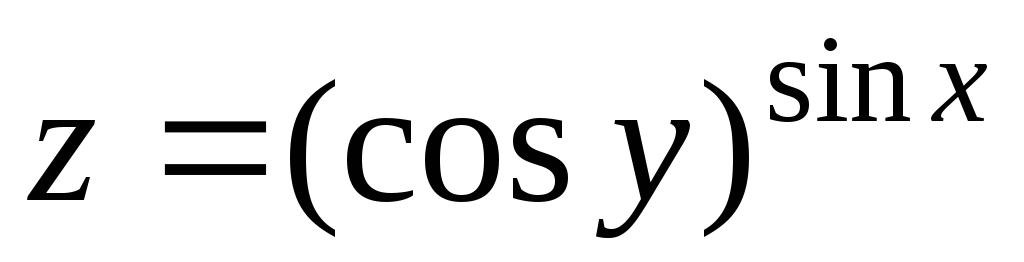
29.		30.