
kletenik_doc / kletenik_o4
.docОТВЕТЫ (Глава 4)
385. 1) x2
— y2
= 9; 2) (x
— 2)2
+ (y
+ 3)2
= 49; 3) (x
– 6)2
+ (y
+ 8)2
= 100 4) (x
+ 1)2
+ (y
– 2)2
= 25; 5) (x
– 1)2
+ (y
– 4)2
=8; 6) х2
+ у2
= 16;
7) (x
— 1)2
+ (y
+ 1)2
= 4; 8) (x
— 2)2
+ (y
— 4)2 =
10; 9) (x
—l)2
+ y2
= 1; 10) (x
—2)2
+ (y
— 1)2
= 25. 386.
(x
— 3)2
+ (y
+ 1)2
= 38. 387.
(x
— 4)2
+ (y
+ 1)2
= 5 и (x
— 2)2
+ (y
— 3)2
= 5. 388.
(x
+ 2)2
+ (y
+ 1)2
= 20. 389.
(x
— 5)2
+ (у
+ 2)2
= 20 и (x
—
![]() )2
+ (y
—
)2
+ (y
—
![]() )2
= 20. 390.
(x
— 1)2
+ (у +
2) = 16. 391.
(x +
6)2
+ (y
— 3)2
= 50 и (y
— 29)2
+ (у +
2)2
= 800. 392.
(х —
2)3
+ (y
— 1)2
=5 и (x
—
)2
= 20. 390.
(x
— 1)2
+ (у +
2) = 16. 391.
(x +
6)2
+ (y
— 3)2
= 50 и (y
— 29)2
+ (у +
2)2
= 800. 392.
(х —
2)3
+ (y
— 1)2
=5 и (x
—
![]() )2
+ (y
+
)2
+ (y
+
![]() )2
=
)2
=
![]() . 393.
(x
— 2)2
+ (y
— 1)2
=
. 393.
(x
— 2)2
+ (y
— 1)2
=
![]() ,
(x
+ 8)2
+ (y
+ 7)2
=
,
(x
+ 8)2
+ (y
+ 7)2
=
![]() .
394.
(х — 2)2 +
(y
— 1)2
= 25 и (x
+
.
394.
(х — 2)2 +
(y
— 1)2
= 25 и (x
+
![]() )
+ (y
—
)
+ (y
—
![]() )2
= (
)2
= (![]() )2
. 395.
(x
+
)2
. 395.
(x
+
![]() )2
+ (y
+
)2
+ (y
+
![]() )
= 1 и (x
—
)
= 1 и (x
—
![]() )2
+ (y
—
)2
+ (y
—
![]() )2
= 1. 396.
(х —
5)2 +
у2
= 16,
(x
+ 15)2 +
y2
= 256, (x
—
)2
= 1. 396.
(х —
5)2 +
у2
= 16,
(x
+ 15)2 +
y2
= 256, (x
—
![]() )
+ (y
—
)
+ (y
—
![]() )2
= (
)2
= (![]() )2
и (x
—
)2
и (x
—
![]() )2
+ (y
+
)2
+ (y
+
![]() )2
= (
)2
= (![]() )2.
397. Уравнения
1), 2), 4), 5), 8) и 10) определяют окружности;
1) С(5;
—2), R
= 5; 2) С(—
2; 0), R
= 8; 3) уравнение определяет единственную
точку (5;—2); 4) С(0;
5), R
=
)2.
397. Уравнения
1), 2), 4), 5), 8) и 10) определяют окружности;
1) С(5;
—2), R
= 5; 2) С(—
2; 0), R
= 8; 3) уравнение определяет единственную
точку (5;—2); 4) С(0;
5), R
=
![]() ;
5) С
(1; — 2), R
= 5;
;
5) С
(1; — 2), R
= 5;
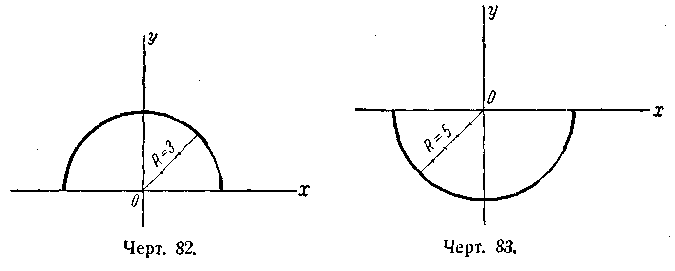
6)уравнение
не определяет никакого геометрического
образа на плоскости; 7) уравнение
определяет единственную точку (—2; 1);
8) С(
—
![]() ;
0), R
=
;
0), R
=
![]() ;
9) уравнение не определяет никакого
геометрического образа на плоскости;
10) C(0;
—
;
9) уравнение не определяет никакого
геометрического образа на плоскости;
10) C(0;
—![]() )
R
=
)
R
=
![]() .
398.
Полуокружность радиуса R
= 3 с центром в начале
координат, расположенная в верхней
полуплоскости (черт. 82); 2) полуокружность
радиуса R
= 5 с центром в начале координат,
расположенная в нижней полуплоскости
(черт. 83); 3) полуокружность радиуса R
= 2 с центром в начале координат,
расположенная в левой полуплоскости
(черт. 84); 4) полуокружность радиуса R
= 4 с центром в начале
координат, расположенная в правой
полуплоскости (черт. 85);
.
398.
Полуокружность радиуса R
= 3 с центром в начале
координат, расположенная в верхней
полуплоскости (черт. 82); 2) полуокружность
радиуса R
= 5 с центром в начале координат,
расположенная в нижней полуплоскости
(черт. 83); 3) полуокружность радиуса R
= 2 с центром в начале координат,
расположенная в левой полуплоскости
(черт. 84); 4) полуокружность радиуса R
= 4 с центром в начале
координат, расположенная в правой
полуплоскости (черт. 85);

5) полуокружность радиуса R = 8 с центром С (0; 15), расположенная над прямой у — 15 = 0
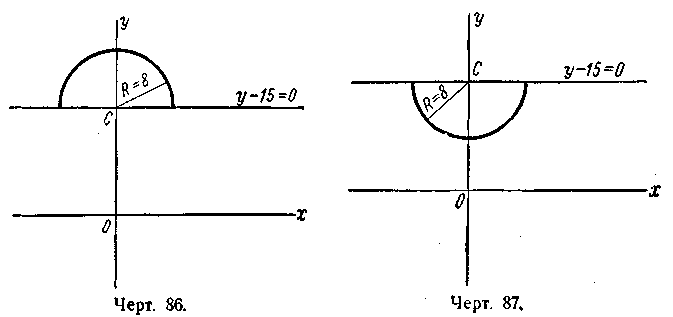
(черт. 86); 6) полуокружность радиуса R = 8 с центром С(0; 15), расположенная под прямой у— 15 = 0 (черт. 87); 7) полуокружность радиуса R = 3 с центром С (—2; 0), расположенная влево от прямой x + 2;=0 (черт. 88); 8) полуокружность радиуса R = 3 с центром С (—2; 0), расположенная вправо от прямой x +2 = 0 (черт. 89); 9) полуокружность радиуса R = 5 с центром С (—2; —3), расположенная под прямой у + 3 = 0 (черт. 90); 10) полуокружность радиуса R = 7 с центром С (— 5; — 3), расположенная вправо от прямой x + 5 = 0 (черт. 91). 399. 1) Вне окружности; 2) на окружности; 3) внутри окружности; 4) на окружности; 5) внутри окружности. 400. 1) х + 5у — 3 = 0; 2) х + 2 = 0; 3) 3х — у — 9 = 0; 4) у + 1 = 0. 401. 2x — 5у +19 = 0. 402. а) 7; б) 17; в) 2. 403. M1(—1; 5) и М2(—2; —2).

404. 1)
Пересекает окружность; 2) касается
окружности; 3) проходит вне окружности.
405.
1) | k
| <
![]() ;
2) k
= ±
;
2) k
= ±
![]() ;
3) | k|
>
;
3) | k|
>
![]() .
406.
.
406.
![]() .
407. 2x
+ у
— 3
= 0. 408.
11x
— 7y
— 69
= 0. 409.
2
.
407. 2x
+ у
— 3
= 0. 408.
11x
— 7y
— 69
= 0. 409.
2![]() .
410.
2x
— 3y
+ 8 = 0, 3x
+ 2y
—14
= 0. 412.
x2
+ y2
+ 6x
— 9y
— 17 =
0.
.
410.
2x
— 3y
+ 8 = 0, 3x
+ 2y
—14
= 0. 412.
x2
+ y2
+ 6x
— 9y
— 17 =
0.

413. 13x2
+ 13у
+ 3x
+ 71у
= 0. 414.
7x
—4у
= 0. 415.
2. 416.
10. 417.
(х +
3)' + (у
– 3)2
=10. 418.
х —
2у
+ 5 = 0. 419.
3x
— 4у
+ 43 = 0. 420.
M1(—![]() ;
;
![]() );
d
= 2
);
d
= 2![]() .
421.
x1x
+ y1y
= R2.
422.
(x1
— α)(x
—
α)
+ (y1
— β)(у
— β)
= R2.
423.
45°.
424.
90°. 425.
(α
— α)2
+ (β
— β)
=
.
421.
x1x
+ y1y
= R2.
422.
(x1
— α)(x
—
α)
+ (y1
— β)(у
— β)
= R2.
423.
45°.
424.
90°. 425.
(α
— α)2
+ (β
— β)
=
![]() .
427.
x
— 2y
— 5 = 0 и
2x
— y
— 5 = 0.
.
427.
x
— 2y
— 5 = 0 и
2x
— y
— 5 = 0.
4 28.
2x
+y
— 8 = 0 и x
— 2y
+ 11 = 0. 429.
2x
+ y
— 5 = 0, x
— 2y
= 0. 430.
90°. 431.
x
+ 2y
+ 5 = 0. 432.
d
= 7,5. 433. d
= 6. 434.
d
=
28.
2x
+y
— 8 = 0 и x
— 2y
+ 11 = 0. 429.
2x
+ y
— 5 = 0, x
— 2y
= 0. 430.
90°. 431.
x
+ 2y
+ 5 = 0. 432.
d
= 7,5. 433. d
= 6. 434.
d
=
![]() .
435.
3. 436.
2x
+ 4y
— 1 = 0 и 2x
+ y
+ 19 = 0. 437.
2x +
у — 5
= 0 и 2х
+ y
+ 5 = 0. 438.
= 2R cos (
— 0)
(черт.
92). 439.
1)
= 2R cos
(черт.
93); 2)
= —2 cos
(черт.
94); 3)
= 2R sin
(черт.
95); 4)
= — 2R sin
(черт.
96). 440.
1) (2; 0) и R
= 2; 2) (
.
435.
3. 436.
2x
+ 4y
— 1 = 0 и 2x
+ y
+ 19 = 0. 437.
2x +
у — 5
= 0 и 2х
+ y
+ 5 = 0. 438.
= 2R cos (
— 0)
(черт.
92). 439.
1)
= 2R cos
(черт.
93); 2)
= —2 cos
(черт.
94); 3)
= 2R sin
(черт.
95); 4)
= — 2R sin
(черт.
96). 440.
1) (2; 0) и R
= 2; 2) (![]() ;
;
![]() )
и R
=
)
и R
=
![]() ;
3) (1; ).
R
= 1; 4) (
;
3) (1; ).
R
= 1; 4) (![]() —
—![]() ;)
и R
=
;)
и R
=
![]() ;
5) (3; 4) и R
= 3; 6 (4;
;
5) (3; 4) и R
= 3; 6 (4;
![]() )
и R=
4; 7) (4; —
)
и R=
4; 7) (4; —![]() )
и R
= 4. 441.
1) x2
+ y2
— 3x
= 0; 2) x2
+ y2
+ 4 = 0; 3) х2
+ y2
— х + у = 0.
442. 1)
= cos ;
2)
= —3 cos ;
3)
= 5 sin ;
4)
= — sin ;
)
и R
= 4. 441.
1) x2
+ y2
— 3x
= 0; 2) x2
+ y2
+ 4 = 0; 3) х2
+ y2
— х + у = 0.
442. 1)
= cos ;
2)
= —3 cos ;
3)
= 5 sin ;
4)
= — sin ;

5)
= cos
+ sin .
443.
= R cos (
— 0).
444.
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() 4)
4)
![]() 5)
5)
![]() 6)
6)
![]() 7)
7)
![]() 8)
8)
![]() 9)
9)
![]() или
или
 10)
10)
![]() 447.
1)
447.
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]() 6)
6)
![]() 446.
1) 4 и 3; 2) 2 и
1; 3) 5 и
1; 4)
446.
1) 4 и 3; 2) 2 и
1; 3) 5 и
1; 4)
![]() и
и
![]() ;
5)
;
5)
![]() и
и
![]() 6)
6)
![]() и
и
![]() 7) 1 и
7) 1 и
![]() 8) 1 и 4
9)
8) 1 и 4
9)
![]() и
и
![]() 10)
10)
![]() и 1 447.
1) 5 и 3 ; 2)
F1(—4;
0), F2(4;
0), 3)
=
и 1 447.
1) 5 и 3 ; 2)
F1(—4;
0), F2(4;
0), 3)
=
![]() ;
4) x
=
;
4) x
= ![]() 448.
16 кв. ед. 449.
1)
448.
16 кв. ед. 449.
1)
![]() и 3; 2) F1(0;
—2), F2(0;
2); 3)
=
и 3; 2) F1(0;
—2), F2(0;
2); 3)
=
![]() ;
4) y
= ±
;
4) y
= ±
![]() .
450.
.
450.
![]() кв. ед. 451.
кв. ед. 451.
![]() .
452.
См. черт. 97. 453. (—3;
—
.
452.
См. черт. 97. 453. (—3;
—![]() ),
(—3;
),
(—3;
![]() ).
454.
Точки A1
и A6
лежат на эллипсе; A2,
A4
и A
8 — внутри эллипса;
).
454.
Точки A1
и A6
лежат на эллипсе; A2,
A4
и A
8 — внутри эллипса;

A3,
A
5, A7,
A9
и
A10
— вне
эллипса.
455.
1) Половина эллипса
![]() расположенная в верхней полуплоскости
(черт. 98); 2) половина эллипса
расположенная в верхней полуплоскости
(черт. 98); 2) половина эллипса
![]() ,
расположенная в нижней полуплоскости
(черт. 99,); 3) половина эллипса
,
расположенная в нижней полуплоскости
(черт. 99,); 3) половина эллипса
![]() расположенная
в левой полуплоскости (черт.
100); 4) половина эллипса
расположенная
в левой полуплоскости (черт.
100); 4) половина эллипса
![]() расположенная
в правой полуплоскости
(черт. 101). 456.
15. 457.
8. 458.
5x +
12у
+ 10 = 0, х
— 2
= 0. 459. r1
= 2,6, r2
= 7,4. 460.
20. 461.
10.
расположенная
в правой полуплоскости
(черт. 101). 456.
15. 457.
8. 458.
5x +
12у
+ 10 = 0, х
— 2
= 0. 459. r1
= 2,6, r2
= 7,4. 460.
20. 461.
10.  462.
(—5; 3
462.
(—5; 3![]() и
(—5; — 3
и
(—5; — 3![]() ).
463.
(— 2;
).
463.
(— 2;
![]() )
и
(— 2; —
)
и
(— 2; —![]() ).
464.
3 и 7. 465.
1)
).
464.
3 и 7. 465.
1)
![]() 2)
2)
![]() 3)
3)
![]() 3)
3)
![]() 5)
5)
![]() 6)
6)
![]() 6)
6)
![]() 466. 1)
466. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
467.
.
467.
![]() .
468. 471.
1) С (3; —1), полуоси 3 и
.
468. 471.
1) С (3; —1), полуоси 3 и
![]() ,
,
![]() .
уравнения
директрис: 2x
— 15 =
0, 2y
+ 3 = 0; 2) С(—
1; 2), полуоси 5 и 4,
.
уравнения
директрис: 2x
— 15 =
0, 2y
+ 3 = 0; 2) С(—
1; 2), полуоси 5 и 4,
![]() .
уравнения директрис:
3x
— 22 = 0; 3x
+ 28 = 0; 3) С(1;
— 2), полуоси 2
.
уравнения директрис:
3x
— 22 = 0; 3x
+ 28 = 0; 3) С(1;
— 2), полуоси 2![]() и 4,
и 4,
![]() .
уравнения директрис:
у — 6 = 0, у + 10 = 0. 472.
1) Половина эллипса
.
уравнения директрис:
у — 6 = 0, у + 10 = 0. 472.
1) Половина эллипса
![]() =
1 расположенная
над прямой у
+ 7 = 0 (черт. 102); 2) половина
эллипса
=
1 расположенная
над прямой у
+ 7 = 0 (черт. 102); 2) половина
эллипса
![]() =
1 расположенная
под прямой
у — 1 = 0 (черт. 103); 3)
половина эллипса
=
1 расположенная
под прямой
у — 1 = 0 (черт. 103); 3)
половина эллипса
![]() =
1 , расположенная в
левой полуплоскости (черт. 104); 4) половина
эллипса
=
1 , расположенная в
левой полуплоскости (черт. 104); 4) половина
эллипса
![]() =
1 расположенная
вправо от прямой x
+ 5 = 0. (черт. 105). 473.
1)
=
1 расположенная
вправо от прямой x
+ 5 = 0. (черт. 105). 473.
1)
![]() =
1 2) 2x2
— 2xy
+ 2у2
- 3 = 0; 3) 68x2
+ + 48xy
+ 82у2
— 625 = 0; 4) 11х2
+ 2ху + 11ys
— 48x
— 48y
— 24 = 0. 474.
5x2
+ 9y2
+ 4x
— 18y
— 55 = 0. 475.
4x2
+ 3y
+ 32x
— 14у
+ 59 = 0. 476.
4x2
+ 5y2
+ 14x
+ 40y
+ 81 =0. 477.
7x2
— 2xy
+ 7у2
— 46x
+ 2y
+ 71 = 0. 478. 17x2
+ 8xу
+ 23у2
+ 30x
— 40y
— 175 = 0. 479.
x2
+ 2y2
— 6x
+ 24y
+ 31 = 0. 480. (4;
=
1 2) 2x2
— 2xy
+ 2у2
- 3 = 0; 3) 68x2
+ + 48xy
+ 82у2
— 625 = 0; 4) 11х2
+ 2ху + 11ys
— 48x
— 48y
— 24 = 0. 474.
5x2
+ 9y2
+ 4x
— 18y
— 55 = 0. 475.
4x2
+ 3y
+ 32x
— 14у
+ 59 = 0. 476.
4x2
+ 5y2
+ 14x
+ 40y
+ 81 =0. 477.
7x2
— 2xy
+ 7у2
— 46x
+ 2y
+ 71 = 0. 478. 17x2
+ 8xу
+ 23у2
+ 30x
— 40y
— 175 = 0. 479.
x2
+ 2y2
— 6x
+ 24y
+ 31 = 0. 480. (4;
![]() ),
(3;
),
(3;
![]() ) — прямая
касается эллипса. 482.
Прямая проходит вне эллипса. 483.
1) Прямая пересекает эллипс; 2) проходит
вне эллипса; 3) касается эллипса. 484.
1) При |m|<5
— пересекает эллипс; 2) при т
= ± 5 — касается эллипса;
3) при ) |т |
> 5 — проходит вне эллипса. 485.
k2a2
+b2
=m2.
486.
) — прямая
касается эллипса. 482.
Прямая проходит вне эллипса. 483.
1) Прямая пересекает эллипс; 2) проходит
вне эллипса; 3) касается эллипса. 484.
1) При |m|<5
— пересекает эллипс; 2) при т
= ± 5 — касается эллипса;
3) при ) |т |
> 5 — проходит вне эллипса. 485.
k2a2
+b2
=m2.
486.
![]() ;
488.
3x
+ 2у
— 10
= 0
и 3x
+ 2y
+ 10
= 0.
489.
х +
y
— 5
= 0
и x
+ y
+ 5 = 0,
490.
2x
— у —12
= 0,
2х
— 2y
+ 12 = 0; d
=
;
488.
3x
+ 2у
— 10
= 0
и 3x
+ 2y
+ 10
= 0.
489.
х +
y
— 5
= 0
и x
+ y
+ 5 = 0,
490.
2x
— у —12
= 0,
2х
— 2y
+ 12 = 0; d
=
![]() .
491.
M1(—
3; 2);
d
=
.
491.
M1(—
3; 2);
d
=
![]() .
492.
x
+ y
— 5 = 0 и x+
4y
— 10 = 0. 493.
4x —
5у
— 10 = 0. 494.
d
= 18. 495.
.
492.
x
+ y
— 5 = 0 и x+
4y
— 10 = 0. 493.
4x —
5у
— 10 = 0. 494.
d
= 18. 495.
![]() ,
ли
,
ли
![]() .
496.
.
496.
![]() .
499.
.
499.
![]()

Указание.
Воспользоваться
свойством эллипса, сформулированным в
задаче 498.
500.
![]() .
Указание. Воспользоваться свойством
эллипса, сформулированным в задаче 498.
502.
2x +
11у
— 10
= 0. Указание. Восполь
зоваться свойством эллипса,
.
Указание. Воспользоваться свойством
эллипса, сформулированным в задаче 498.
502.
2x +
11у
— 10
= 0. Указание. Восполь
зоваться свойством эллипса,

сформулированным в задаче
501. 503.
(3; 2) и (3;
— 2). 504.
![]() .
505.
10,5
.
505.
10,5![]() .
506.
= 60°. 507.
16,8. 508.
60°. 509.
В эллипс, уравнение которого
.
506.
= 60°. 507.
16,8. 508.
60°. 509.
В эллипс, уравнение которого
![]() .
510.
x2
+ y2
– 0, 511.
.
510.
x2
+ y2
– 0, 511.
![]() .
512. q
=
.
512. q
=
![]() 513. q
=
513. q
=
![]() 514.
q1
=
514.
q1
=
![]() q2
=
q2
=
![]() 515. 1)
515. 1)
![]() .
2)
.
2)
![]() 3)
3)
![]() .
4)
.
4)
![]() 5)
5)
![]() .
6)
.
6)
![]() 7)
7)
![]() .
8)
.
8)
![]() 9)
9)
![]() 516.
1)
516.
1)
![]() 2)
2)
![]() .
3)
.
3)
![]() .
4)
.
4)
![]() .
5)
.
5)
![]() .
517.
1)
a
= 1,
b
= 2; 2) a
= 4,
b
= 1; 3) a
= 4,
b
= 2; 4) a
= 1,
b
= 1; 5) a
=
.
517.
1)
a
= 1,
b
= 2; 2) a
= 4,
b
= 1; 3) a
= 4,
b
= 2; 4) a
= 1,
b
= 1; 5) a
=
![]() ,
b
=
,
b
=
![]() ;
6) a
=
;
6) a
=
![]() ,
b
=
,
b
=
![]() ;
7) a
=
;
7) a
=
![]() ,
b
=
,
b
=
![]() ;
518.
1) a
= 3, b
= 4; 2)
F2(—5;
0), F2(5;
0); 3)
=
;
518.
1) a
= 3, b
= 4; 2)
F2(—5;
0), F2(5;
0); 3)
=
![]() ;
4)
y
=
±
;
4)
y
=
±
![]() 5) x
=
±
5) x
=
±
![]() 519.
1) a
= 3, b
= 4; 2) F1(0;
-5), F2(0;
5); 3)
=
519.
1) a
= 3, b
= 4; 2) F1(0;
-5), F2(0;
5); 3)
=
![]() ;
4)
y
=
±
;
4)
y
=
±
![]() 5) y
=
±
5) y
=
±
![]() 520.
12 кв. ед. 521.
1) Часть гиперболы
520.
12 кв. ед. 521.
1) Часть гиперболы
![]() ,
расположенная в
верхней полуплоскости (черт. 106); 2) ветвь
гипер-
,
расположенная в
верхней полуплоскости (черт. 106); 2) ветвь
гипер-

болы
![]() ,
расположенная в нижней полуплоскости
(черт. 107); 3) ветвь гиперболы
,
расположенная в нижней полуплоскости
(черт. 107); 3) ветвь гиперболы
![]() ,
расположенная в
левой полуплоскости
,
расположенная в
левой полуплоскости

(черт. 108); 4) ветвь гиперболы
![]() расположенная в верхней полуплоскости
(черт. 109). 522. x
+ 4
расположенная в верхней полуплоскости
(черт. 109). 522. x
+ 4![]() + 10 = 0 и x
— 10 = 0. 523.
r1
= 2
+ 10 = 0 и x
— 10 = 0. 523.
r1
= 2![]() ,
r2
= 10
,
r2
= 10![]() .
524. 8.
525. 12.
526. 10.
527. 27.528.
(10;
.
524. 8.
525. 12.
526. 10.
527. 27.528.
(10;
![]() )
и (10; —
)
и (10; —
![]() )
529.
(—6; 4
)
529.
(—6; 4![]() )
и (—6; — 4
)
и (—6; — 4![]() ).
530.
2
).
530.
2![]() и 26
и 26![]() .
531.
См. черт. 110. 532.
1)
.
531.
См. черт. 110. 532.
1)
![]() ;
2) x2
— y2
= 16; 3)
;
2) x2
— y2
= 16; 3)
![]() .
или
.
или
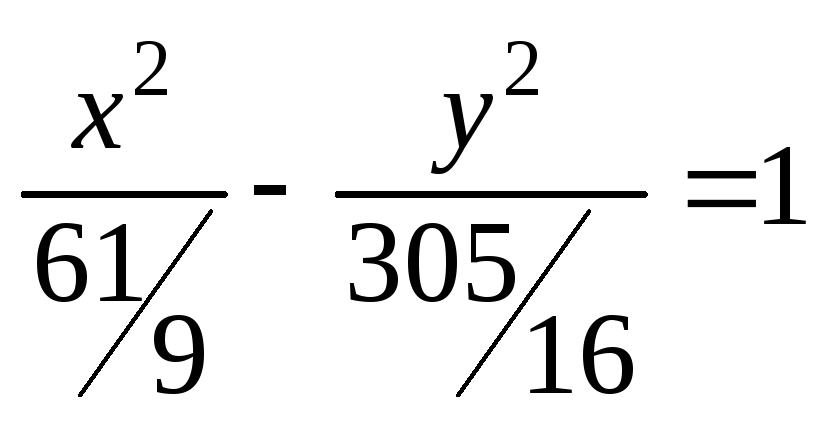 4)
4)
![]() ;
5)
;
5)
![]() ;
534.
=
;
534.
=
![]() .
535.
1)
.
535.
1)
![]() ;
536.
;
536.
![]() .
540.
1)
.
540.
1)
![]() 2)
2)![]()
5 41.
1)
С (2;
—3), а
= 3, b
= 4,
= 5/3, уравнения директрис:
5x —
1 = 0, 5x
— 19 = 0, уравнения асимптот: 4x
— 3y
— 17= 0, 4х
+ 3у
+ 1 = 0; 2) С(—5;
1), a
= 8, b
= 6,
= 1,25; уравнения директрис: х=—11,4
и x=
1,4, уравнения асимптот:
3x +
4y
+ 11 = 0 и 3x
— 4y
+ 19 = 0; 3) C(2;
—1), a
= 3, b
= 4,
= 1,25, уравнения директрис:
y
= — 4,2, y
= 2,2, уравнения асимптот: 4x
+ 3y
— 5 = 0, 4х
— 3у
— 11 = 0. 542. 1) Часть
гиперболы
41.
1)
С (2;
—3), а
= 3, b
= 4,
= 5/3, уравнения директрис:
5x —
1 = 0, 5x
— 19 = 0, уравнения асимптот: 4x
— 3y
— 17= 0, 4х
+ 3у
+ 1 = 0; 2) С(—5;
1), a
= 8, b
= 6,
= 1,25; уравнения директрис: х=—11,4
и x=
1,4, уравнения асимптот:
3x +
4y
+ 11 = 0 и 3x
— 4y
+ 19 = 0; 3) C(2;
—1), a
= 3, b
= 4,
= 1,25, уравнения директрис:
y
= — 4,2, y
= 2,2, уравнения асимптот: 4x
+ 3y
— 5 = 0, 4х
— 3у
— 11 = 0. 542. 1) Часть
гиперболы
![]() , расположенная над
прямой у + 1 = 0 (черт. 111); 2) ветвь гиперболы
, расположенная над
прямой у + 1 = 0 (черт. 111); 2) ветвь гиперболы
![]() расположенная
под прямой y
—7 = 0 (черт. 112); 3) ветвь гиперболы
расположенная
под прямой y
—7 = 0 (черт. 112); 3) ветвь гиперболы
![]() расположенная
влево от прямой x
— 9 = 0 (черт. 113); 4) часть гиперболы
расположенная
влево от прямой x
— 9 = 0 (черт. 113); 4) часть гиперболы
![]() расположенная влево от
расположенная влево от
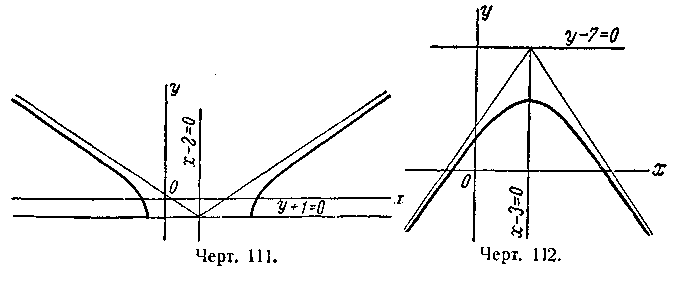

 прямой
х —
5 = 0 (черт. 114), 543.
1)
прямой
х —
5 = 0 (черт. 114), 543.
1)
![]() 2) 24xy
+ 7y2
— 144 = 0; 3) 2xy
+ 2x
— 2у
+ 7 = 0. 544.
2) 24xy
+ 7y2
— 144 = 0; 3) 2xy
+ 2x
— 2у
+ 7 = 0. 544.
![]() 545.
545.
![]() 546.
x2
— 4у2
— 6x
— 24y
— 47 = 0. 547.
7x2
— 6xy
— y2
+ 26x
— 18y
— 17 = 0. 548.
91x2
— 100xу
+ 16у2
— 136x + 84y
— 47 = 0. 549.
xу
=
546.
x2
— 4у2
— 6x
— 24y
— 47 = 0. 547.
7x2
— 6xy
— y2
+ 26x
— 18y
— 17 = 0. 548.
91x2
— 100xу
+ 16у2
— 136x + 84y
— 47 = 0. 549.
xу
=
![]() при повороте старых осей на угол — 45°;
ху = —
при повороте старых осей на угол — 45°;
ху = —
![]() при
повороте на угол +
45°.
при
повороте на угол +
45°.
550. 1)
С(0;
0), а = b
= 6,
уравнения асимптот:
x
= 0 и у = 0;
2) С(0;
0), a
= b
= 3, уравнения асимптот: x
= 0 и y
= 0; 3) С(0;
0), а =
b
= 5, уравнения асимптот: x
= 0 и у
= 0. 551.
(6; 2) и (![]() .
552. (
.
552. (![]() )
- прямая
касается гиперболы. 553.
Прямая проходит вне гиперболы. 554.
1) Касается гиперболы;
2) пересекает гиперболу в двух точках;
3) проходит вне гиперболы. 555.
1) При |m|
>
4,5 — пересекает
гиперболу; 2) при т
= ± 4,5 -
касается гиперболы; 3) при |т|
< 4,5 –
про-ходит вне гиперболы. 556.
k2а2
— b2
= т2.
557.
)
- прямая
касается гиперболы. 553.
Прямая проходит вне гиперболы. 554.
1) Касается гиперболы;
2) пересекает гиперболу в двух точках;
3) проходит вне гиперболы. 555.
1) При |m|
>
4,5 — пересекает
гиперболу; 2) при т
= ± 4,5 -
касается гиперболы; 3) при |т|
< 4,5 –
про-ходит вне гиперболы. 556.
k2а2
— b2
= т2.
557.
![]() 559.
3х — 4у — 10
= 0, 3х — 4у
+ 10 = 0. 560.
10x
— 3у
—32 = 0, 10x
—3y
+ 32 = 0. 561.
x
+ 2y
— 4 = 0, x
+ 2y
+ 4 = 0; d
=
559.
3х — 4у — 10
= 0, 3х — 4у
+ 10 = 0. 560.
10x
— 3у
—32 = 0, 10x
—3y
+ 32 = 0. 561.
x
+ 2y
— 4 = 0, x
+ 2y
+ 4 = 0; d
=
![]() 562.
M1(—6;
3); d
=. 563.
5х —
3у
— 16 = 0, 13x
+ 5y
+ 48 = 0. 564.
2x
+ 5y
— 16
= 0. 565.
d
=
562.
M1(—6;
3); d
=. 563.
5х —
3у
— 16 = 0, 13x
+ 5y
+ 48 = 0. 564.
2x
+ 5y
— 16
= 0. 565.
d
=
![]() .
566.
.
566.
![]() ,
,
![]() .
567.
.
567.
![]() .
568. х
= — 4,
х = 4,
у = — 1,
у = 1.
572.
.
568. х
= — 4,
х = 4,
у = — 1,
у = 1.
572.
![]() .
573.
.
573.
![]() .
575.
2x
+ y
+ 6 = 0. Указание. Воспользоваться
свойством гиперболы, сформулированным
в задаче 574.
577. x2
— у2
= 16. 578.
.
575.
2x
+ y
+ 6 = 0. Указание. Воспользоваться
свойством гиперболы, сформулированным
в задаче 574.
577. x2
— у2
= 16. 578.
![]() .
579.
.
579.
![]() .
580.
q
=
.
580.
q
=
![]() .
581. q
= 2. 582.
q1
= 2, q2
= у.
583.
1) y2
= 6x;
2) у2
= —x.
3) x2
=
.
581. q
= 2. 582.
q1
= 2, q2
= у.
583.
1) y2
= 6x;
2) у2
= —x.
3) x2
=
![]() ;
4) x2
= — 6y.
584.
1) p
= 3; в правой полуплоскости сниметрично
оси Ох; 2)
р =
2,5; в верхней полуплоскости симметрично
оси Оу; 3)
р =
2; в левой полуплоскости симметрично
оси Ох; 4)
р =
;
4) x2
= — 6y.
584.
1) p
= 3; в правой полуплоскости сниметрично
оси Ох; 2)
р =
2,5; в верхней полуплоскости симметрично
оси Оу; 3)
р =
2; в левой полуплоскости симметрично
оси Ох; 4)
р =
![]() ;
в нижней полуплоскости
симметрично оси Оу.
585.
1) у2
= 4х; 2) у2
= — 9x;
3) x2
= у;
;
в нижней полуплоскости
симметрично оси Оу.
585.
1) у2
= 4х; 2) у2
= — 9x;
3) x2
= у;

4) x2 = — 2у. 586. 40 см. 587. x2 = — 12у. 588. 1) Часть параболы у2 = 4x; расположенная в первом координатном углу (черт. 115); 2) часть параболы

у2 = — х, расположенная во втором координатном углу (черт. 116); 3) часть параболы у2 = — 18x, расположенная в третьем координатном углу (черт. 117);

4) часть параболы у2 — 4х, расположенная в четвёртом координатном углу (черт. 118); 5) часть параболы x2 = 5у, расположенная в первом координатном углу (черт. 119); 6) часть параболы x2 == — 25у, расположенная в третьем координатном углу (черт. 120); 7) часть параболы x2 = 3y, расположенная во втором координатном углу (черт. 121); 8) часть параболы x2 = — 16у, расположенная в четвёртом координатном углу (черт. 122).

589. F(6;
0), х
+ 6 = 0. 590.
12. 591.
6. 592.
(9; 12), (9; — 12). 593.
y2
= — 28x.
594.
1) (у —
β)
= 2р(х
— α); 2) (у
—β)2
= — 2р(х
— α).
595.
1) (x
— α )2
= 2р(у
— β);
2) (x
—α)2
= — 2р(у
— β).
596.
1) А(2;
0), p
= 2, x
— 1 = 0; 2) А(![]() 0),
р =
3, 6x
—13 = 0; 3) А(0;
—
0),
р =
3, 6x
—13 = 0; 3) А(0;
—![]() ).
р
= 3, 6y
— 13 = 0; 4) А(0;
2), p
=
).
р
= 3, 6y
— 13 = 0; 4) А(0;
2), p
=
![]() ;
4y
— 9 = 0. 597.
1) А(—2;
1), р
= 2; 2) А(1;
3),
;
4y
— 9 = 0. 597.
1) А(—2;
1), р
= 2; 2) А(1;
3),
