
книги из ГПНТБ / Шумоподобные сигналы в системах передачи информации
..pdf
частотные рассогласования не превышают величины |
m (| щ |) = |
||||||||
= 0,6V"^3 . |
|
|
|
|
|
|
|
|
|
Среднеквадратичное |
отклонение |
выбросов на всей |
плоскости |
т, |
|||||
Q в пределах + Ts ; |
+ |
2 я / Г э |
равно |
"jAO («б ) = 0,5іАѴэ , |
] / D ( | u 6 | ) |
= |
|||
= 0,35 У Ng. При исключении |
области больших частотных |
расстроек |
|||||||
, Щ ^ ) = о , б ] / л г , |
ѴЩЫ) |
= олѴЩ. |
|
|
|
|
|||
|
3.2.4. Двумерные и одномерные функции |
|
|
|
|
||||
|
взаимной корреляции сигналов Хаффмена |
|
|
|
|
||||
Если на вход фильтра, согласованного с сигналом |
Sh |
(t), |
посту |
||||||
пает сигнал St (t), имеющий некоторое временное и частотное |
смеще |
||||||||
ние т, |
то в зависимости от режима работы может появляться либо |
||||||||
ДАФВК, либо ДПФВК. Расчет ДАФВК и ДПФВК может быть про изведен в соответствии с выражением (3.2.7), если под х понимать Sh (t),
а под у — St (t).
Поскольку в ряде систем передачи информации с кодовым разде лением адресов частотный сдвиг между сигналами может отсутствовать, то ДФВК вырождаются в ФЗ К при Q = 0.
Одномерные функции взаимной корреляции M-последовательностей.
По виду ФВК можно судить о степени ортогональности сигналов, от носящихся к ансамблю рассматриваемого типа. /И-последовательности не являются ортогональными сигналами, поэтому можно говорить лишь об их квазиортогональности при необходимых длительностях ІѴэ, при которых уже обеспечивается необходимое отношение боковых выбросов ФВК к основному выбросу ФАК. Именно этим отношением характеризуется степень ортогональности анализируемых сигналов.
Разработчиков радиосистем интересуют различные ФВК. Могут представлять интерес апериодические (АФВК), периодические (ПФВК), смешанно-периодические или стыковые функции взаимной корреляции (СФВК), а также мендро-инвертированные авто- и взаимокорреля ционные функции (МИФАК и МИФВК).
Взаимное положение сигналов во времени для этих случаев дано на рис. 3.2.7.
Образование АФВК и ПФВК пояснено в гл. 2. СФВК появляются в том случае, когда на вход фильтра, согласованного с последователь ностью S h, поступают поочередно без интервалов две другие последо вательности 5; и Sr. Подобный случай может иметь место в многоад ресной асинхронной системе связи с кодовым разделением адресов [3.15]. Если же в радиосистеме осуществляется слежение за принимае
мым сигналом с точностью до фазы, то можно для передачи |
двоичной |
||||
информации |
использовать основную Sh и |
негативную 5 Г Г |
(противо |
||
положную) |
M-последовательности |
[3.17]. |
В этом случае, |
если на |
|
фильтр, |
согласованный с последовательностью Sk, вслед за Sh посту |
||||
пает STr, |
то на его выходе мы получаем МИФАК. Если же приемник |
||||
согласован с Sh то образуется МИФВК.
121
При анализе ФВК представляют интерес их различные характе
ристики: |
|
|
выбросов иб |
|
|
|
1. |
Значения |
наибольших боковых |
м а к с и |
их коли |
||
чество. |
|
|
|
|
|
|
2. |
Величина |
математического ожидания модуля |
выбросов т ( | ы б | ) |
|||
и значения выбросов m |
(и5). |
|
|
|
||
3. |
Процент |
выбросов, превышающих некоторый порог |
« п о р . |
|||
4. |
Значение |
среднеквадратичного |
отклонения |
модуля |
выбросов |
|
^ 1 / 2 (I "б I) и значения |
выбросов D ' / 2 |
(и о)- |
|
|
||
5- ^ м а и с = " - ^ ^ - 1 0 0 % .
иО С Н
6.Y c p = = ^ i l i f 6 J L . i o o % .
мО С П
7.Плотность распределения выбросов и модуля выбросов.
АФВКI |
st |
"J—»- |
I |
st |
I |
"|—*> |
I S k |
I |
|
/70ДЛІ |
Sft |
I |
|
f0j?A4 |
5* |
I |
ШФАК\ sk или sL |
I |
МИФВК |
|
||
|
|
|
Рис. 3.2.7. |
|
|
|
|
|
Рассмотрим различные ФВК и их характеристики. |
|
|||||||
Апериодические |
|
ФВК. На |
рис. 3.2.8 |
в качестве примера |
приведен |
|||
вид АФВК для последовательностей |
1 * и 3* в соответствии с табл. 3.2.1, |
|||||||
который является типичным для Nэ |
= |
127. Расчеты |
АФВК с исполь |
|||||
зованием ЭВМ производились |
для |
N 9 |
— \Ъ, 31, |
63, |
127, |
255, 511, |
||
1023 и 2047. Статистическая обработка результатов расчета позволила
установить их стабильную зависимость от длительности |
последователь |
|||||||||||||
ностей Na. |
Значения наибольших |
боковых выбросов иб |
м а к с |
находятся |
||||||||||
в пределах |
(1,4 -ь 5,l)l/Afa . Количество наибольших выбросов |
N6 |
м а к 0 |
|||||||||||
редко бывает больше одного. Математическое ожидание модуля |
выбро |
|||||||||||||
са |
m (|u6 |) |
= 0,54y^iVg. Среднеквадратичное отклонение модуля вы |
||||||||||||
броса |
определяется выражением |
D 1 |
/ 2 |
(| иб |) = 0,5|/"Л/Э . Математичес |
||||||||||
кое |
ожидание |
выбросов |
m (и5) |
= |
0, |
среднеквадратичное |
значение |
|||||||
D ' / 2 |
(ив) - |
0,7бѴЩ. |
|
|
|
|
|
|
|
|
|
|||
|
Периодические |
ФВК- |
Аналогично |
были |
найдены |
статистические |
||||||||
характеристики |
и ПФВК |
[3.40]. На |
рис. 3.2.9 |
приведен типичный |
вид |
|||||||||
ПФВК M-последовательностей 1 и 3* в соответствии с табл. 3.2.1 |
при |
|||||||||||||
N9 |
= |
127. |
Обобщение результатов многочисленных расчетов показа |
|||||||||||
ло, что значения |
наибольших боковых выбросов находятся |
в пределах |
||||||||||||
" б м а к с = |
(1>5 -f- |
6)]/ЛѴ |
Количество |
наибольших выбросов |
ПФВК |
|||||||||
122 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xtt,Ö)N3
АФВК
ПФВК |
30 |
t*3* xfcW
N3--m
Рис. 3.2.10.
123
у некоторых сочетаний М-последователыюстей может быть большим, но при этом они не превышают уровня 1,5|'' /Ѵэ . В этом случае мы полу
чаем так называемые трехуровневые ПФВК |
(ПФВК'Г) [3.43J. В |
ка |
|||||||||||
честве примера |
на |
рис. 3.2.10 приводится |
ПФВКТ |
для |
ІѴэ = |
127. |
|||||||
Математическое |
ожидание |
модуля |
выброса |
оказывается |
равным |
||||||||
m (I и о J) = 0 , 8 ] / N э ; |
среднеквадратичное отклонение модуля |
выброса |
|||||||||||
D ' / 2 |
(|иб |
]) = |
0№УЖа. |
Значение выбросов |
|
у ПФВК |
т(и6) |
= 0, |
|||||
О 1 / 2 |
(ио) |
= |
YNa. |
|
для |
боковых |
|
выбросов |
рассмотрена |
||||
|
Функция |
распределения |
|
||||||||||
в гл. 2 (см. также [3.16]). При одновременном действии более чем |
4—5 |
||||||||||||
сигналов с большими базами происходит нормализация |
распределения |
||||||||||||
значения |
суммарных |
боковых выбросов. |
|
|
|
|
|
|
|||||
|
Смешанно-периодические |
ФВК. |
Анализ |
статистических |
характе |
||||||||
ристик смешанно-периодических ФВК позволил установить, что вели
чина максимальных боковых выбросов находится в пределах иб |
м а к с |
= |
||||||
=--•= (2 ~ 5,\)YNъ . Математическое ожидание модуля выброса m (| uö |
|) = |
|||||||
— 0,80]/Л/э , |
а среднеквадратичное отклонение |
выброса |
D 1 / 2 |
(| и0\) |
-= |
|||
=0,60'|/"Л/ Э ; |
для значений |
выбросов |
m (и6) |
= |
0, Dl/2 |
(ыб) |
= ]Л/ѴЭ . |
|
Меандро-инвертированные |
ФА К- |
Обобщение |
результатов |
расчета |
||||
характеристик МИФАК /И-последовательностей показало, что макси
мальные боковые выбросы находятся |
в пределах |
«б м а к с = |
(1,3 |
н- |
|||||||
• f |
2,3)yr iVg. Математическое ожидание |
модуля |
выброса |
m (| и б |
|) |
= |
|||||
= |
0,66]//Ѵэ , |
для значения |
выбросов m (иб ) |
= 0, |
D 1 |
/ 2 (и б) |
= |
||||
= |
0,80]//Ѵэ ; |
среднеквадратичное |
отклонение |
модуля боковых |
вы |
||||||
бросов D 1 |
/ 2 |
(I и б I) = 0 50 )/./Ѵэ . |
Для значения |
выбросов |
m |
(и а) = |
0, |
||||
D ' / 2 (ыб) = |
0,80]//?;. |
|
|
|
|
|
|
ха |
|||
|
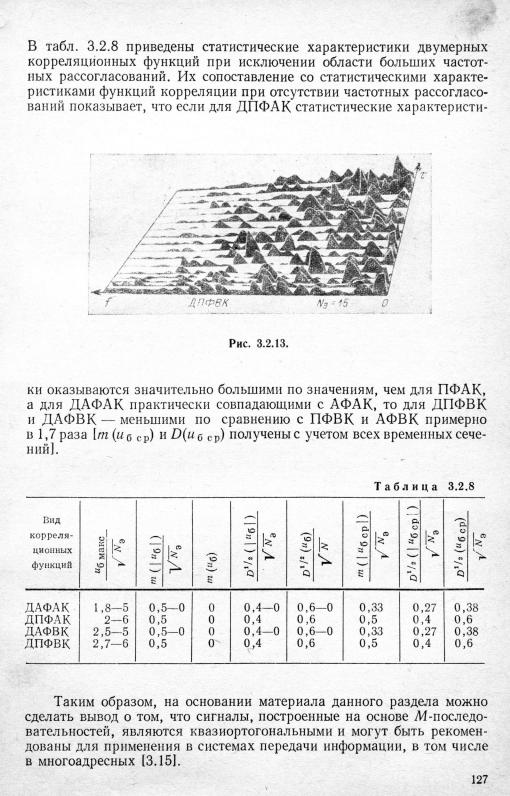
В табл. 3.2.7, являющейся сводной, приведены статистические |
||||||||||
рактеристики различных ФВК и статистические характеристики АФАК.
Двумерная функция взаимной корреляции. При наличии времен ного и частотного сдвига между опорным сигналом и воздействующим в зависимости от режима работы наблюдается либо ДАФВК. либо
ДПФВК, |
расчет которых может быть произведен в соответствии с вы |
||||||||||
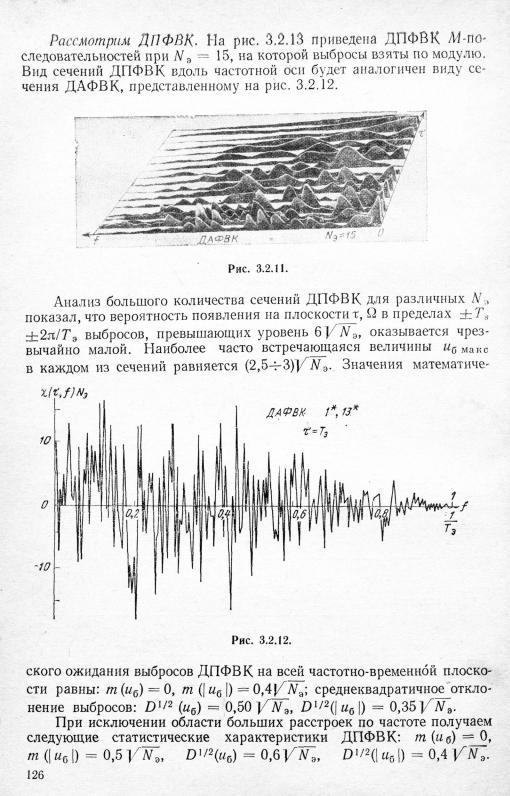
ражением (3.2.7). Парис. 3.2.11 изображены |
модули выбросов ДАФВК |
||||||||||
при УѴЭ = |
15. |
На |
рис. 3.2.12 показан |
вид |
сечения |
ДАФВК |
вдоль |
||||
частотной |
оси при |
N3 |
= |
127 для |
т = |
Тэ. |
Подобный |
вид является ти |
|||
пичным для различных |
сечений |
/И-последовательностей почти |
для |
||||||||
всей плоскости т, й в |
пределах ±Та; |
+ 2 я / 7 1 |
э . |
|
|
||||||
На основании |
расчетов сечений ДАФВК для различных N а |
с ис |
|||||||||
пользованием |
ЭВМ было установлено, что вероятность появления вы |
||||||||||
бросов tifj макс |
> |
6|/vVg |
оказывается |
ничтожно малой. Значения |
мате |
||||||
матического ожидания выбросов на всей частотно-временной |
плоскости |
||||||
при временных сдвигах сечений, кратных Т э |
, равны m |
{иб) |
= |
0, а для |
|||
модуля выбросов |
m (| и0 |
|) = 0,35|Л/ѴЭ -г- 0 (см. рис. 3.2.5), средне |
|||||
квадратичное отклонение |
выбросов 0 < Dl/2 |
(иб) ^ |
0,5]/'Nа , |
и |
для |
||
модуля выбросов |
0<_D{I2 |
(| иб |) <І 0,35]/ІѴэ . Меньшие значения |
ста- |
||||
124
Тип последователь |
Характе |
ности |
ристики |
|
|
|
|
АФАК |
|
|
|
|
|
ПФАК |
|
М-последователь- |
АФВК |
||||
|
ности |
|
ПФВКТ |
||
|
|
|
|
ПФВК |
|
|
|
|
|
СФВК |
|
|
|
|
|
МИФАК |
|
|
|
|
|
МИФВК |
|
образованВновь последованые тельности |
Одно |
исход |
АФАКТ |
||
ПФАКТ |
|||||
|
ное |
сочета |
|||
|
АФВК |
||||
|
|
ние |
|||
|
|
ПФВК |
|||
|
|
|
|
||
|
|
Разные |
АФВК |
||
|
исходные |
||||
|
ПФВК |
||||
|
сочетания |
||||
|
|
|
|
АФАК |
|
|
|
|
|
ПФАК |
|
Сегменты |
ЛІ-после- |
АФВК |
|||
дователыюстей |
|
ПФВК |
|||
|
|
||||
|
|
|
|
ФКСП и |
|
|
|
|
|
СФВК |
|
Случайные |
последо |
АФАК |
|||
ПФАК |
|||||
вательности |
|
|
АФВК |
||
|
|
|
|
ПФВК |
|
Случайные |
последо |
АФВК |
|||
вательности |
и М-по- |
||||
ПФВК * |
|||||
следовательности |
|||||
|
|||||
|
|
Т а б л и ц а |
3.2.7 |
"б маке |
т ( 1 % 1 ) |
оѴ. ( 1 и б I ) D'A ("б) |
|
|
У~"~в |
|
У Wo |
0,7—1,25 |
0,32 |
0,26 |
0,41 |
1/ уж3 |
|
0 |
0 |
1,4—5 |
0,54 |
0,48 |
0,73 |
1,5 |
0,76 |
0,67 |
1 |
1,9—6 |
0,80 |
0,62 |
1 |
2,0—5,1 |
0,83 |
0,62 |
1 |
1,3—2,3 |
0,66 |
0,49 |
0,82 |
. 2 - 3, 3 |
0,80 |
0,62 |
1 |
1,7—2,4 |
0,58 |
0,49 |
0,73 |
1,5 |
0,81 |
0,66 |
1 |
1 ,8—4 |
0,54 |
0,5 |
0,73 |
1 ,5—3,7 |
0,78 |
0,62 |
1 |
1,7—3 |
0,54 |
0,47 |
0,73 |
2,4—3,3 |
0,80 |
0,59 |
1 |
1,45—4,1 |
0,52 |
0,9 |
0,71 |
1,6—4,3 |
0,79 |
0,58 |
1 |
1,4—4,3 |
0,52 |
0,49 |
0,72 |
1,6—5,0 |
0,8 |
0,6 |
1 |
2—4 |
0,78 |
0,6 |
1 |
1,5—3,1 |
0,51 |
0,65 |
0,7 |
2—4 |
0,83 |
0,68 |
1 |
2,4—4,3 |
0,54 |
0,48 |
0,7 |
2,75—4,5 |
0,82 |
0,62 |
1 |
1,9—5,5 |
0,53 |
0,46 |
0,7 |
2,4—5 |
0,80 |
0,62 |
1 |
тистических характеристик соответствуют сечениям вдоль частотной оси при большем относительном временном сдвиге. Если же исключить
из |
рассмотрения область |
с большими частотными |
расстройками, то |
||||||
0 < |
m (|и_б I X 0,5УЖа; |
|
0 < |
D^2(u6) |
< |
0,6\/Жв; |
0 < D^2 |
(\иб\)^ |
|
^0,4УNа- |
В сечениях |
вдоль |
частотной |
оси с временными |
сдвигами, |
||||
кратными |
Т э /2, получаем |
следующие |
статистические характеристики: |
||||||
0 < т ( | м б |
| ) < 0 , 8 / л Г э ; |
|
0 < D > / 2 ( « б ) < 0,9]/лГэ ; |
0 < D 1 |
/ 2 ( | w G | ) < |
||||
< і / л г э .
125
3.2.5. Спектр сигналов Хаффмена
Спектр М-последовательностей может быть определен обычным образом:
|
6Г |
|
|
|
|
Если S3 |
[1 — (/ — l)T3] |
— элемент |
последовательности; |
d,- — симво |
|
лы, определяющие знак |
каждого из элементов, то |
|
|
||
|
|
|
2 — 1 |
|
|
|
fs (г'ш) f |
Sa(t)e-latdt |
S ^ е ,І( (/-1)0)7"> 4 |
(3.2.10) |
|
|
- о |
|
/=і |
|
|
Таким образом, спектр М-последовательности |
равен |
произведе |
|||
нию двух |
сомножителей |
|
|
|
|
f а(ів>) = , f 3 (/cû),fn o c (ico),
где fa (m) — спектр одиночного элемента, который зависит от формы его огибающей. Второй сомножитель . fп о с (г'со) определяется сложной структурой последовательности субимпульсов. Если последователь ность повторяющаяся, то
fs |
(/©) = fg |
(i(o) f n |
o c (t©) |
f |
„ о в |
(ко), |
|
( 3 . 2 . 1 1 ) |
где |
|
|
|
|
|
|
|
|
^ |
sin(A. |
cor/2) |
/ _ |
- ю |
Г |
A ^ o p L j . |
( 3 . 2 Л 2 ) |
|
|
sm(wr s /2) |
V |
|
|
2 |
/ |
|
|
Г 8 — период М-последовательности; |
І Ѵ П О В |
— |
число повторений [3 . 13] . |
|||||
Если функция |
автокорреляции |
шумоподобной |
последовательно |
|||||
сти известна,то нахождение ее амплитудного спектра проще осуществ лять пѵтем предварительного расчета ее энергетического спектра [3.24]
(см. гл". 2, § 2 . 7 ) .
Спектр периодической последовательности должен быть линей чатым (дискретным). Амплитуда 1-й гармоники ПФАК М-последова тельности будет
2 л 1 \ |
2 |
Г |
, . |
п , |
2лІ |
|
|
|
|
cos |
dt ----- |
|
|
о |
|
|
|
|
+ |
s |
i n 2 |
^ . |
. ( 3 _ 2 Л З ) |
|
я 2 /2 |
|
|
N.. |
|
постоянная составляющая равна
|
э |
з |
G e (0) = т т Ѵ |
[ |
0 ) Л = -^ |
^ |
J |
N: |
128
откуда следует, что постоянная составляющая амплитудного спектра M-последовательности
f.(0) = \Ga(0y>*\=a/No,
где а — амплитуда элементарного субимпульса (элемента). Амплитуда его 1-й гармоники соответственно равна
S { |
N3TE |
|2G[ |
2 n l )] |
1/2 |
2a |
( t f 8 + l ) l / 2 S i n |
. \ |
N3TJ |
|
ni |
|
||
Если |
сравнить |
полученный |
результат |
с амплитудным спектром |
||
периодической последовательности импульсов, период которой имеет ту же длительность, что ^-последовательность, а амплитуды равны, то окажется, что постоянные составляющие будут равны, а амплитуды
всех гармонических |
составляющих |
периодической |
M-последователь |
|
ности будут в I (A/g + |
I) 1 / 2 1 = |
2Ne/2 |
раз больше, чем у обычной перио |
|
дической последовательности |
импульсов. |
|
||
Спектр сигнала определяется огибающей последовательности без |
||||
учета множителя е'м ', т. е. не |
зависит от несущей, |
которая его лишь |
||
смещает на tos 0 - Поэтому вместо ФМн сигнала можно рассматривать его огибающую, т. е. видеопоследовательность. Ширина спектра /И-по-
следовательности A/s определяется частотой следования |
элементов / т , |
||||||||
которая равна величине обратной длительности элемента: / т |
= |
Afs = |
|||||||
= |
1/ГЭ . Расстояние между |
|
линиями |
в спектре |
равняется |
\ITS. |
|||
|
|
3.2.6. Сегменты ^-последовательностей |
|
|
|
||||
|
|
Разбивая Л+последовательность большой длительности N9 на |
|||||||
сегменты длительности Nc, |
можно получить большее число ШПС, рас |
||||||||
сматривая каждый из сегментов как самостоятельный |
сигнал |
[7.4]. |
|||||||
Если сегменты не перекрываются, то их число равно Nс н |
= N J (Nс —• |
||||||||
— |
1). Таким образом, при |
выборе необходимой длительности ІѴЭ мож |
|||||||
но обеспечить требуемое число псевдослучайных |
последовательностей. |
||||||||
Так, |
например, для М-последовательности Nэ |
= 21 9 — 1 = 524 287 |
|||||||
при |
длительности Nc = 127 |
NCH = |
524 287 : 127 = 4100. |
|
|
||||
|
|
Анализ корреляционных |
свойств |
сегментов |
М-последовательнос- |
||||
тей численными методами показал, что статистические характеристики их ФВК совпадают с соответствующими характеристиками М-последо-
вательностей |
той же длительности. Автокорреляционные |
свойства |
|||
сегментов М-последовательностей оказываются значительно |
хуже, |
||||
чем у M-последовательностей |
той же длительности и зависят |
от N0. |
|||
Расчеты на ЭВМ функций |
корреляции сегментов различной дли |
||||
тельности (Na |
= 31, 63, 127, 255, 511) при разных ІѴЭ (m = |
17, 18, 19, |
|||
20) позволили |
определить, что величины иб м а к с у 90% сегментов не |
||||
превосходит |
уровня 3]/"іѴс , |
а у 5 0 % — у р о в н я |
2 ] / і Ѵ с ; |
при этом |
|
вероятность появления u g макс указанных уровней |
в апериодическом |
||||
режиме меньше, чем в периодическом. В случае необходимости иметь величину «б м а к с , не превосходящую определенный уровень, сущест-
5 Зак. 1302 |
129 |
