
Курс_ТОЭ-1_2011_12
.pdf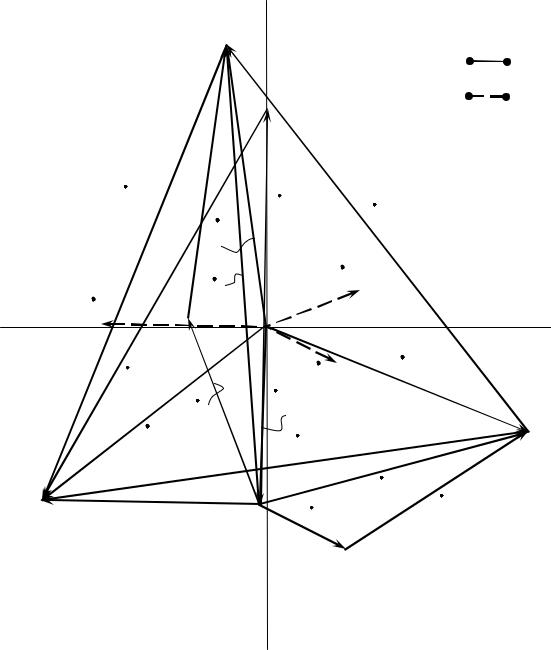
+
А'
25 кВ
1 кА
C
|
UC′A′ |
|
UCN |
UА′В′ |
|
|
|
||
|
|
EэА |
|
|
|
|
|
|
|
|
|
UА′n |
|
IА |
IС |
|
|
|
|
A |
|
N |
|
|
+j |
|
|
|
|
|
UC′C |
|
IВ |
EэВ |
|
|
|
||
|
|
UAn |
UnN |
|
|
|
|
|
|
|
EэС |
|
UВ′C′ |
B' |
|
|
|
|
|
|
|
|
|
UB′n |
C' |
|
n |
UВn |
UB′В |
|
|
|||
|
|
|
|
B |
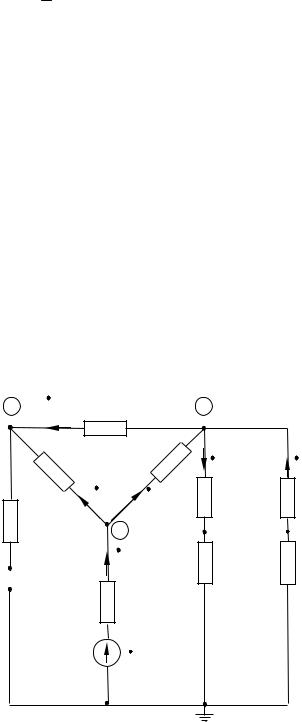
Рис. 2.24. Векторная диаграмма токов и топографическая диаграмма напряжений несимметричной трехфазной цепи
43
Погрешность вычислений составляет:
|Рист − Рпотр| |
|1155,05 − 1155,046| |
|||||||
εР = |
100 % = |
|
100 % = 0,0003463%; |
|||||
|
|
Рист |
|
1155,05 |
|
|
||
|
Qист − Qпотр |
|
1045,68 − 1045,6812 |
|
|
|||
|
|
|
||||||
εQ = |
|
|
100 % = |
|
1045,68 |
|
100% = 0,0001148 %. |
|
Qист |
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
||||
Погрешность не выше допустимой 0,1 %.
Для измерения активной мощности в трехфазной трехпроводной цепи (как в нашем случае на рис. 2.9) может быть применена схема включения двух ваттметров (схема Арона), изображенная на рис. 2.25.
|
|
* |
|
|
А′ |
* |
W1 |
|
IA |
|
|
|||
|
|
|
* |
|
В′ |
|
* |
W2 |
IB |
|
|
С′ 

 IC
IC
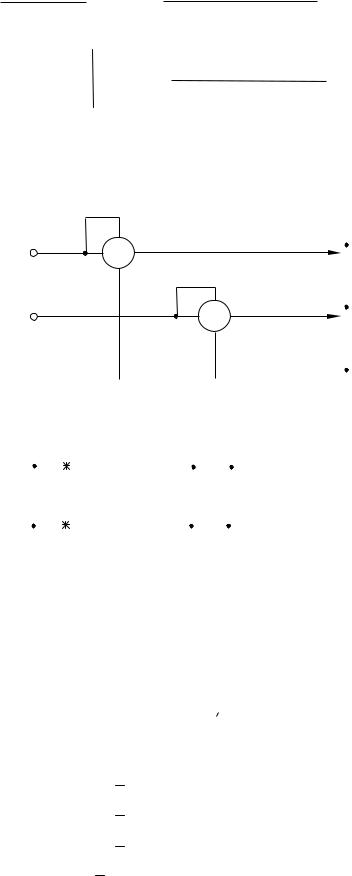
Рис. 2.25. Схема включения ваттметров
Рассчитаем показания ваттметров:
Р1 = Re(UA′C′IA) = UA′C′IAcos(UA′C′^IA) = 326,27 2,673 cos(−21,54° + 68,44°) =
= 595,85 МВт;
Р2 = Re(UВ′C′IВ) = UВ′C′IВcos(UВ′C′^IВ) = 326,27 2,1235 cos(−81,54° + 117,7°) =
= 559,2 МВт.
Сумма показаний двух ваттметров, включенных по схеме рис. 2.25, определяет активную мощность всей трехфазной цепи
Р1 + Р2 = 595,85 + 559,2 = 1155,05 МВт.
Полученный результат соответствует рассчитанным ранее Рпотр и
Рист.
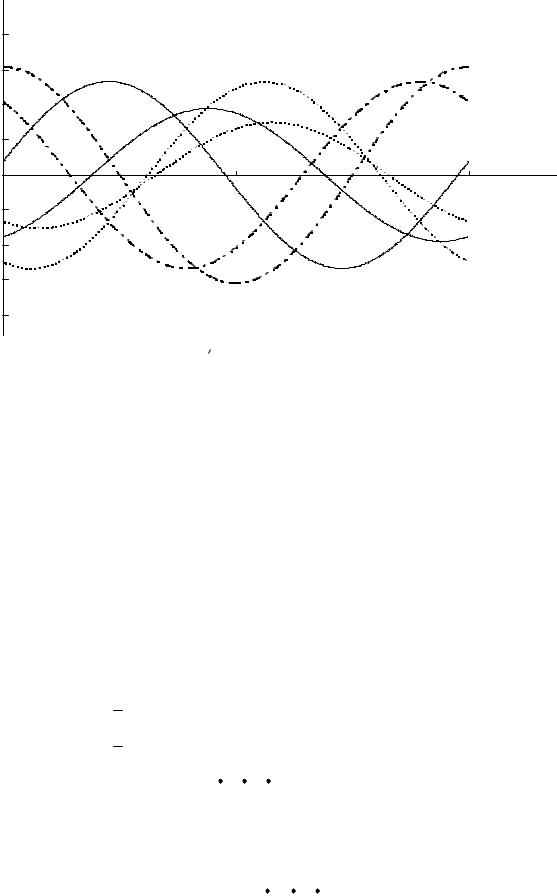
Построим графики временных зависимостей еэА(t), eэВ(t), eэС(t), iA(t), iB(t), iC(t) (рис. 2.26), для чего произведем расчет мгновенных значений величин (табл. 2.10):
eэА = 188,37√2sin(314t + 8,46°) кВ; eэВ = 188,37√2sin(314t − 111,54°) кВ; eэС = 188,37√2sin(314t + 128,46°) кВ; iA = 2,673√2sin(314t − 68,44°) кА;
44
e, кВ |
i, кА |
|
|
400 |
8 |
|
|
300 |
6 |
|
еэА |
200 |
4 |
|
|
100 |
2 |
iC |
iA |
0 |
|
|
|
-100 |
-2 |
|
|
-200 |
-4 |
|
|
-300 |
-6 |
|
|
-400 |
-8 |
|
|
еэВ |
еэС |
iB
π |
2π ω t, рад. |
Рис. 2.26. Графики временных зависимостей
Таблица 2.10. Результаты расчета мгновенных значений величин
ωt |
еэА |
еэВ |
еэС |
iA |
iB |
iC |
град. |
кВ |
кВ |
кВ |
кА |
кА |
кА |
0 |
39,192 |
-247,79 |
208,6 |
-3,5157 |
-2,6582 |
6,1733 |
30 |
165,69 |
-263,5 |
97,81 |
-2,3501 |
-3,0007 |
5,35 |
60 |
247,79 |
-208,6 |
-39,192 |
-0,5548 |
-2,5392 |
3,0932 |
90 |
263,5 |
-97,81 |
-165,69 |
1,3891 |
-1,3974 |
0,00754 |
120 |
208,6 |
39,192 |
-247,79 |
2,9609 |
0,11895 |
-3,0801 |
150 |
97,81 |
165,69 |
-263,5 |
3,7393 |
1,6034 |
-5,3425 |
180 |
-39,192 |
247,79 |
-208,6 |
3,5157 |
2,6582 |
-6,1733 |
210 |
-165,69 |
263,5 |
-97,81 |
2,3501 |
3,0007 |
-5,35 |
240 |
-247,79 |
208,6 |
39,192 |
0,5548 |
2,5392 |
-3,0932 |
270 |
-263,5 |
97,81 |
165,69 |
-1,3891 |
1,3974 |
-0,00754 |
300 |
-208,6 |
-39,192 |
247,79 |
-2,9609 |
-0,11895 |
3,0801 |
330 |
-97,81 |
-165,69 |
263,5 |
-3,7393 |
-1,6034 |
5,3425 |
360 |
39,192 |
-247,79 |
208,6 |
-3,5157 |
-2,6582 |
6,1733 |
iВ = 2,1235√2sin(314t − 117,73°) кА; iС = 4,3652√2sin(314t + 89,93°) кА.
6.В схеме рис. 2.9 токи IA, IB, IC образуют несимметричную систему
исодержат поэтому кроме токов прямой последовательности также составляющие обратной последовательности (токи нулевой последовательности в данном случае отсутствуют, так как нейтральная точка несимметричного приемника изолирована).
Выполним разложение токов IA, IB, IC на симметричные составляю-
щие.
Составляющие прямой последовательности:
45
I1A = (IA + aIB + a2IC)/3 = (2,6726e-j68,44° + a2,1235e-j117,73° + +a24,3652ej89,93°)/3 = 2,2939 − j1,5296 = 2,7571e-j33,7° кА; I1B = a2I1A = 2,7571e-j153,7° кА;
I1C = aI1A = 2,7571ej86,3° кА.
Составляющие обратной последовательности:
I2A = (IA + a2IB + aIC)/3 = (2,6726e-j68,44° + a22,1235e-j117,73° + a4,3652ej89,93°)/3= = −1,3116 − j0,9559 = 1,623e-j143,91° кА;
I2B = aI2A = 1,623e-j23,91° кА; I2C = a2I2A = 1,623ej96,09° кА.
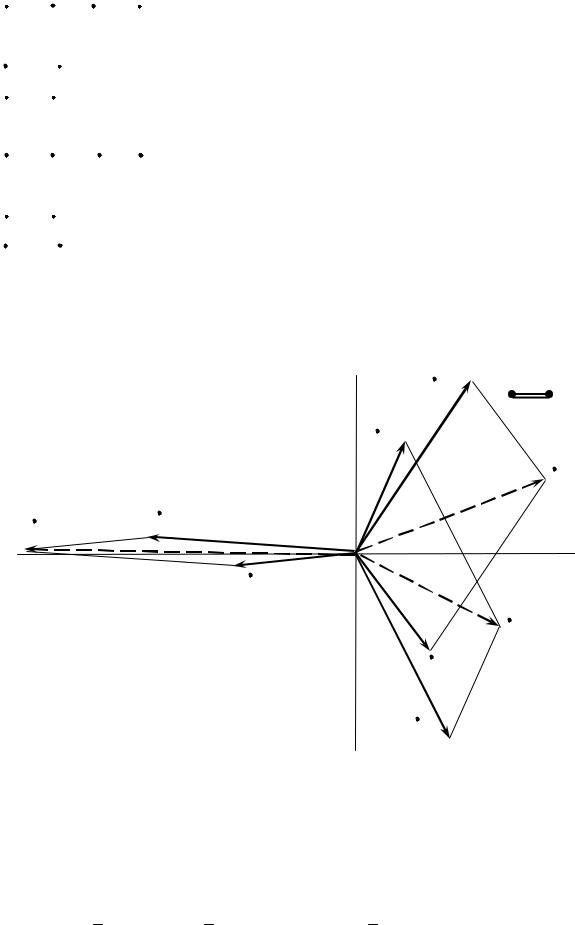
На рис. 2.27 представлена векторная диаграмма токов и их симметричных составляющих. Пунктиром показано векторное суммирование составляющих и возврат к исходной несимметричной системе токов для проверки расчетов.
+ |
I1А |
0,5 кА |
I2В
IА
IС |
I1С |
|
|
||
+j |
0 |
|
I2С |
||
|
IВ
I2А
I1В
Рис. 2.27. Симметричные составляющие токов
7. Далее рассматривается режим работы симметричной трехфазной цепи (см. п.1 и рис. 2.21) в случае, когда в ЭДС одного из генераторов (допустим, первого) появились кроме первой (основной, ранее рассмотренной) высшие гармоники, и теперь е1(t) фазы А определяется выражением
е1(t) = 220√2sin(ωt) + 44√2sin(3ωt + π/3) + 22√2sin(5ωt + 5π/6) кВ,
46
т.е. дополнительно учитываются третья и пятая гармоники с угловыми частотами соответственно ω3 = 3ω = 942 рад/с и ω5 = 5ω = 1570 рад/с.
При этом ЭДС другого генератора остается по-прежнему синусоидальной и для фазы А равной:
е2(t) = 220√2sin(ωt + π/4) кВ.
Расчет ведется для цепи, изображенной на рис. 2.21 без учета несимметричной нагрузки, т.е. для симметричного режима, что позволяет вести расчет на одну фазу (фазу А). Причем, расчет для основной гармоники выполнен ранее в части 1 работы.
Рассчитаем цепь рис. 2.21 для третьей гармоники, составив предварительно расчетную схему замещения на одну фазу (рис. 2.28).
Учтем при этом, что ЭДС третьей гармоники второго генератора равна нулю, нейтральные точки N1, N2 и n2 заземлены через сопротивления, указанные в табл. 2.6 и пересчитанные для третьей гармоники, нейтральная точка n1 изолирована.
Третья гармоника, как известно, образует в трехфазной системе нулевую последовательность чередования фаз, а в участках нейтрального провода при этом протекают утроенные фазные токи нулевой последовательности. В связи, с чем сопротивления заземлений в однофазной схеме рис. 2.28 утраиваются.
1 I3(3) |
Z3(3) |
|
3 |
|
|
Z5(3) Z4(3) |
I7 (3) |
I2(3) |
|
|
I5(3) |
I4(3) |
Z7(3) |
Z2(3) |
Z6(3) |
2 |
|
n2 |
N2 |
n1 |
I1(3) |
|
3Zn2(3) |
3ZN2(3) |
|
Z1(3) |
|
|
|
E1(3)
N1
Рис. 2.28. Расчетная схема на одну фазу для третьей гармоники
Поскольку в соответствии с заданием ток рассчитывается только в ветви с несинусоидальным источником е1(t), преобразуем схему рис. 2.28 к виду рис. 2.29.
Рассчитаем сопротивления ветвей для тока третьей гармоники:
47

Z1(3) I1(3) |
2 |
|
|
|
|
E1(3) Zэ(3)
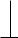 N1
N1
Рис. 2.29. Преобразованная схема
Z1(3) = R1 + j3X1 = 15 + j3 46 = 15 + j138 Ом;
Z2(3) = R2 + j3X2 = 50 + j3 110 = 50 + j330 Ом;
Z3(3) = R3 + j3X3 = 30 + j3 70 = 30 + j210 Ом;
Z4(3) = R4 + j3X4 = 36 + j3 60 = 3 6+ j180 Ом;
Z5(3) = R5 + j3X5 = 40 + j3 66 = 40 + j198 Ом;
Z6(3) = R6 + j3X6 = 600 + j3 400 = 600 + j1200 Ом;
Z7(3) = R7 − jX7/3 = 600 − j300/3 = 600 − j100 Ом.
В дальнейшем учтем, что в шестой ветви для тока третьей гармоники имеется разрыв (n1 изолирована от заземленной точки).
Учитывая, что в табл. 2.6 ZN2 и Zn2 заданы для первой гармоники, получим:
ZN2(3) = 3 j8 = j24 Ом; |
Zn2(3) = 3 j5 = j15 Ом. |
Определяем эквивалентное сопротивление Zэ(3) (см. рис. 2.29), для чего преобразуем схему рис. 2.28.
|
Z4(3)(Z3(3) + Z5(3)) |
(Z7(3) + 3Zn2(3))(Z2(3) + 3ZN2(3)) |
||
Zэ(3)= |
|
|
+ |
= 238,68 + j377,1 Ом. |
|
||||
|
|
Z4(3) + Z3(3) + Z5(3) |
Z7(3) + 3Zn2(3) + Z2(3) + 3ZN2(3) |
|
Ток третьей гармоники в ветви с источником е1 будет:
I1(3) = E1(3)/(Z1(3) + Zэ(3)) = 44ej60°/(15 + j138 + 238,68 + j377,1) = 0,076465 − − j0,005052 = 0,07663e-j3,78° кА;
i1(3 )= √2 0,07663sin(3ωt − 3,78°) кА.
Переходим к расчету цепи рис. 2.21 для пятой гармоники при
е1(5) = 22√2sin(5ωt + 5π/6) кВ.
Расчетная схема на одну фазу приведена на рис. 2.30. Токи пятой гармоники образуют в трехфазных цепях симметричные системы обратной последовательности, поэтому во всех нейтральных проводах токи равны нулю, а потенциалы всех нейтральных точек одинаковы, и на рис. 2.21 и 2.30 эти точки объединены.
Определяем сопротивления ветвей для тока пятой гармоники:
48
1 |
I3(5) Z3(5) |
|
3 |
|
|
Z5(5) Z4(5) |
|
I7 (5) |
I2(5) |
|
I5(5) |
I4(5) |
Z7(5) |
Z2(5) |
Z6(5) |
2 |
|
|
|
|
I1(5) |
|
|
|
I6(5) |
Z1(5) |
|
|
|
E1(5)
n1 |
N1 |
n2 |
N2 |
Рис. 2.30. Расчетная схема для пятой гармоники
Z1(5) = R1 + j5X1 = 15 + j5 46 = 15 + j230 Ом;
Z2(5) = R2 + j5X2 = 50 + j5 110 = 50 + j550 Ом;
Z3(5) = R3 + j5X3 = 30 + j5 70 = 30 + j350 Ом;
Z4(5) = R4 + j5X4 = 36 + j5 60 = 36 + j300 Ом;
Z5(5) = R5 + j5X5 = 40 + j5 66 = 40 + j330 Ом;
Z6(5) = R6 + j5X6 = 600 + j5 400 = 600 + j2000 Ом;
Z7(5) = R7 − jX7/5 = 600 − j300/5 = 600 − j60 Ом.
Рассчитываем Zэ(5) (рис. 2.31), для чего преобразуем треугольник сопротивлений Z3(5), Z4(5), Z5(5) в эквивалентную звезду, объединяем последовательно и параллельно соединенные элементы.
Z1(5) I1(5) |
2 |
|
|
|
|
E1(5) Zэ(5)
 N1
N1
Рис. 2.31. Преобразованная расчетная схема для пятой гармоники
Z35(5) = Z3(5)Z5(5)/(Z3(5) + Z4(5) + Z5(5)) = 11,6363 + j117,891 Ом;
Z45(5) = Z4(5)Z5(5)/(Z3(5) + Z4(5) + Z5(5)) = 13,442 + j101,005 Ом; Z34(5) = Z3(5)Z4(5)/(Z3(5) + Z4(5) + Z5(5)) = 10,449 + j107,171 Ом;
Z27(5) = Z2(5)Z7(5)/(Z2(5) + Z7(5)) = 303,622 + j274,193 Ом;
49

Zэ(5) = Z45(5) + (Z35(5) + Z6(5))(Z34(5) + Z27(5))/(Z35(5) + Z6(5) + Z34(5) + Z27(5)) =
= 249,33 + j434,68 Ом.
Ток пятой гармоники в ветви с источником е1 будет:
I1(5) = E1(5)/(Z1(5) + Zэ(5)) = 22ej150°/(15 + j230 + 249,33 + j434,68) = 0,004447 + + j0,030433 = 0,03076ej81,69° кА;
i1(5) = 0,03076√2sin(5ωt + 81,69°) кА.
Применяя метод наложения, запишем токи в фазах генератора Г1:
i1A = i1(1) + i1(3) + i1(5) = 0,5935√2sin(314t − 115,23°) + 0,07663√2sin(3 314t −
− 3,78°) + 0,03076√2sin(5 314t + 81,69°) кА;
i1В = 0,5935√2sin(314t − 235,23°) + 0,07663√2sin(3 314t −3,78°) + + 0,03076√2sin(5 314t + 201,69°) кА;
i1С = 0,5935√2sin(314t + 4,77°) + 0,07663√2sin(3 314t −3,78°) + + 0,03076√2sin(5 314t − 38,31°) кА.
Обратим внимание, что в отличие от токов первой гармоники, образующих прямую последовательность, токи третьей гармоники в фазах А, В и С генератора имеют одинаковые начальные фазы, а токи пятой гармоники имеют обратный порядок чередования фаз.
Для построения несинусоидальных функций ЭДС генератора Г1 и тока в фазе А составим табл. 2.11, в которой мгновенные значения величин даны для интервала времени, равного одному периоду каждой гармоники.
Таблица 2.11. Результаты расчета мгновенных значений гармоник ЭДС е1(t) и тока i1(t)
кωt, |
e1(1), |
e1(3), |
e1(5), |
i1(1), |
i1(3), |
i1(5), |
град |
кВ |
кВ |
кВ |
кА |
кА |
кА |
0 |
0 |
53,889 |
15,556 |
-0,75927 |
-0,0071444 |
0,043044 |
30 |
155,56 |
62,225 |
0 |
-0,83643 |
0,04788 |
0,040421 |
60 |
269,44 |
53,889 |
-15,556 |
-0,68947 |
0,090076 |
0,026967 |
90 |
311,13 |
31,113 |
-26,944 |
-0,35777 |
0,108135 |
0,0062871 |
120 |
269,44 |
0 |
-31,113 |
0,069796 |
0,09722 |
-0,016077 |
150 |
155,56 |
-31,113 |
-26,944 |
0,47866 |
0,060255 |
-0,034134 |
180 |
0 |
-53,889 |
-15,556 |
0,75927 |
0,0071444 |
-0,043044 |
210 |
-155,56 |
-62,225 |
0 |
0,83643 |
-0,04788 |
-0,040421 |
240 |
-269,44 |
-53,889 |
15,556 |
0,68947 |
-0,090076 |
-0,026967 |
270 |
-311,13 |
-31,113 |
26,944 |
0,35777 |
-0,108135 |
-0,0062871 |
300 |
-269,44 |
0 |
31,113 |
-0,069796 |
-0,09722 |
0,016077 |
330 |
-155,56 |
31,113 |
26,944 |
-0,47866 |
-0,060255 |
0,034134 |
360 |
0 |
53,889 |
15,556 |
-0,75927 |
-0,0071444 |
0,043044 |
50

е1(t) = 220√2sin(ωt) + 44√2sin(3ωt + π/3) + 22√2sin(5ωt + 5π/6) кВ; i1(t) = 0,5935√2sin(ωt − 115,23°) + 0,07663√2sin(3ωt − 3,78°) +
+ 0,03076√2sin(5ωt + 81,69°) кА
При построении временных зависимостей (рис. 2.32 и рис. 2.33) необходимо учесть, что период третьей гармоники будет определяться на оси времени t в три раза меньшим отрезком, чем период первой гармоники (для пятой гармоники − в пять).
Расчетные мгновенные значения несинусоидальных ЭДС е1(t) и тока i1(t) приведены в табл. 2.12, а графики временных зависимостей указанных величин на рис.2.32 и 2.33.
Таблица 2.12. Результаты расчета мгновенных значений несинусоидальных ЭДС е1(t) и тока i1(t)
ωt, град. |
t, с |
e1(t), кВ |
i1(t), кА |
0 |
0 |
69,445 |
-0,72378 |
10 |
0,000555 |
105,611 |
-0,7295 |
20 |
0,00111 |
131,064 |
-0,7470 |
30 |
0,001667 |
159,732 |
-0,7624 |
40 |
0,00222 |
194,586 |
-0,757 |
50 |
0,002778 |
227,223 |
-0,7225 |
60 |
0,00333 |
246,668 |
-0,6662 |
70 |
0,00389 |
250,137 |
-0,6025 |
80 |
0,00444 |
247,109 |
-0,5372 |
90 |
0,005 |
253,07 |
-0,4596 |
100 |
0,00555 |
277,164 |
-0,3466 |
110 |
0,0061 |
312,835 |
-0,18025 |
120 |
0,00667 |
338,889 |
0,0357 |
130 |
0,00722 |
331,203 |
0,2707 |
140 |
0,00778 |
277,711 |
0,48 |
150 |
0,00833 |
186,676 |
0,6272 |
160 |
0,00889 |
82,578 |
0,702 |
170 |
0,00944 |
-7,726 |
0,72301 |
180 |
0,01 |
-69,445 |
0,72378 |
Действующие значения несинусоидальных величин ЭДС и тока определяются по формулам:
Е1 = √Е1(1)2 + Е1(3)2 + Е1(5)2 = √2202 + 442 + 222 = 225,433 кВ;
I1 = √I1(1)2 + I1(3)2 + I1(5)2 = √0,59352 + 0,076632 + 0,030762 = 0,5992 кА.
51
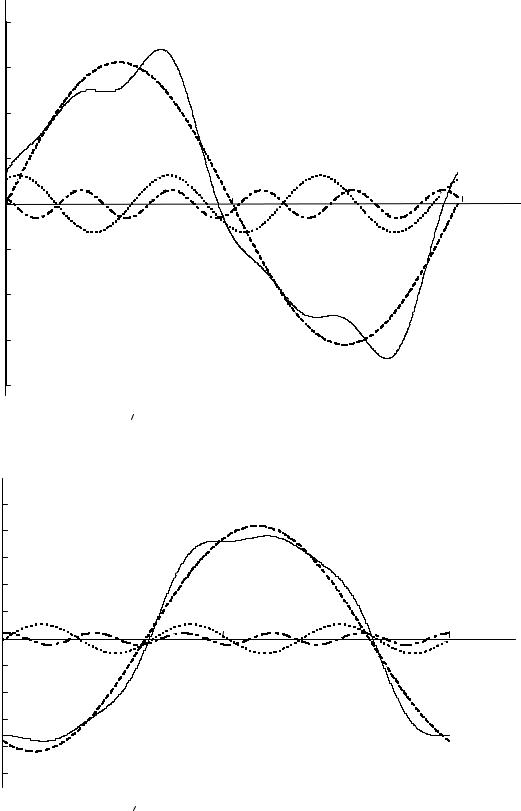
e, кВ |
|
|
|
400 |
|
|
|
|
е1(1) |
е1 |
|
300 |
|
|
|
|
|
|
|
200 |
|
|
|
100 |
е1(5) |
е1(3) |
|
|
|
|
|
0 |
|
π |
2π ωt, рад. |
|
|
||
-100 |
|
|
|
-200 |
|
|
|
-300 |
|
|
|
-400 |
|
|
|
Рис. 2.32. Временная зависимость е1(t) |
|
||
i, кА |
|
|
|
1 |
i1 |
i1(1) |
|
0,8 |
|
||
0,6 |
|
|
|
0,4 |
i1(3) i1(5) |
|
|
0,2 |
|
||
0 |
π |
2π ωt, рад. |
|
-0,2 |
|||
|
|
||
-0,4 |
|
|
|
-0,6 |
|
|
|
-0,8 |
|
|
|
-1 |
|
|
Рис. 2.33. Временная зависимость i1(t)
52
