
Курс_ТОЭ-1_2011_12
.pdf
Уравнения по методу контурных токов при наличии индуктивной связи будут иметь вид:
I11(Z3 + Z4 + Z5 ± 2ZM) + I22(−Z5) + I33(Z4 ± ZM)+I44(−Z4 ± ZM) = 0; I11(−Z5) + I22(Z1 + Z5 + Z6) + I33(Z1) + I44(−Z1) = E1;
I11(Z4 ± ZM) + I22(Z1) + I33(Z1 + Z4 + Z7) + I44(−Z1 − Z4) = E1;
I11(−Z4 ± ZM) + I22(−Z1) + I33(−Z1 − Z4) + I44(Z1 + Z4 + Z2) = E2 − E1.
Верхний знак перед сопротивлением взаимной индукции соответствует согласному действию токов индуктивно связанных ветвей, нижний знак − встречному.
2.3. Порядок выполнения части 2
Расчет трехфазных электрических цепей
В части 2 рассматривается трехфазная цепь, симметричный режим работы которой рассчитывался на одну фазу в части 1.
Первый уровень сложности Несимметричный режим в нестатической цепи
(применение метода симметричных составляющих)
1.Начертить схему трехфазной цепи в развернутом виде с отражением в ней места несимметрии, вида несимметрии и режимов работы нейтралей в соответствии с вариантом задания (табл. 2.4).
2.Построить векторную диаграмму симметричной трехфазной системы токов ветви, связывающей указанный в табл. 2.4 узел с землей или нейтральной точкой. Для этой же ветви построить топографическую диаграмму напряжений, определить фазные и линейные напряжения в указанной узловой точке.
3.Записать для симметричного режима мгновенные значения фазных токов и напряжений указанной ветви. Построить графики их временных зависимостей.
4.Для расчета несимметричного режима составить схемы замещения прямой, обратной, нулевой последовательностей и рассчитать параметры ветвей для токов обратной и нулевой последовательностей.
5.Преобразовать схемы прямой, обратной, нулевой последовательностей по теореме об активном двухполюснике относительно участка несимметрии.
23

Таблица 2.4. Исходные данные для расчета несимметричного режима трехфазной цепи
варианта |
Место |
|
Режимы работы нейтралей генераторов и нагрузок |
|||||||
несим. |
Вид |
точка |
N1 |
точка |
N2 |
точка |
n1 |
точка |
n2 |
|
|
Г1 |
|
Г2 |
|
Н1 |
|
Н2 |
|
||
|
№ узла |
несимметрии * |
нейтральная |
нейтральная |
нейтральная |
нейтральная |
||||
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
2 |
Однофазное |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
||||
|
|
КЗ фазы А |
ZN1 = 0 |
ZN2 = j5 (Ом) |
от земли |
Zn2 = 0 |
|
|||
2 |
3 |
Замыкание на |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
||||
|
|
землю фаз А и В |
ZN1 = j10 (Ом) |
ZN2 = 0 |
Zn1 = j3 (Ом) |
от земли |
||||
3 |
1 |
Однофазное |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
||||
|
|
КЗ фазы В |
ZN1 = 0 |
ZN2 = j8 (Ом) |
от земли |
Zn2 = j5 (Ом) |
||||
4 |
2 |
Замыкание между |
|
|
|
|
|
|
|
|
|
|
фазами А и В (без |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
||||
|
|
касания земли) |
ZN1 = j8 (Ом) |
ZN2 = 0 |
Zn1 = 0 |
|
от земли |
|||
5 |
3 |
Замыкание на |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
||||
|
|
землю фаз В и С |
ZN1 = 0 |
ZN2 = j10 (Ом) |
от земли |
Zn2 = 0 |
|
|||
6 |
1 |
Однофазное |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
||||
|
|
КЗ фазы С |
ZN1 = j6 (Ом) |
ZN2 = 0 |
Zn1 = j5 (Ом) |
от земли |
||||
7 |
2 |
Замыкание на |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
||||
|
|
землю фаз А и С |
ZN1=0 |
|
ZN2 = j12 (Ом) |
от земли |
Zn2=j2 (Ом) |
|||
8 |
3 |
Замыкание между |
|
|
|
|
|
|
|
|
|
|
фазами А и С (без |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
||||
|
|
касания земли) |
ZN1 = j5 (Ом) |
ZN2 = j2 (Ом) |
Zn1 = j2 (Ом) |
от земли |
||||
9 |
1 |
Замыкание между |
|
|
|
|
|
|
|
|
|
|
фазами В и С (без |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
||||
|
|
касания земли) |
ZN1 = 0 |
ZN2 = j6 (Ом) |
от земли |
Zn2 = j4 (Ом) |
||||
10 |
2 |
Однофазное |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
||||
|
|
КЗ фазы С |
ZN1 = j12 (Ом) |
ZN2 = 0 |
Zn1 = j4 (Ом) |
от земли |
||||
Примечание. Реактивные сопротивления генераторов для токов обратной последовательности уменьшить в 4 раза, нулевой − в 10 раз.
Сопротивления линий для токов обратной последовательности оставить равными сопротивлениям прямой последовательности, а для нулевой последовательности увеличить в 3,5 раза реактивную составляющую.
Модули реактивных сопротивлений нагрузки для токов обратной последовательности уменьшить в 5 раз, а для нулевой последовательности - в 10 раз.
* По усмотрению преподавателя могут быть предложены для расчета другие виды несимметрии, например обрывы в различных фазах ЛЭП.
6.Записать систему уравнений для расчета симметричных составляющих токов и напряжений (три уравнения активного двухполюсника и три дополнительных, определяющих вид несимметрии).
7.Решить систему уравнений, определить симметричные составляющие токов и напряжений.
8.Определить токи и напряжения несимметричного участка трехфазной цепи. Построить их на одной диаграмме с симметричным режимом.
24

9. Найти токи в ветви, указанной в п.2, сопоставить их с токами симметричного режима и так же изобразить их на векторной диаграмме.
Второй уровень сложности
Несимметричный режим в статической цепи
1.Начертить схему симметричной трехфазной цепи в развернутом виде. Записать в комплексной форме системы ЭДС симметричных трехфазных генераторов и токов в них.
2.Дополнить схему трехфазной цепи статической (не содержащей вращающихся машин и имеющей параметры, не зависящие от степени несимметрии токов) несимметричной нагрузкой, подключаемой к одному из узлов схемы в соответствии с вариантом задания (табл. 2.5). Нейтраль несимметричной нагрузки не заземлена и не имеет соединения с нейтральными точками генераторов. Режимы работы нейтралей генераторов
исимметричных нагрузок указаны в табл. 2.6.
3.Построить для симметричного трехфазного режима топографическую диаграмму напряжений и векторную диаграмму токов, используя результаты расчета в части 1. На топографической диаграмме показать только потенциалы узловых точек и ЭДС генераторов, токи указать только в ветвях с источниками энергии.
4.По теореме об активном двухполюснике всю симметричную часть цепи заменить относительно зажимов подключения несимметричной нагрузки эквивалентным трехфазным генератором. Определить параметры последовательной схемы замещения эквивалентного генератора Uxx и Zвх, полагая сопротивления всех ветвей цепи неизменными при нарушении симметрии (свойство статической цепи). Привести схему к виду рис. 2.9.
Таблица 2.5. Параметры несимметричной статической нагрузки
№ |
Место несим. |
Параметры несимметричной нагрузки |
|
||
вар. |
Номер узла |
ZА |
ZB |
ZC |
Примечание |
1 |
3 |
j600 |
−j300 |
300 |
Нейтраль не- |
2 |
2 |
j100 |
j200 |
j100 |
симметричной |
3 |
3 |
400 |
j400 |
−j400 |
нагрузки изоли- |
4 |
1 |
−j400 |
j400 |
400 |
рована от земли |
5 |
2 |
80 |
j80 |
−j80 |
|
6 |
1 |
−j200 |
200 |
j100 |
|
7 |
2 |
200 − j200 |
200 |
j200 |
|
8 |
3 |
j800 |
800 |
80 + j800 |
|
9 |
3 |
1500 |
j1500 |
−j1500 |
|
10 |
1 |
−j500 |
j250 |
300 |
|
25
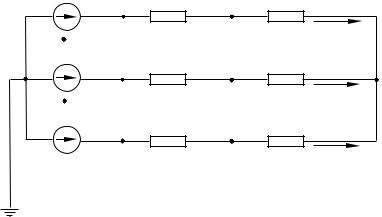
Таблица 2.6 .Режимы работы нейтралей генераторов и нагрузок
№ |
Место |
Нейтральная точ- |
Нейтральная точ- |
Нейтральная точ- |
Нейтральная точ- |
вар. |
несим. |
ка N2 (первого |
ка N2 (второго |
ка n1 (первого |
ка n2 (второго |
|
(№ узла) |
генератора) |
генератора) |
приемника) |
приемника) |
1 |
2 |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
|
|
ZN1 = 0 |
ZN2 = j5 (Ом) |
от земли |
Zn2 = 0 |
2 |
3 |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
|
|
ZN1 = j10 (Ом) |
ZN2 = 0 |
Zn1 = j3 (Ом) |
от земли |
3 |
1 |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
|
|
ZN1 = 0 |
ZN2 = j8 (Ом) |
от земли |
Zn2 = j5 (Ом) |
4 |
2 |
|
|
|
|
|
|
Заземлена |
Заземлена |
Заземлена |
Изолирована |
|
|
ZN1 = j8 (Ом) |
ZN2 = 0 |
Zn1 = 0 |
от земли |
5 |
3 |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
|
|
ZN1 = 0 |
ZN2 = j10 (Ом) |
от земли |
Zn2 = 0 |
6 |
1 |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
|
|
ZN1 = j6 (Ом) |
ZN2 = 0 |
Zn1 = j5 (Ом) |
от земли |
7 |
2 |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
|
|
ZN1 = 0 |
ZN2 = j12 (Ом) |
от земли |
Zn2 = j2 (Ом) |
8 |
3 |
|
|
|
|
|
|
Заземлена |
Заземлена |
Заземлена |
Изолирована |
|
|
ZN1 = j5 (Ом) |
ZN2 = j2 (Ом) |
Zn1 = j2 (Ом) |
от земли |
9 |
1 |
|
|
|
|
|
|
Заземлена |
Заземлена |
Изолирована |
Заземлена |
|
|
ZN1 = 0 |
ZN2 = j6 (Ом) |
от земли |
Zn2 = j4 (Ом) |
10 |
2 |
Заземлена |
Заземлена |
Заземлена |
Изолирована |
|
|
ZN1 = j12 (Ом) |
ZN2 = 0 |
Zn1 = j4 (Ом) |
то земли |
5. Для схемы рис. 2.9 выполнить следующее: а) рассчитать напряжение смещения нейтрали; б) найти токи в несимметричной нагрузке;
в) построить векторную диаграмму токов и топографическую диаграмму напряжений;
г) сделать проверку расчета по уравнениям баланса мощностей;
ЕЭА = Uxx |
Zвх |
|
ZA |
|
A′ |
A |
iA(t ) |
EЭВ |
Zвх |
|
ZB |
|
|
|
n |
N |
B′ |
B |
iB(t ) |
ЕЭС |
Zвх |
|
ZC |
|
C′ |
C |
iC(t) |
Рис. 2.9. Эквивалентная расчетная схема
26

д) включить ваттметры для измерения активной мощности несимметричного приемника и рассчитать их показания;
е) построить графики временных зависимостей iA(t), iB(t), iC(t), еЭА(t), еЭВ(t), еЭС(t).
6.Разложить на симметричные составляющие систему линейных токов схемы рис. 2.9. Построить их векторные диаграммы.
7.В симметричной трехфазной цепи (п.1) один из источников (табл. 2.7) генерирует ЭДС, содержащую кроме основной, рассмотренной ранее (п.1, 2), также высшие гармоники с параметрами, указанными в табл. 2.7.
Таблица 2.7. Исходные данные для расчета цепи несинусоидального тока
|
|
|
Параметры несинусоидальной ЭДС фазы А |
|
|||
№ |
Номер |
е(t) = Em(1)sin(ωt + ψ(1)) + Em(3)sin(ωt + ψ(3)) + Em(5)sin(ωt + ψ(5)) |
|||||
вар. |
источника |
n3 |
|
ψ(3) |
n5 |
|
ψ(5) |
1 |
1 |
0,25 |
|
180° |
0,1 |
|
0° |
2 |
2 |
0,4 |
|
45° |
0,2 |
|
75° |
3 |
1 |
0,3 |
|
75° |
0,15 |
|
135° |
4 |
2 |
0,35 |
|
15° |
0,23 |
|
45° |
5 |
1 |
0,45 |
|
25° |
0,125 |
|
30° |
6 |
2 |
0,2 |
|
30° |
0,3 |
|
150° |
7 |
1 |
0,5 |
|
60° |
0,25 |
|
120° |
8 |
2 |
0,15 |
|
120° |
0,07 |
|
60° |
9 |
1 |
0,23 |
|
90° |
0,12 |
|
90° |
10 |
2 |
0,37 |
|
150° |
0,155 |
|
180° |
Примечание: амплитуда и начальная фаза ЭДС первой гармоники заданы в табл. 1.1;
Em(3) = n3 Em(1); Em(3) = n3 Em(1).
В табл. 2.6 заданы режимы работы нейтралей генераторов и нагрузок, а также параметры заземляющих устройств для первой гармоники.
Для указанного случая выполнить следующее:
а) рассчитать токи в фазах источника с несинусоидальной ЭДС; б) построить несинусоидальные функции заданной ЭДС и найден-
ного тока для фазы А; в) определить их действующие значения.
2.4. Методические указания к части 2
Первый уровень сложности Несимметричный режим в нестатической цепи
(применение метода симметричных составляющих)
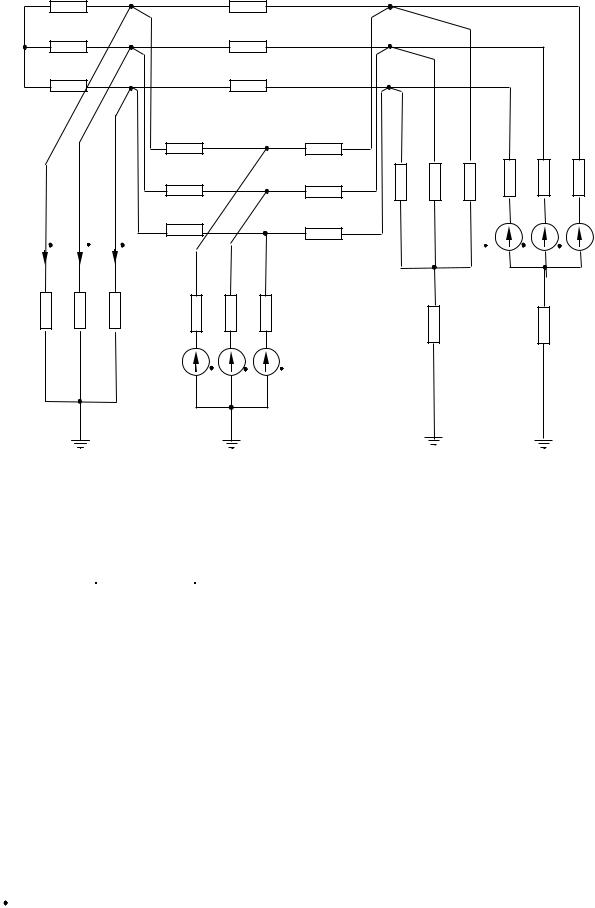
1. На рис. 2.10 представлена трехфазная электрическая цепь рассматриваемого примера.
Вид несимметрии, место несимметрии и режимы работы нейтралей соответствуют в данном примере табл. 2.8.
27
|
Z6 |
1A |
|
Z3 |
|
3A |
|
|
|
|
n1 |
Z6 |
1B |
|
Z3 |
|
3B |
|
|
|
|
|
Z6 |
1C |
|
Z3 |
|
3C |
|
|
|
|
|
|
Z5 |
|
2A |
Z4 |
|
|
|
|
|
|
|
Z5 |
|
2B |
Z4 |
Z7 Z7 |
Z7 |
Z2 |
Z2 |
Z2 |
|
|
Z5 |
|
2C |
Z4 |
|
|
|
|
|
IA |
IB |
IC |
|
|
|
|
|
E2C E2B E2A |
||
|
|
|
|
|
|
|
n2 |
|
|
N2 |
ZA ZB ZC |
Z1 Z1 Z1 |
|
|
Zn2 |
|
|
ZN2 |
|||
|
|
|
E1A |
E1B E1C |
|
|
|
|
|
|
n |
N1 |
Рис. 2.10. Схема трехфазной цепи в развернутом виде
Таблица 2.8. Исходные данные для расчета несимметричного режима трехфазной цепи
Место |
|
Режимы работы нейтралей генераторов и нагрузок |
|||
несимметрии |
Вид |
Г1 |
Г2 |
Н1 |
Н2 |
Номер узла |
несимметрии |
нейтральная |
нейтральная |
нейтральная |
нейтральная |
|
|
точка N1 |
точка N2 |
точка n1 |
точка n2 |
|
Однофазное |
|
|
|
|
1 |
короткое |
Заземлена |
Заземлена |
Изолирована |
Заземлена |
|
замыкание |
ZN1 = 0 |
ZN2 = j8 (Ом) |
от земли |
Zn2 = j5 (Ом) |
|
фазы В |
|
|
|
|
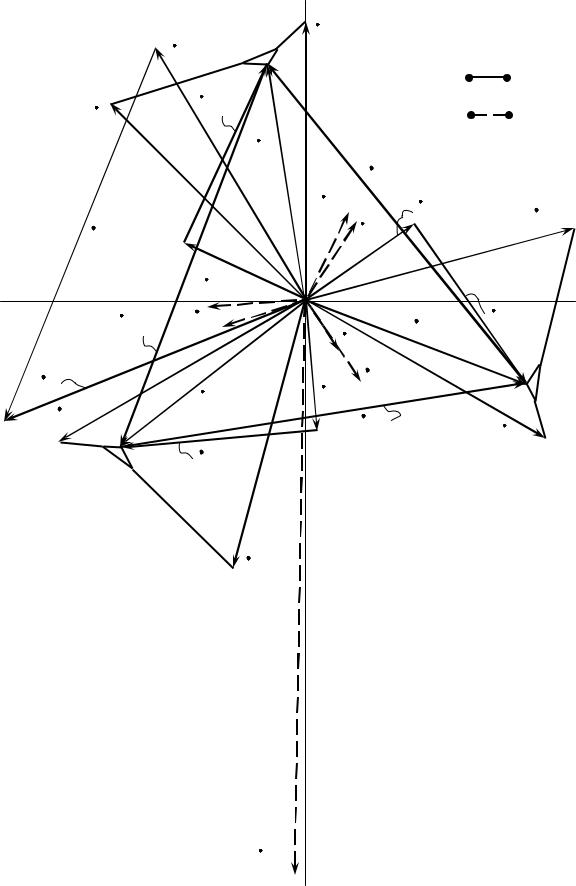
2. С учетом того, что расчетные схемы на одну фазу, как правило, составляются для фазы А, а расчет однофазной схемы выполнен в части 1 работы, строим для симметричного режима трехфазной цепи топографическую диаграмму напряжений и векторную диаграмму токов (рис. 2.11). При построении ограничимся изображением потенциалов только узловых точек, ЭДС генераторов и токов ветви, связывающей заданный узел с нейтральной точкой (в данном случае − ветви 6).
В части 1 расчета было получено значение потенциала ϕ1 = 188,37еj8,46° кВ.
28

Получим фазные и линейные напряжения в указанном узле (узел 1) с помощью соответствующего фазового сдвига и соотношения линейных и фазных напряжений.
Фазные напряжения:
UА10 = 188,37ej8,46° кВ;
UВ10 = 188,37e-j111,54° кВ;
UС10 = 188,37ej128,46° кВ.
Линейные напряжения:
UAB1 = 188,37√3ej38,46° = 326,3ej38,46° кВ;
UBC1 = 188,37√3e-j81,54° = 326,3e-j81,54° кВ;
UCA1 = 188,37√3ej158,46° = 326,3ej158,46° кВ.
3. Запишем мгновенные значения фазных напряжений и токов указанной ветви (ветвь 6).
Фазные напряжения:
uА10 = 188,37√2 sin(ωt + 8,46°) = 266,4sin(ωt + 8,46°) кВ; uВ10 = 188,37√2 sin(ωt − 111,54°) = 266,4sin(ωt − 111,54°) кВ; uС10 = 188,37√2 sin(ωt + 128,46°) = 266,4sin(ωt + 128,46°) кВ.
Фазные токи:
i6A = 0,26√2 sin(ωt − 25,2°) = 0,37 sin(ωt − 25,2°) кА;
i6B = 0,26√2 sin(ωt − 145,2°) = 0,37 sin(ωt − 145,2°) кА; i6C = 0,26√2 sin(ωt + 94,8°) = 0,37 sin(ωt + 94,8°) кА.
Для построения графиков временных зависимостей указанных величин составим таблицу мгновенных значений (табл. 2.9).
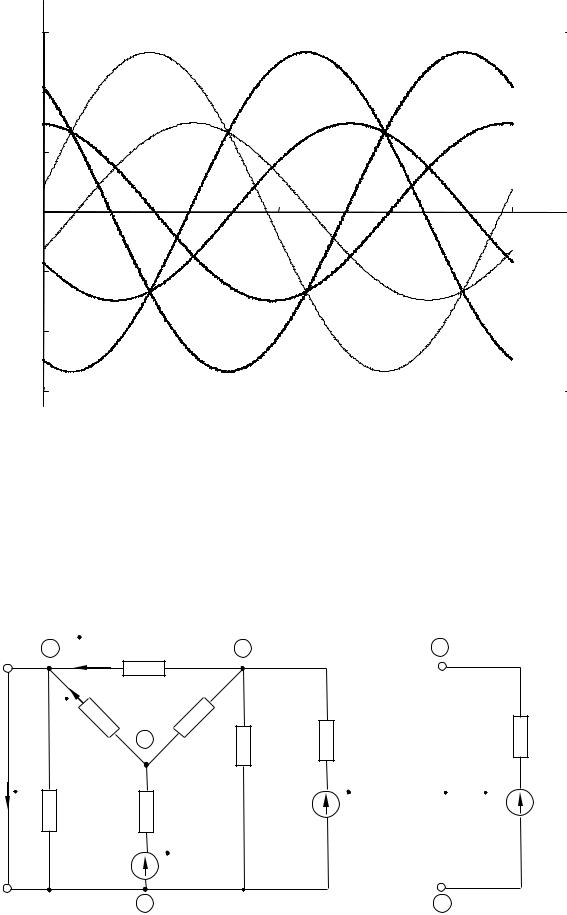
Построенные графики временных зависимостей uA10(t), uB10(t), uC10(t), i6A(t), i6B(t), i6C(t) представлены на рис. 2.12.
Таблица 2.9. Результаты расчета мгновенных значений величин
ωt, град |
0 |
30 |
60 |
90 |
120 |
150 |
180 |
210 |
240 |
270 |
300 |
330 |
uА10, кВ |
39,2 |
165,7 |
247,8 |
263,5 |
208,6 |
97,8 |
-39,2 |
-165,7 |
-247,8 |
-263,5 |
-208,6 |
-97,8 |
uВ10, кВ |
-247,8 |
-263,5 |
-208,6 |
-97,8 |
39,2 |
165,7 |
247,8 |
263,5 |
208,6 |
97,8 |
-39,2 |
-165,7 |
uС10, кВ |
208,6 |
97,8 |
-39,2 |
-165,7 |
-247,8 |
-263,5 |
-208,6 |
-97,8 |
39,2 |
165,7 |
247,8 |
263,5 |
i6A, кА |
-0,158 |
0,031 |
0,211 |
0,335 |
0,369 |
0,304 |
0,158 |
-0,031 |
-0,211 |
-0,335 |
-0,369 |
-0,304 |
i6B, кА |
-0,211 |
-0,335 |
-0,369 |
-0,304 |
-0,158 |
0,031 |
0,211 |
0,335 |
0,369 |
0,304 |
0,158 |
-0,031 |
i6C, кА |
0,369 |
0,304 |
0,158 |
-0,031 |
-0,211 |
-0,335 |
-0,369 |
-0,304 |
-0,158 |
0,031 |
0,211 |
0,335 |
29
|
|
|
+ |
|
|
|
|
|
UА′ |
3A |
2A |
E1А |
|
|
|
|
1A |
|
|
30 кВ |
|
||
|
|
|
|
|
|
||
|
E2А |
URН1А |
|
|
|
0,1 кА |
|
|
|
|
|
|
|
|
|
|
|
|
U1А |
|
|
|
|
|
|
|
|
U1А1В |
|
|
|
|
|
|
|
I6А |
UХН1В |
E2В |
|
|
|
|
|
IА6к |
|||
|
U1С′1А |
|
|
|
|||
|
|
|
|
|
|
||
|
|
I6С |
|
|
|
|
|
+j |
U1С1А |
IС6к |
0 |
|
U1В |
URН1В |
|
|
IВ6к |
|
|||||
|
|
|
|
|
1В |
3В |
|
|
|
|
|
I6В |
|
||
|
UС′ |
|
|
|
|
|
|
|
U1С |
|
UХН1С |
|
|
2В |
|
|
E1С |
|
|
|
|||
|
|
|
U1В1С |
|
|
|
|
|
1С |
|
|
|
E1В |
|
|
|
|
|
|
|
|
||
|
2С |
URН1С |
|
|
|
|
|
|
3С |
|
|
|
|
|
|
|
|
|
E2С |
|
|
|
|
|
|
|
IкзВ |
|
|
|
|
|
Рис. 2.11. Векторная диаграмма токов и топографическая диаграмма |
|
|||||
|
|
напряжений трехфазной цепи |
|
|
|||
30
u, kB i, kA |
|
300 |
0,75 |
200 |
0,5 |
100 |
0,25 |
0 |
|
-100 |
-0,25 |
-200 |
-0,5 |
-300 |
-0,75 |
uA10 |
uB10 |
uC10 |
i6A |
i6B |
i6C |
π |
2π ωt, рад. |
Рис. 2.12. Графики временных зависимостей
4. Для расчета несимметричного режима (однофазное КЗ в фазе В узла 1) составляем схемы замещения прямой, обратной и нулевой последовательностей (рис. 2.13, 2.14, 2.15), которые в дальнейшем (см. п.5) преобразуем по теореме об активном двухполюснике относительно зажимов подключения несимметричной нагрузки.
В соответствии с примечанием к табл. 2.4 пересчитываем сопротивления ветвей для токов обратной Z(2) и нулевой Z(0) последовательностей:
1 I3 |
Z3(1) |
3 |
1 |
I5 |
Z5(1) |
Z4 (1) |
|
|
|
|
|
2 |
Z7(1) |
Z2(1) |
Zвx(1) |
Iкз Z6(1) |
Z1(1) |
E2 |
Eэ(1)=Uxx |
|
E1 |
|
|
|
0 |
|
0 |
Рис. 2.13. Схема замещения прямой последовательности и ее преобразование по теореме об активном двухполюснике
31
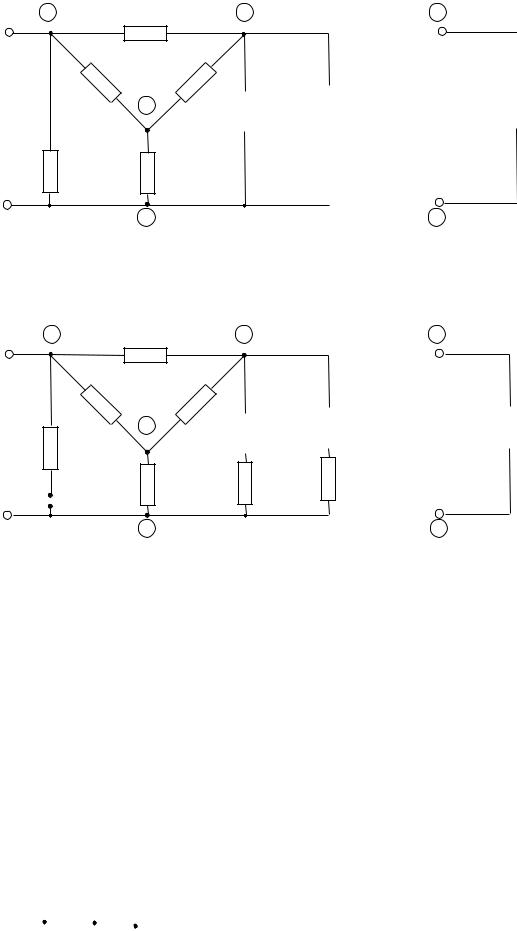
1Z3(2)
Z5(2) Z4 (2)
2 |
Z6(2) Z1(2)
3 |
1 |
|
Z7(2) |
|
|
Z2(2) |
|
|
Z |
вx(2) |
|
|
|
|
|
||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
Рис. 2.14. Схема замещения обратной последовательности и ее преобразование по теореме об активном двухполюснике
1Z3(0)
Z5(0) |
Z4 (0) |
|
2 |
Z6(0 ) |
|
n1 |
Z1(0) |
3 |
1 |
|
Z7(0) |
|
Z2(0) |
|
Zвx(0) |
|
|
|
|||
|
|
|
|
|
|
3Zn2 3ZN2
|
|
|
0 |
|
|
|
0 |
|
Рис. 2.15. Схема замещения нулевой последовательности и ее преобразование |
||||||||
|
|
|
по теореме об активном двухполюснике |
|
||||
Z1(2) = 15 + j34 |
= 37,16ej66,19° Ом; |
Z1(0) = 15 + j106,6 = 107,65ej82° Ом; |
||||||
Z2(2) = 50 |
+ j87,5 = 100,78ej60,26° Ом; |
Z2(0) = 50 |
+ j283 = |
287,4ej80° Ом; |
||||
Z3(2) = 30 |
+ j70 |
= 76,16ej66,8° Ом; |
Z3(0) = 30 |
+ j245 = |
246,8ej83° Ом; |
|||
Z4(2) |
= 36 |
+ j60 |
= 69,97ej59,04° Ом; |
Z4(0) |
= 36 |
+ j210 |
= |
213,06ej80,27° Ом; |
Z5(2) |
= 40 |
+ j66 |
= 77,18ej58,78° Ом; |
Z5(0) |
= 40 |
+ j231 |
= |
234,44ej80,176° Ом; |
Z6(2) |
= 600 + j80 = 605,31ej7,595° Ом; |
Z6(0) |
= 600 + j40 |
= |
601,33ej3,8° Ом; |
|||
Z7(2) |
= 600 − j60 = 603e-j5,71° Ом; |
Z7(0) |
= 600 − j30 |
= 600,75e-j2,86° Ом. |
||||
5. При преобразовании схемы прямой последовательности рис. 2.13 учитываем, что все параметры схемы замещения сохраняют значения, принятые в части 1. Кроме того, в части 1 была определена и эквивалентная ЭДС активного двухполюсника, равная потенциалу узла 1,
Еэ(1) = Uxx = ϕ1 = 188,37ej8,46° кВ.
32
