4.3. Системы нечеткого вывода

Нечеткий вывод занимает центральное место в нечеткой логике. Процесс нечеткого вывода представляет собой некоторую процедуру или алгоритм получения нечетких заключений на основе нечетких условий или предпосылок с использованием рассмотренных в предыдущих пунктах понятий нечеткой логики.

Системы нечеткого вывода являются частным случаем нечетких систем или систем нечетких правил, в которых условия и заключения правил формулируются в форме нечетких лингвистических высказываний относительно тех или иных лингвистических переменных.

Правилом нечеткого вывода или нечетким правилом будем называть выражение следующего вида:

, где - имя нечеткого правила,- сфера применения нечеткого правила,- условие применимости ядра нечеткого правила;- ядро нечеткого правила, в котором(условие ядра),(заключение ядра) - лингвистические высказывания;- метод или способ определения количественного значения степенности истинности заключений ядра;- коэффициент определенности или уверенности нечеткого правила;- постусловия правила.

Сфера применения правил явно или неявно описывает предметную область знания. Условия применимости ядра представляет собой логическое выражение, как правило, предикат. Ядро правила можно записать в более привычной форме ЕСЛИА ТО B или , где- выражения нечеткой логики, которые наиболее часто представляются в форме нечетких высказываний вида (4.33).

- способ или метод определения количественного значения степени истинности заключения на основе значения истинности условия. Данный способ, в общем случае, определяет так называемую схему или алгоритм нечеткого вывода в нечетких системах и называется метод композиции.

- коэффициент определенности или уверенности нечеткого правила выражает количественную оценку степени истинности или относительный вес нечеткого правила. Он принимает значения из интервала и часто называется весовым коэффициентом или весом нечеткого правила.

Наконец постусловие описывает действия или процедуры, которые необходимо выполнить в случае реализации ядра процедуры. Характер этих действий может быть различным и отражать вычислительные или иные аспекты нечеткой системы.

Система нечеткого вывода обычно состоит из следующих пяти блоков.

Рис.4.3. Система нечеткого вывода

Для получения заключений в системах нечеткого существует ряд алгоритмов вывода, описание которых базируется на разделении процесса вывода на ряд последовательных этапов:

1. Формирование базы правил систем нечеткого вывода;

2. Фаззификация входных переменных;

3. Агрегирование подусловий в нечетких правилах продукций;

4. Активация или композиция подзаключений в нечетких правилах продукций;

5. Аккумулирование заключений нечетких правил продукций.

Рассмотрим основные особенности каждого из этапов.

Формирование базы правил систем нечеткого вывода.

База правил {R_i}^k_i=1 системы нечеткого вывода предназначена для формального представления эмпирических знаний экспертов в той или иной проблемной области. База правил системы нечеткого вывода представляет собой конечную совокупность нечетких правил, согласованную относительно используемых в них лингвистических переменных. Наиболее часто база правил представляется в виде структурированного текста:

{Ri}ki=1=		R1: ЕСЛИ А1 ТО B1	()	(4.44)
		R2: ЕСЛИ А2 ТО B2	()
		R3: ЕСЛИ А3 ТО B3	()
		…
		RN: ЕСЛИ АN ТО BN	()

где - коэффициенты определенности или весовые коэффициенты соответствующих правил. В случае, когда весовые коэффициенты отсутствуют, удобно принять, что они равны 1.

В системах нечеткого вывода лингвистические переменные, которые используются в нечетких высказываниях подусловий нечетких правил, часто называют входными лингвистическими переменными. А переменные, которые используются в нечетких высказываниях подзаключений правил нечетких продукций, часто называют выходными лингвистическими переменными.

Таким образом, при формировании базы правил нечетких продукций необходимо определить:

1. Множество правил нечеткой продукции {R_i}^k_i=1 в форме (4.44)

2. Множество выходных лингвистических переменных

3. Множество выходных лингвистических переменных

Для базы правил справедливы следующие свойства:

• непрерывность;

• непротиворечивость;

• полнота.

Для того чтобы определить непрерывность {R_i}^k_i=1, используются сле­дующие понятия:

• упорядоченная совокупность нечетких множеств;

• прилегающие нечеткие множества.

Совокупность нечетких множеств {A_i} называется упорядоченной, если для них задано отношение порядка, например:

“<”: A₁<A₂<…<A_i-1<A_i<A_i+1<…

Если {A_i} упорядочена, тогда множества A_i-1 и A_i, A_i и A_i+1 называ­ются прилегающими. Здесь предполагается, что эти нечеткие множества являются перекрывающимися.

База правил {R_i}^k_i=1 называется непрерывной, если для правил

R_k : если х₁ = A_1k и х₂ = A_2k, тогда y = B_k и k'  k имеем:

• А_1k = А_1k' A_2k и A_2k' являются прилегающими;

• А_2k ⁼ А_2k' A_1k и A_1k' являются прилегающими;

• B_k и B_k' являются прилегающими.

Непротиворечивость базы правил демонстрируем на примерах 4.10 и 4.11.

Пример 4.10. Нечеткое управление роботом.

…

или

R_k: если препятствие впереди, то двигайся влево,

{R_i}ⁿ_i=1 = или

R_k+l: если препятствие впереди, то двигайся вправо,

или

…

База правил {R_i}ⁿ_i=1 противоречива.

Пример 4.11. Нечеткая система (рис.4.4)

R₁: если x_l = А или х₂ = Е, тогда у = Н;

{R_i}³_i=1 = R₂: если x_l = С или х₂ = F, тогда у = I;

R₃: если x_l = В или х₂ = D, тогда у = G .

В терминах управления правила, которые содержат два условия и один вывод, представляют собой систему с двумя входами х₁, х₂ и одним вы­ходом у, В этом случае алгоритм функционирования нечеткой системы может быть задан в матричной форме, как показано на рис.4.4.

x1 x2	A	B	C
D		G	y
E	H
F		I

Рис.4.4. Пример задания функционирования нечеткой системы

Представленная база правил непротиворечива. Пусть теперь база пра­вил имеет вид:

x1 x2	A	B	C
D		G
E	H		H
F		I

Рис.4.5. Противоречивость базы правил

В этом случае база правил противоречива, т.к. она приводит к двусмысленности выводов, как показано в примере 4.10. Этот феномен не так легко может быть идентифицирован, в общем случае, при наличии сложной базы правил.

Полнота {R_i}^k_i=1 используется как мера, указывающая на полноту знаний, которые содержаться в базе правил. Неполная база правил имеет так называемые «пустые места» для определенных ситуаций (на семантиче­ском уровне), т.е. не определены связи между входами и выходами. Это не означает, что результат вывода из правила не существует из-за неполноты базы правил, а этот эффект обусловлен свойствами нечетких множеств, которые используются в условиях правил.

В качестве меры полноты используется критерий:

,

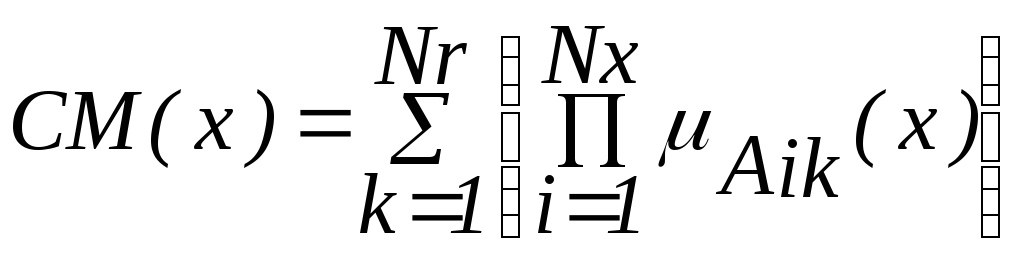(4.45)

где х - физическая переменная входных данных (условий); N_x - число условий в правиле; N_r - число правил в базе правил. Например, при N_x=1, N_r=1, что соответствует наличию одного условия (N_x = 1) базе правил, содержащей одно правило (N_r =1), получим:

.

Если ₁₁(х)= 0 , что соответствует пустому месту, получим СМ(х) = 0 . Численные значения, которые принимает критерий СМ(х), позволяют классифицировать базы правил по полноте знаний:

• СМ(х) = 0 - «неполная» база правил;

• 0 < СМ(х)<1 - база правил «незначительно полная»;

• СМ(х) = 1 - база правил «точно полная»;

• СМ(х)>1 - база правил «сверхполная (избыточная)».

Таким образом, при разработке алгоритмов нечетких систем управле­ния в виде базы правил обязательным этапом анализа алгоритма является проверка соответствующей базы правил на непрерывность, непротиворе­чивость и полноту и далее приступают к компьютерной реализации алго­ритма управления.