
Главы 7-8
.pdfГЛАВА 7. КРИВЫЕ ЛИНИИ
В начертательной геометрии кривую линию можно представить как траекторию непрерывного движения точки в пространстве. Если точка движется по определенному закону, получается закономерная линия – окружность, эллипс, парабола, гипербола, синусоида, винтовая линия и др. Закономерные и незакономерные линии можно подразделить на плоские и пространственные.
Свойства ортогональных проекций кривой линии:
1.Проекцией кривой линии является кривая линия;
2.Касательная к кривой линии проецируется в касательную к еѐ проекции;
3.Несобственная точка кривой проецируется в несобственную точку еѐ проекции;
4.Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше;
5.Число узловых точек (в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.
! Случаи когда, плоская кривая проецируется в прямую (свойства 1,4,5), а касательная в точку (свойство 2) не учитываются.
7.1. ПЛОСКИЕ КРИВЫЕ ЛИНИИ. ПРОЕЦИРОВАНИЕ ОКРУЖНОСТИ
У плоской линии все точки принадлежат одной плоскости (прямая, окружность, эллипс, гипербола и др.). Одной из характеристик линии является так называемый «порядок» линии. В математике порядок определяется степенью уравнения, которым можно задать линию. В геометрии порядок определяется максимальным количеством точек, полученных при пересечении с плоскостью (точки могут быть действительными и мнимыми (бесконечно удаленными)). Прямая линия пересекается с плоскостью в одной точке – значит она первого порядка, окружность, эллипс, парабола, гипербола – второго порядка.
Рассмотрим подробнее проецирование окружности. Проекцией окружности радиусом R в общем случае является эллипс. Большая и малая оси эллипса – проекции двух взаимно перпендикулярных диаметров окружности (рис. 7.1).
Один из них параллелен плоскости проекций, проецируется на нее в натуральную величину АВ=2R и является большой осью эллипса. Другой диаметр является линией наибольшего наклона плоскости окружно-
129

сти и проецируется в малую ось эллипса СD, длиной 2R cos , где – угол наклона плоскости окружности к плоскости проекций.
Для построения эллипса рационально использовать метод концентрических окружностей, который состоит в следующем (рис. 7.1):
1.Строим большую АВ и малую CD оси эллипса.
2.Проводим две окружности n и m диаметрами, равными большой АВ и малой CD осям соответственно.
3.Строим промежуточные точки, принадлежащие эллипсу:
–проводим произвольную прямую l, проходящую через центр О эллипса;
–пересечение прямой l с окружностью n – точка 1, с окружностью m –точка 2;
–проводим перпендикуляр р из точки 1 к большой оси АВ и перпендикуляр р' из точки 2 к малой оси CD;
–пересечение перпендикуляров р и р' дает точку N, принадлежащую эллипсу;
–строим точки М, К, и L, симметричные точке N, относительно большой и малой осей;
–аналогично строим еще несколько промежуточных точек (для более точного построения эллипса). Количество точек должно быть достаточным для обводки по лекалу.
4. Соединяем полученные точки плавной линией (по лекалу).
Рис.7.1. Построение эллипса методом концентрических окружностей
Если окружность принадлежит:
–плоскости уровня, то проекциями окружности на трехкартинном чертеже являются окружность и отрезки;
–проецирующей плоскости, то проекции окружности – отрезок и эллипсы.
130
7.2. ПРОСТРАНСТВЕННЫЕ КРИВЫЕ ЛИНИИ
Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.
Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.
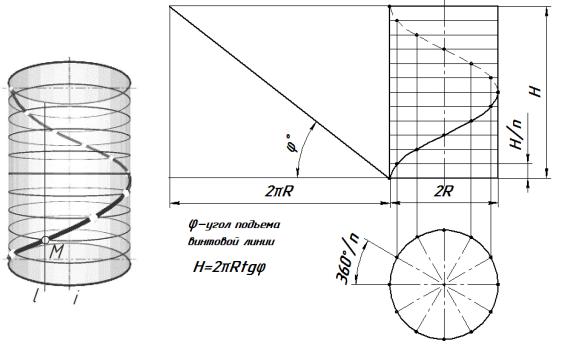
Цилиндрическая винтовая линия. При перемещении в пространстве точка М совершает сложное движение – равномерно движется по образующей l, которая в свою очередь равномерно вращается вокруг оси цилиндра i (рис. 7.2).
Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии. Различают правую и левую винтовые линии.
а) |
б) |
Рис.7.2. Цилиндрическая винтовая линия (правая): а – модель; б – эпюр
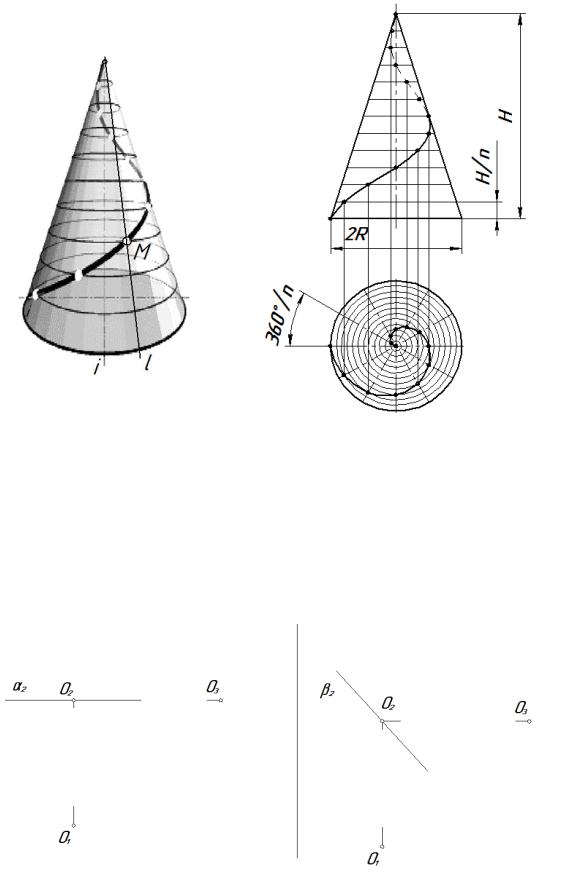
Коническая винтовая линия. Такую линию описывает точка M, которая движется по какой-либо образующей l прямого кругового конуса, вращающегося вокруг своей оси i (рис. 7.3).
Проекция на ось конуса смещения точки вдоль образующей за один оборот называется шагом конической винтовой линии. Горизонтальной проекцией конической винтовой линии является спираль Архимеда – одна из плоских кривых линий.
131
а) |
б) |
Рис.7.3. Коническая винтовая линия: а – модель; б – эпюр
Рассмотрим решение задач по изучаемой теме.
Задача.
Построить проекции окружности с центром в точке О, радиусом 15 мм и принадлежащей плоскости:
Дано:
а) α; |
б) β |
132
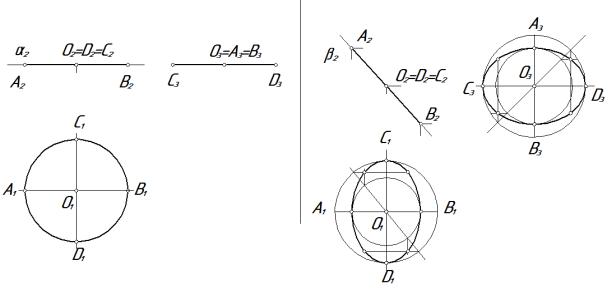
Решение:
а) α; |
б) β |
ГЛАВА 8. ПОВЕРХНОСТИ ВРАЩЕНИЯ
Поверхностью вращения называется поверхность, образованная вращением некоторой линии (образующей) вокруг прямой (оси вращения i) (рис. 8.1). Каждая точка М кривой описывает окружность m, которая называется параллелью. Плоскость параллели перпендикулярна оси вращения поверхности, центр параллели – точка пересечения плоскости параллели с осью вращения поверхности и радиус параллели равен расстоянию от ее центра до точки пересечения плоскости параллели с образующей поверхности.
Параллель наибольшего диаметра называется экватором n, наименьшего – горлом t. Кривая линия, получающаяся от пересечения поверхности вращения плоскостью, проходящей через ось, называется
меридианом l (рис. 8.1).
Рассмотрим понятие контура поверхности. Проводем множество проецирующих прямых рi касательно поверхности вращения Q, получим множество точек касания, которые образуют контур l поверхности (рис. 8.2). При проецировании точек касания на плоскость проекций Пi получим линию li , которая является проекцией контура l .
Аналогично получаются любые контуры поверхности. В общем случае поверхности имеют три основных контура: горизонтальный, фронтальный и профильный, каждый из которых имеет проекции на плоскостях проекций П1, П2 и П3.
133
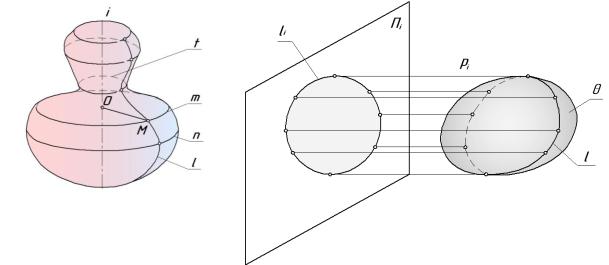
Рис. 8.1. Параллели поверхности |
Рис. 8.2. Контур поверхности |
Для определения недостающих проекций точки, принадлежащей поверхности вращения, используются линии поверхности: контур или параллель.
Определение условной видимости проекций точки производится исходя из ее расположения на поверхности. Границу видимости определяет соответствующий контур поверхности.
8.1. КОНТУРЫ И ТОЧКИ НА ПОВЕРХНОСТИ. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ
Рассмотрим основные поверхности вращения, часто встречающиеся в технике.
8.1.1. СФЕРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ
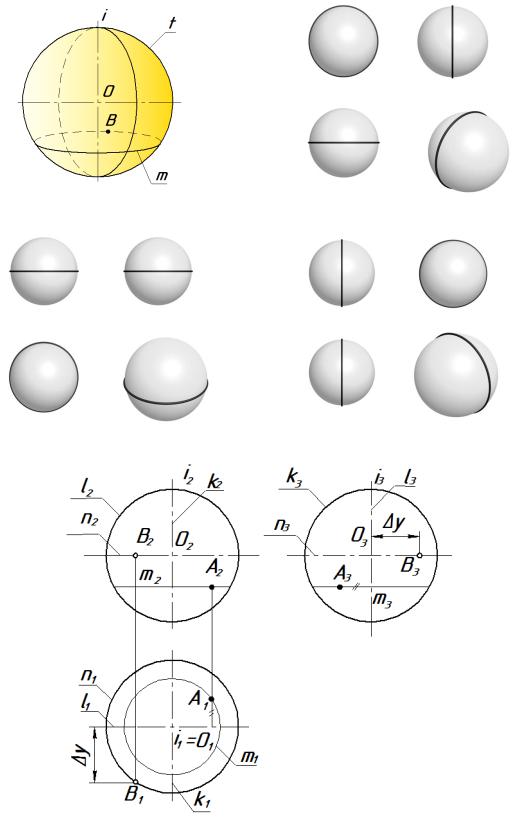
Сферическая поверхность образуется вращением окружности t вокруг оси i, принадлежащей плоскости этой окружности и проходящей через ее центр О (рис. 8.3 а). Осью вращения сферы может быть любая прямая, проходящая через ее центр. Поэтому сфера на чертеже определяется положением ее центра. Фронтальным контуром сферы является окружность l, профильным – окружность k, горизонтальным контуром – окружность n (рис. 8.3 б, в, г, д).
Рассмотрим построение недостающих проекций точек А и В и определение их видимости.
134
а) |
б) |
в) |
г) |
д)
Рис.8.3. Сферическая поверхность: а – модель; б – фронтальный контур; в – горизонтальный контур; г – профильный контур; д – трехкартинный чертеж
135
На чертеже заданы невидимая фронтальная проекция А2 точки А и видимая фронтальная проекция В2 точки В. Обозначение видимости: видимые точки не закрашиваются, невидимые точки – закрашиваются.
Недостающие проекции точки А на поверхности сферы определяются по принадлежности к параллели m.
Фронтальная проекция В2 точки В принадлежит фронтальной проекции n2 горизонтального контура n. Следовательно, точка В принадлежит горизонтальному контуру n поверхности сферы. Построение недостающих проекций точки В выполняется по принадлежности их к соответствующим проекциям данного контура.
Видимость проекций точек A (A1, А3) и В (В1, В3) на плоскостях проекций определяется исходя из их расположения относительно соответствующих контуров поверхности.
В табл. 8.1 приведены схемы определения видимости точек на плоскостях проекций. Например, для определения видимости на плоскости П1 , необходимо смотреть сверху на проекции на плоскостях П2 , П3 и ориентироваться по горизонтальному контуру. Все точки, которые находятся выше горизонтального контура (в видимой части) – видимы на плоскости П1, которые ниже (в невидимой части) – невидимы на плоскости П1.
8.1.2. КОНИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ
Конус вращения образуется вращением прямой (образующей t) вокруг пересекающейся с ней оси i в точке S (рис.8.4, а).
На трехкартинном чертеже (рис. 8.4, б) ось i перпендикулярна плоскости П1. Фронтальный контур конической поверхности представляет собой две пересекающиеся прямые l и l', профильный контур – две пересекающиеся прямые k и k'.
Коническая поверхность безгранична вдоль оси, поэтому горизонтальный контур отсутствует.
Как правило, в конической поверхности берется одна часть (в ту или иную сторону от вершины S), кроме того, вводится плоскость ограничения α, перпендикулярная оси вращения и ограничивающая коническую поверхность. Линия пересечения этой плоскости с конической поверхностью называется линией ограничения n.
136

Таблица 8.1. Схемы определения видимости
Модель |
|
Схема - комплексный чертеж |
|
|
|
|
Определение видимости на П1 |
|
|
|
|
Определение видимости на П2
Определение видимости на П3
137

Рассмотрим построение недостающих проекций точек А и В, принадлежащих конической поверхности, а также определение их видимости (рис. 8.4, б).
На чертеже заданы видимая фронтальная проекция А2 точки А и видимая горизонтальная проекция В1 точки В.
Для определения недостающих проекций точки А используется параллель m, которой принадлежит точка А. Параллель проецируются на плоскость П1 без искажения (в виде окружности), на плоскостях П2 и П3
– в виде отрезка прямой, перпендикулярной оси проекций, длиной, равной диаметру параллели. Недостающие проекции точки A (A1 и А3) находятся по принадлежности к параллели m. На плоскости П1 горизонтальная проекция А1 строится в видимой части (ниже горизонтальной проекции фронтального контура конуса), так как фронтальная проекция А2 точки А видимая. Проекция точки А на плоскости проекций П3 (профильная проекция А3) видима, т.к. проекция А2 расположена в видимой части (левее профильного контура конической поверхности).
Горизонтальная проекция В1 принадлежит горизонтальной проекции фронтального контура l'1, следовательно, точка В расположена на фронтальном контуре l' поверхности конуса. Построение недостающих проекций точки В производится по принадлежности их к соответствующим проекциям данного контура. Точка В принадлежит фронтальному контуру, следовательно, она расположена на границе видимости, поэтому ее проекция В2 считается видимой на фронтальной плоскости проекций П2. Точка В2 расположена в невидимой части (правее профильного контура), следовательно, ее проекция В3 на профильной плоскости проекций П3 – невидимая. Горизонтальные проекции всех точек, принадлежащих поверхности конуса при данном ограничении поверхности, видимы.
а)
Рис.8.4. Коническая поверхность (начало): а – модель;
138
