Методические указания

ПО

Лиенйной алгебре и аналитической геометрии

Тема 1. Линейные пространства и линейные преобразования Задания уровня а

1. Докажите, что множество M с заданными операциями сложения и умножения на число является или не является линейным пространством. Если в конкретном задании не указаны операции, то это – обычные операции сложения и умножения на число на заданном множестве. Если операции отличаются от обычных, то означает операцию сложения, а означает операцию умножения на число. При описании таких операций знаки и означают обычные операции сложения и умножения.

2. Докажите, что система векторов 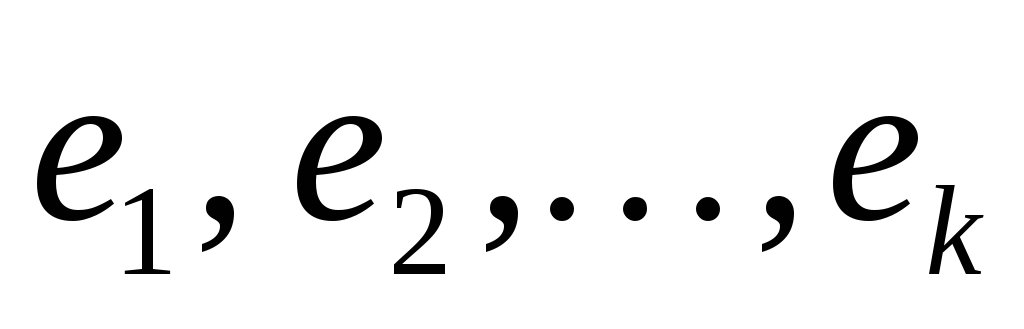пространства L образует базис и найдите координаты вектора в этом базисе.

3. Докажите, что подмножество M линейного пространства L является или не является линейным подпространством.

4. Найдите матрицу линейного преобразования A линейного пространства L в базисе .

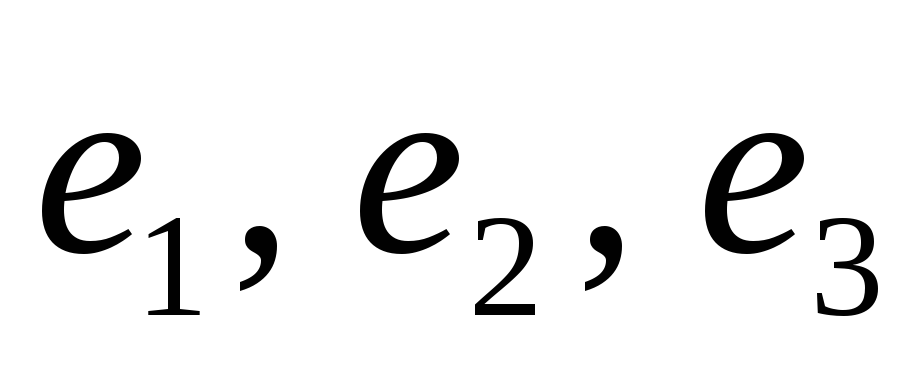5. Задана матрица линейного преобразования A трехмерного пространства в некотором базисе 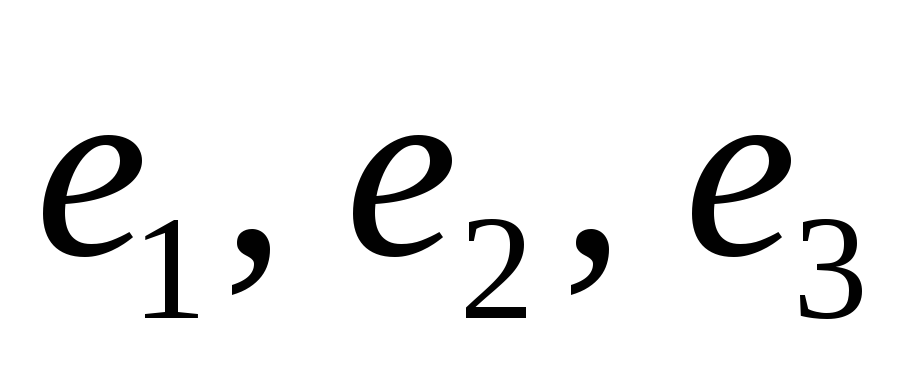. Найдите координаты в этом базисе векторов 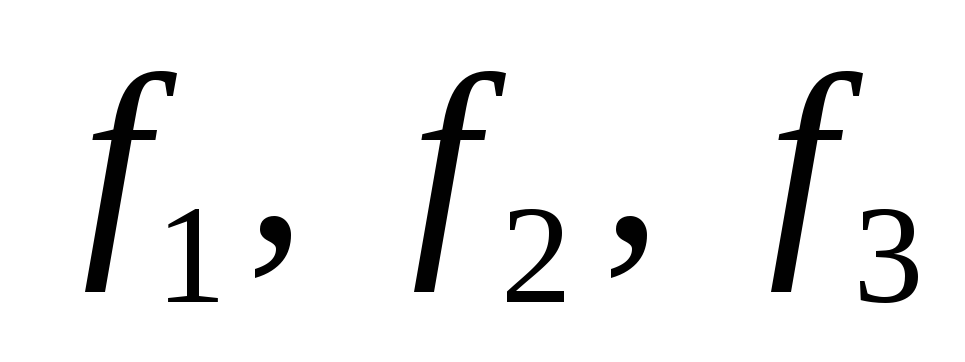, образующих базис, в котором линейное преобразование имеет диагональную матрицу.

Задания уровня в

1. Определить размерность линейного пространства L.

2. Найти базис линейного подпространства 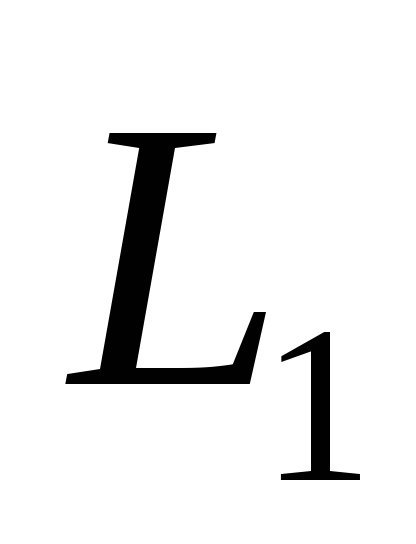линейного пространства L.

3. В линейном пространстве L выбран базис 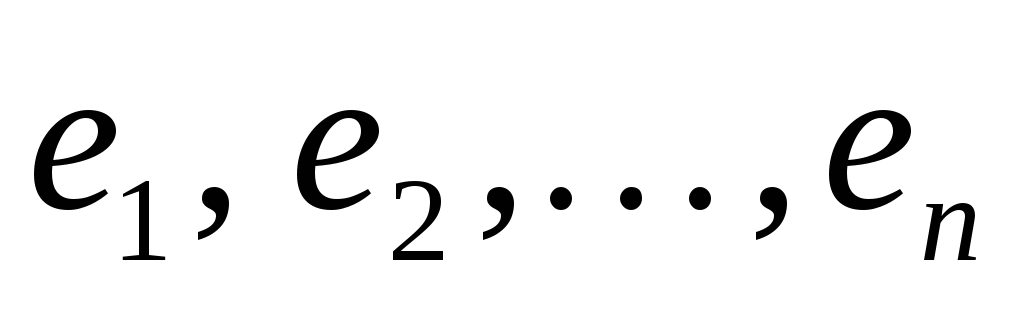. Написать систему линейных уравнений, задающих подпространство, являющееся линейной оболочкой векторов .

4. В линейном пространстве L выбран базис 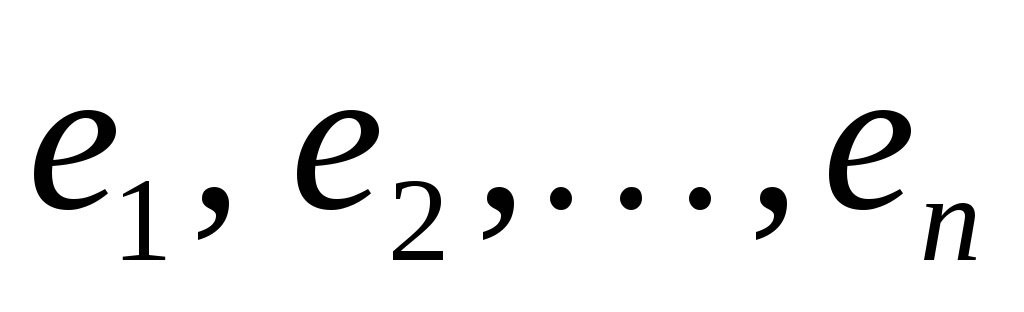. Два его подпространства 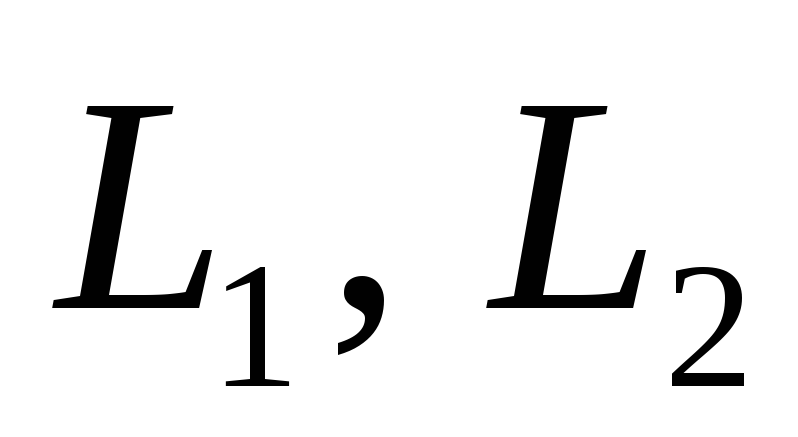заданы системами линейных уравнений. Наибольший из индексов неизвестных равен размерности L. Задать системой линейных уравнений подпространство .

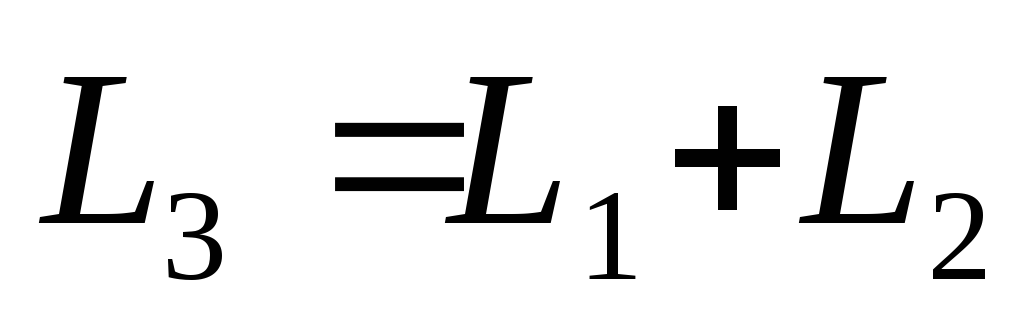5. Выяснить, является ли матрица подобной диагональной матрице 1) над полем вещественных чисел, 2) над полем комплексных чисел.

Условия заданий по теме 1

Вариант 1А

1. М – множество многочленов 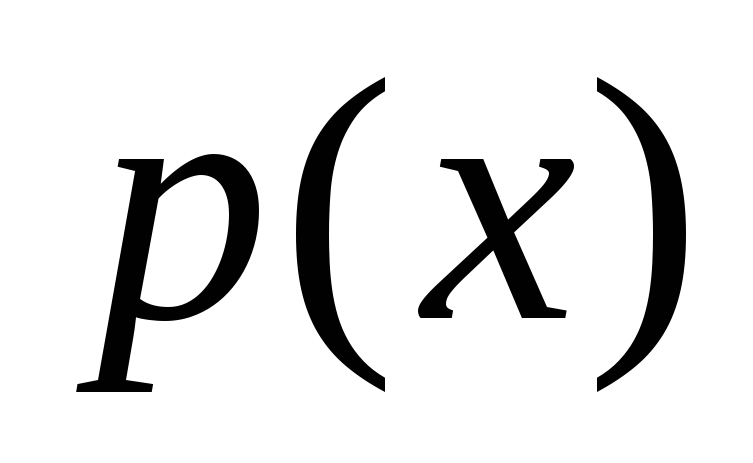, обращающихся в ноль в точке .

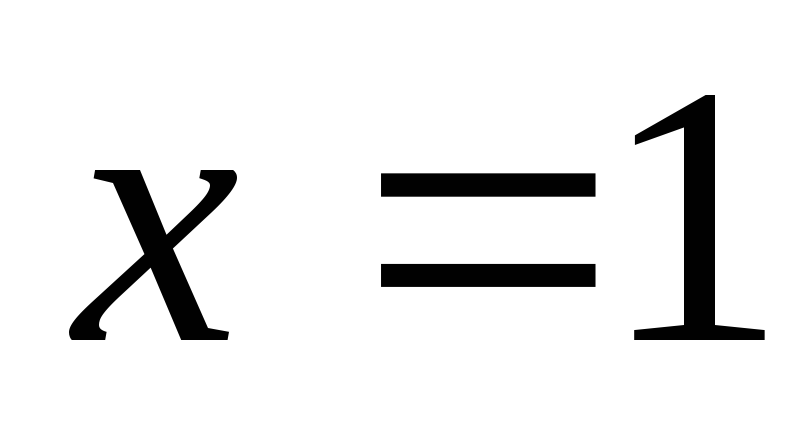2. L – множество матриц второго порядка, , , , , .

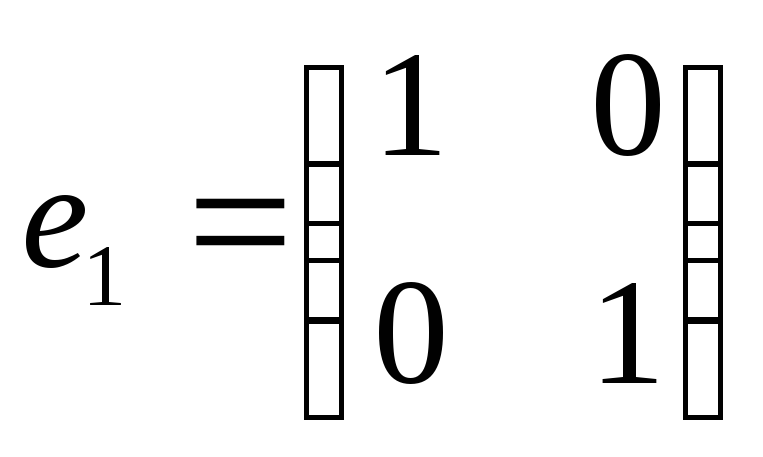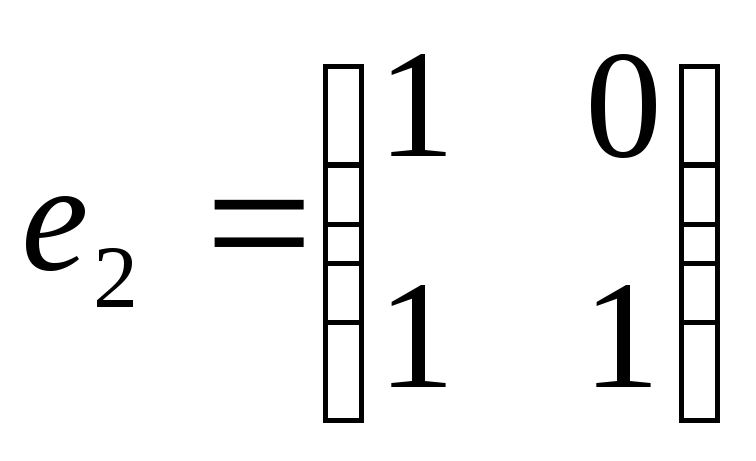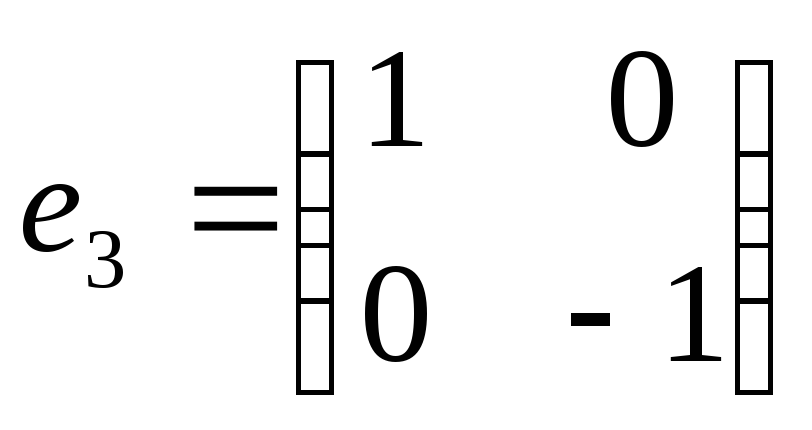3. L – множество матриц-столбцов из четырех элементов, М – множество столбцов, у которых первый элемент равен 1.

4. L – множество матриц второго порядка, 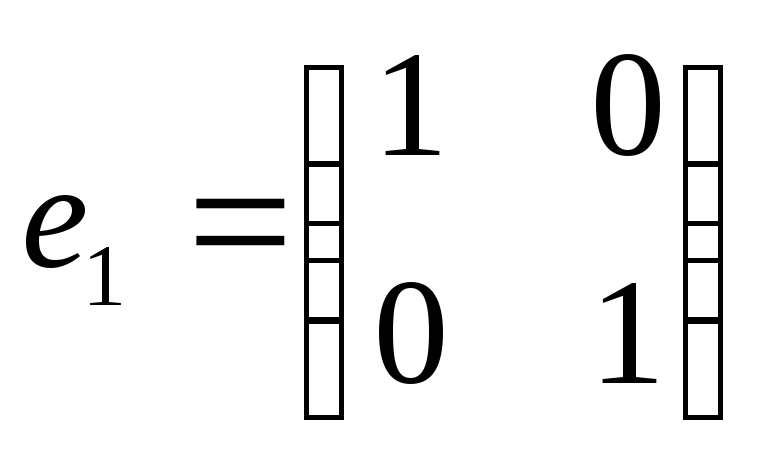, , 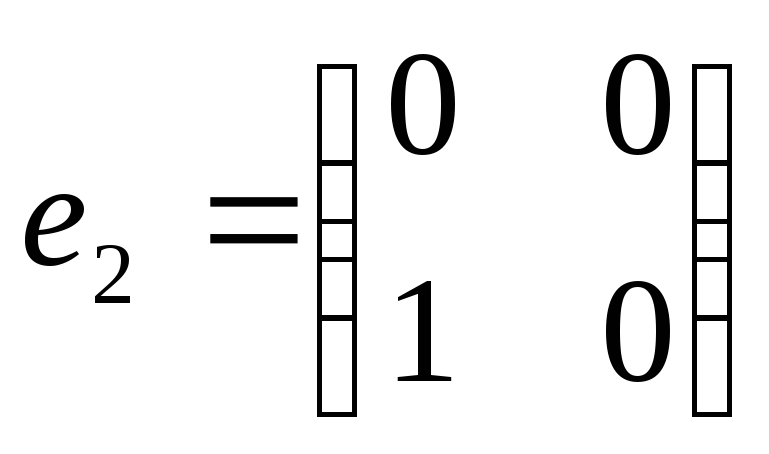, , 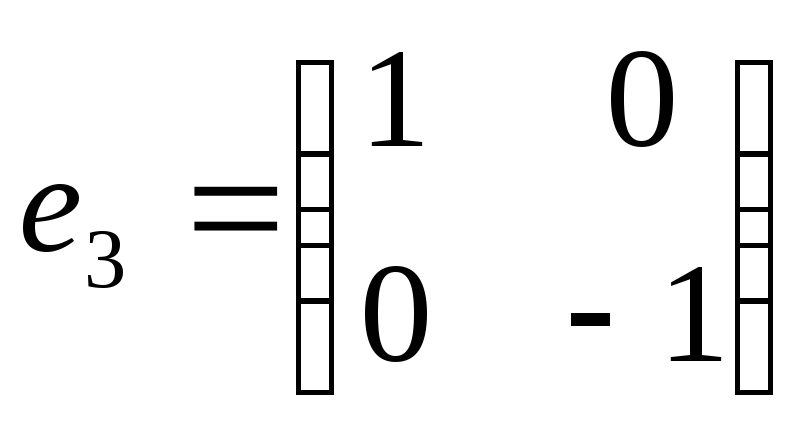A – операция транспонирования.

5. .

Вариант 1В

1. L – линейное пространство, образованное многочленами степени не выше 5, которые обращаются в ноль при 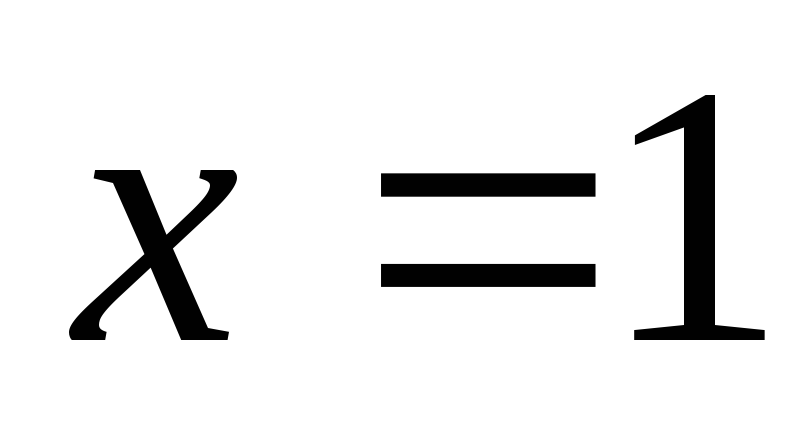и .

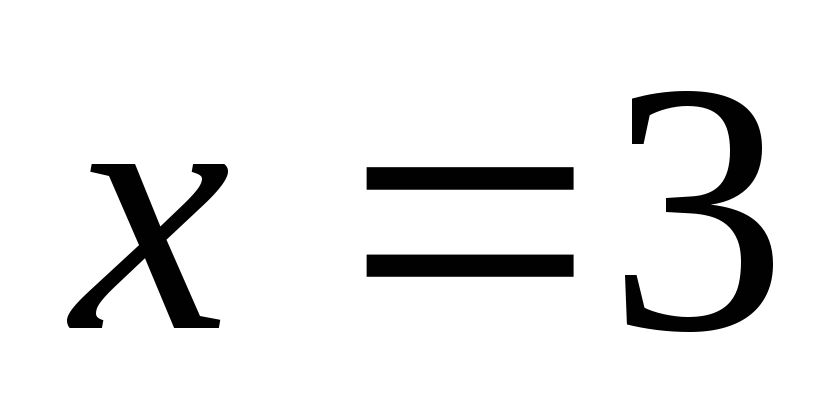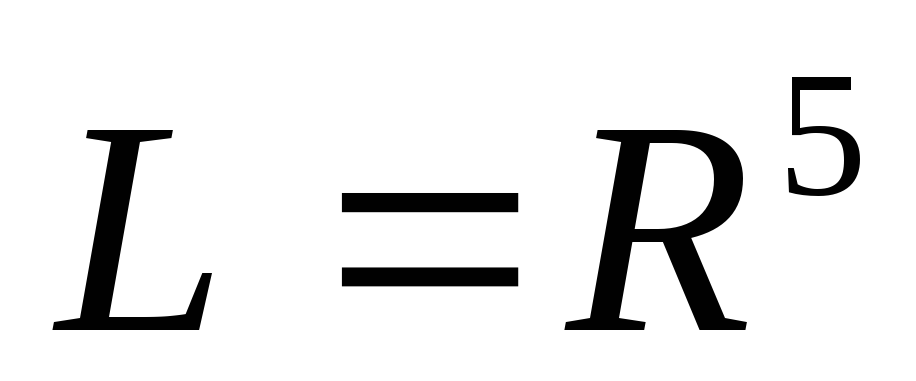2. , в некотором базисе 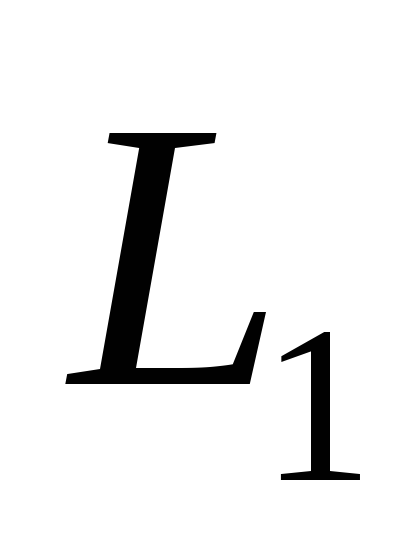задается системой уравнений

3. , , , .

4. 

5. .

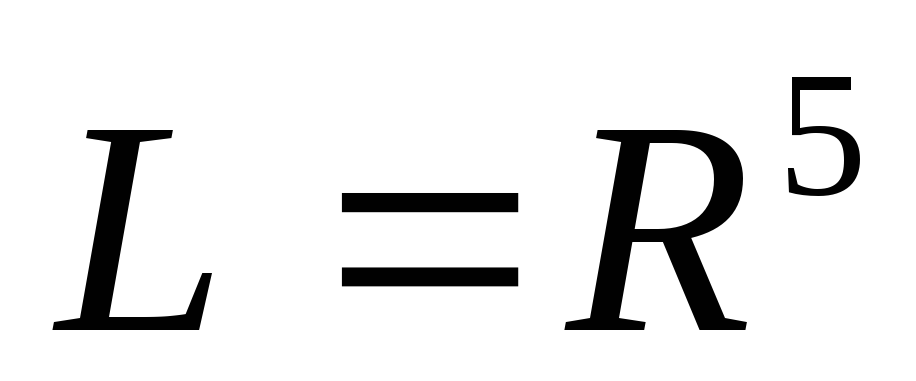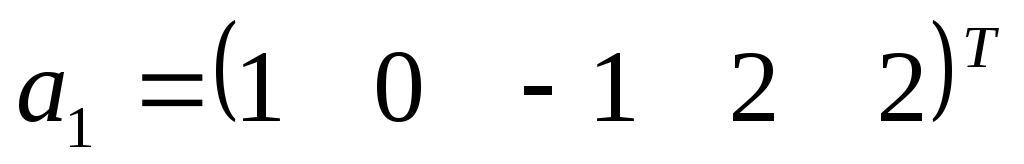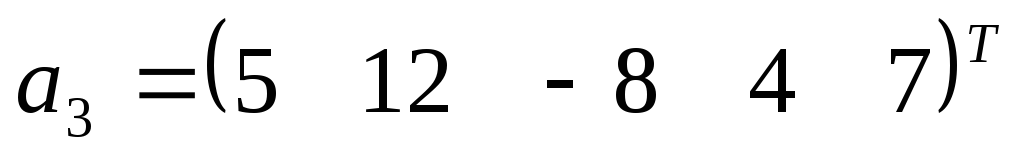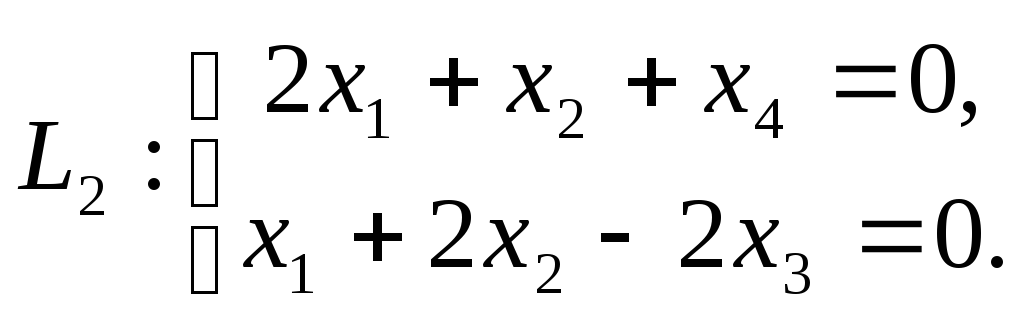
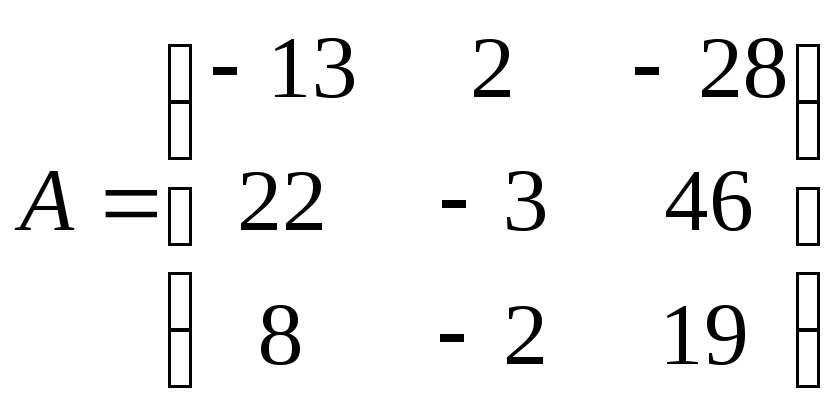Вариант 2А

1. М – множество квадратных матриц порядка 2, у которых сумма диагональных элементов (след матрицы) равна нулю.

2. L – множество многочленов не выше второй степени, , , , .

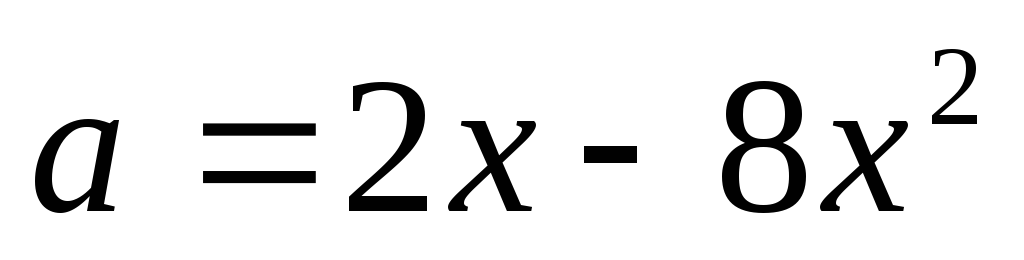3. L – множество матриц-столбцов из четырех элементов, М – множество столбцов, у которых первый элемент равен третьему элементу.

4. L – множество многочленов не выше второй степени, , , , .

5. .

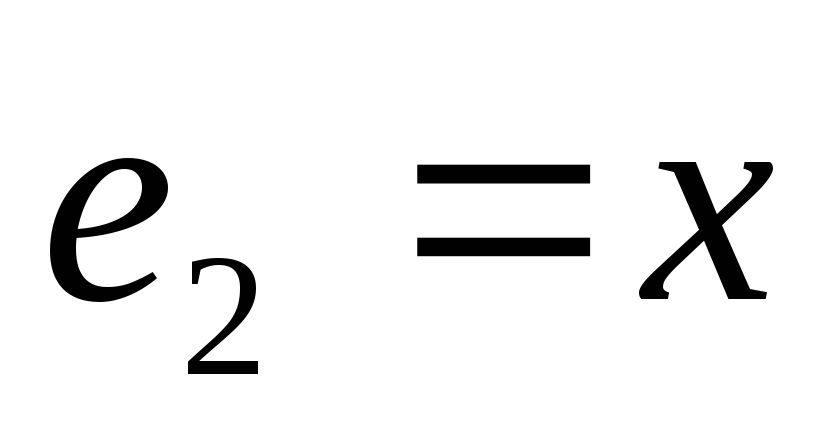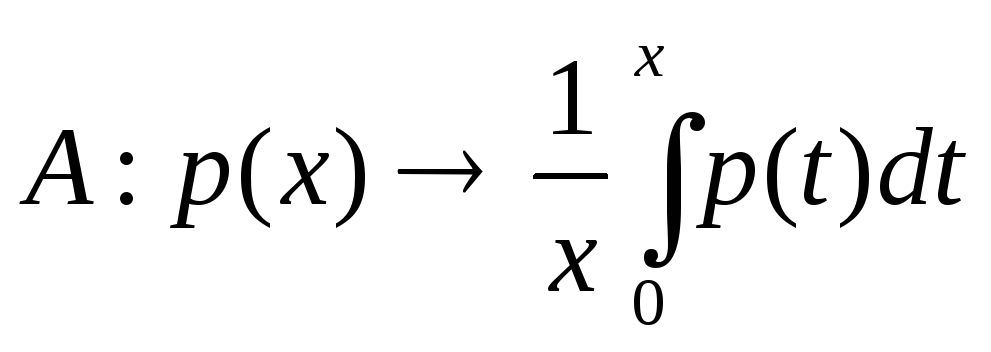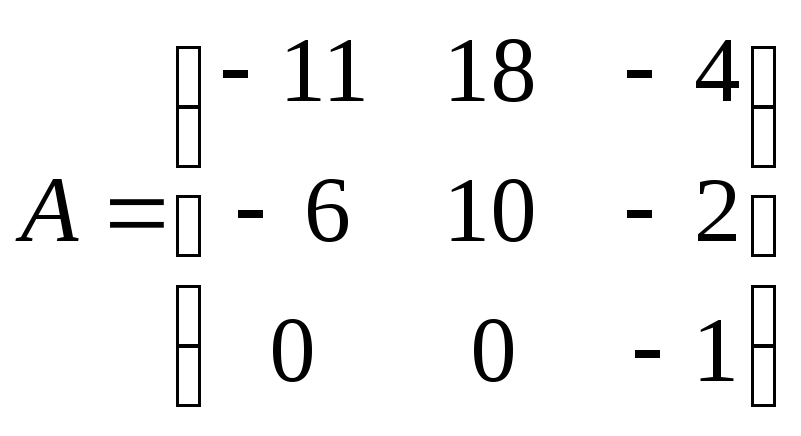Вариант 2В

1. L – линейное пространство матриц третьего порядка, у которых на главной диагонали стоят нули.

2. L – линейное пространство, образованное многочленами степени не выше 4, 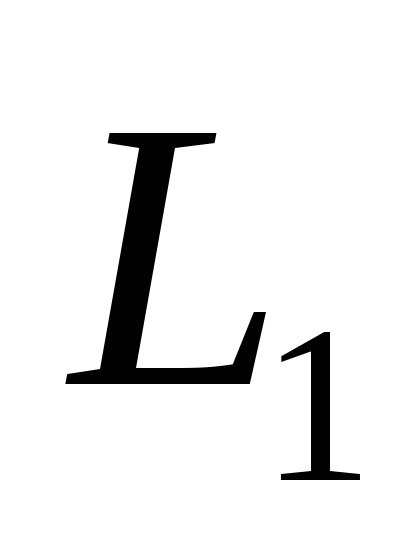–подпространство многочленов, имеющих 1 корнем кратности 2 или выше.

3. , , , .

4. 

5. .

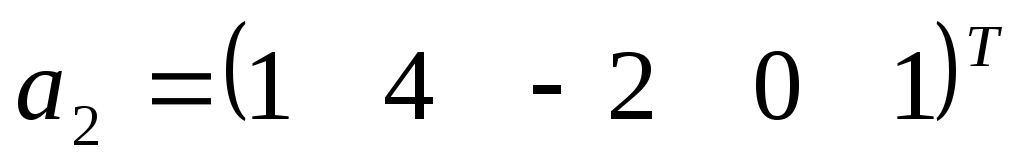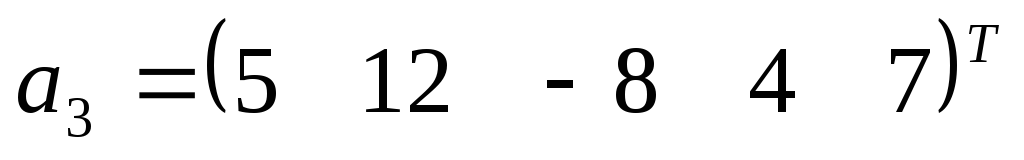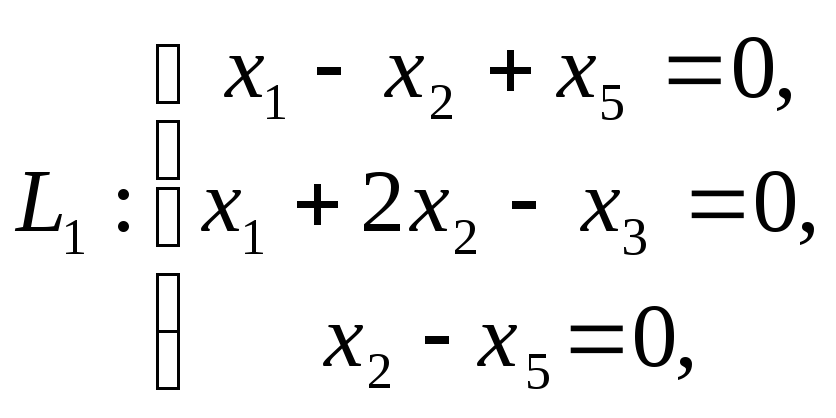
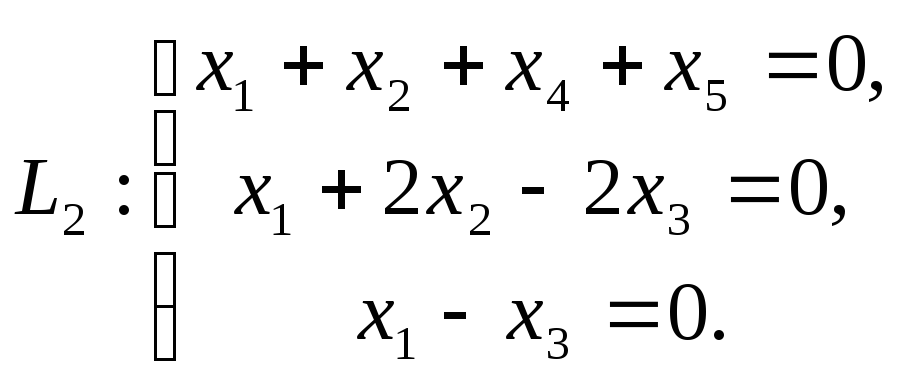
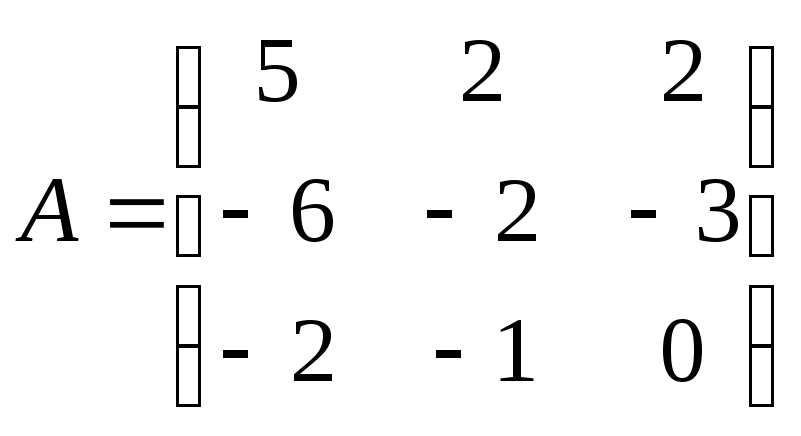Вариант 3А

1. М – множество многочленов степени не выше 5, у которых хотя бы один коэффициент равен нулю.

2. L – множество верхних треугольных матриц порядка 2, , , , .

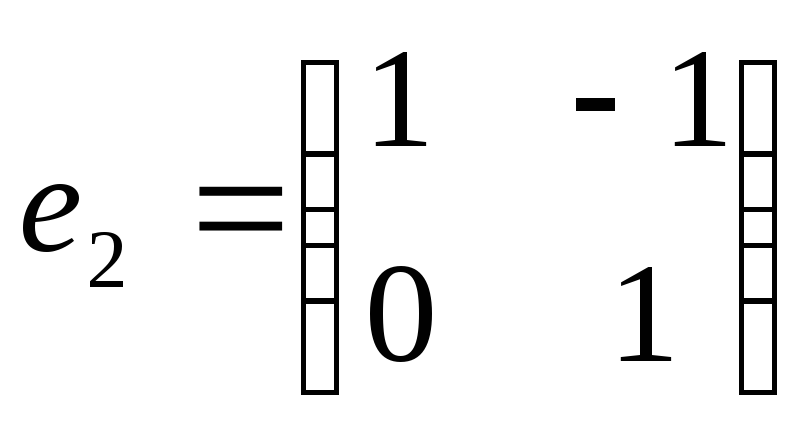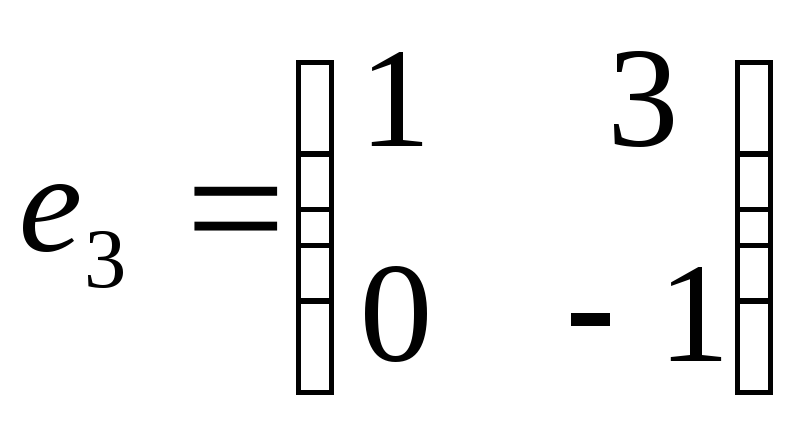3. L – множество матриц-столбцов из четырех элементов, М – множество столбцов, у которых первый элемент равен удвоенному четвертому элементу.

4. L – множество векторов трехмерного пространства, базис – векторы , преобразование A отображает радиус-вектор в радиус вектор симметричный относительно плоскости .

5. .

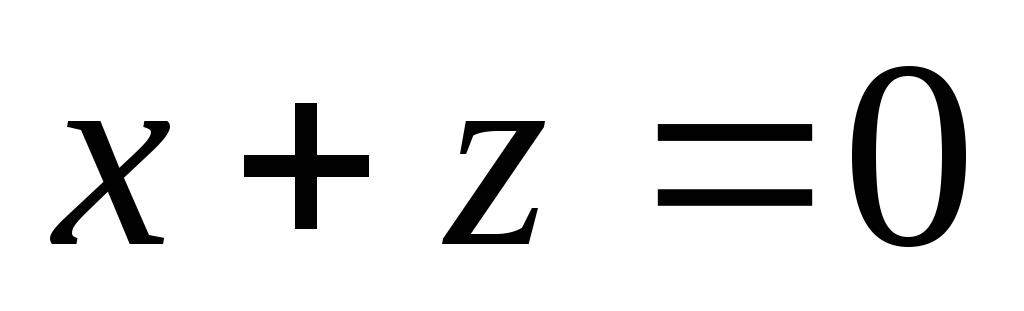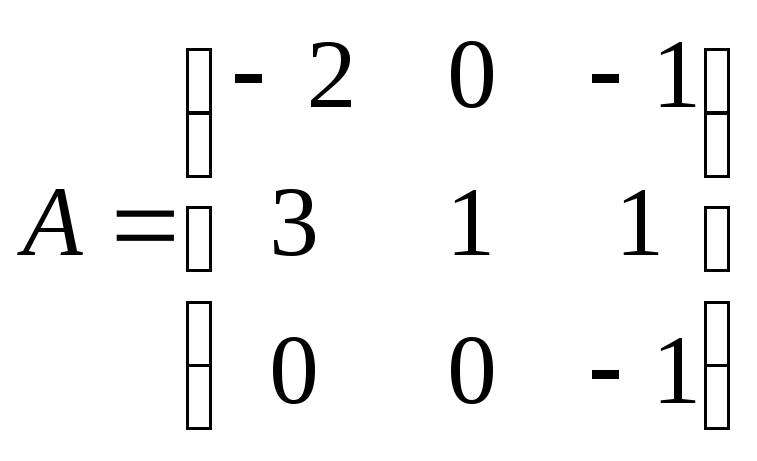Вариант 3В