IV. Скалярное произведение векторов.

Скалярным произведением векторов иназывается число, равное, где- угол между векторами. Это произведение обозначают разными способами

.

Отметим свойства введенного скалярного произведения.

1) (симметричность);

2) (линейность);

3) , причемтогда и только тогда, когда.

Векторное пространство с таким скалярным произведением называется евклидовым пространством. В этом пространстве можно ввести норму (длину) вектора правилом . Для евклидового пространства справедливы следующие теоремы.

Для любых двух векторов иевклидового пространства справедливонеравенство Коши-Буняковского

.

Для любых двух векторов иевклидового пространства с нормой векторасправедливонеравенство треугольника

.

Неравенство Коши-Буняковского позволяет ввести понятие угла между векторами в евклидовом пространстве, для которого

.

Два вектора иназываютсяортогональными, если . В евклидовом пространстве угол между такими векторами равен. Попарно ортогональны орты координатных осей. Поскольку длины этих векторов считаются равными единице (например,), базис, состоящий из подобных векторов, называетсяортонормированным базисом. Учитывая единичную нормировку таких базисных векторов и их попарную ортогональность, легко показать, что

и

.

Пусть материальная точка перемещается прямолинейно из точки в точкупод действием постоянной силы, образующей уголс вектором.

Работа этой силы при перемещении точки на расстояние равна произведению проекции этой силы на направление перемещения на величину перемещения:. Таким образом, скалярное произведение векторовиравно работе силыпри перемещении точки на вектор, т.е.

.

Эта формула отражает физическое приложение скалярного произведения. V. Векторное произведение векторов.

Рассмотрим два вектора и.Векторным произведением этих векторов называется вектор ,

1. равный по величине 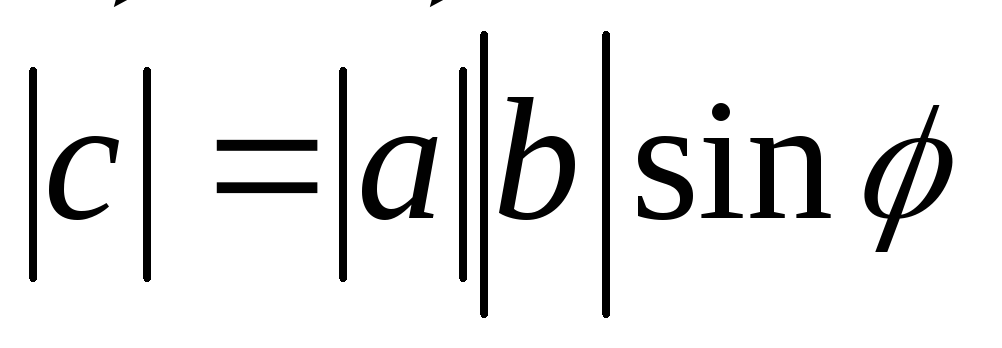, где- угол между векторамии, и

2. имеющий направление, определяемое правилом буравчика, ручка которого вращается от вектора к вектору(т.е. векторперпендикулярен как вектору, так и вектору).

Отметим основные свойства векторного произведения.

1. (антисимметричность).

2. (линейность).

К геометрическим свойствам векторного произведения относят определение коллинеарности векторов и нахождение площади параллелограмма (треугольника).

1. Если векторное произведение векторов иравно нулю, то эти векторыколлинеарны (и наоборот).

2. Площадь параллелограмма, построенного на векторах и, равна длине их векторного произведения:, а площадь соответствующего треугольника - половине его длины:.

В качестве физических приложений можно привести:

1) момент силы относительно точки ;

2) момент импульса относительно точки ;

3) линейная скорость вращения .

Используя свойство линейности векторного произведения и учитывая, что , несложно получить формулу векторного произведения через координаты векторов

.

VI. Смешанное произведение векторов.

Смешанным произведением векторов называют произведение вида

,

т.е. смешанное произведение векторов является числом (скаляром).

Отметим основные свойства смешанного произведения векторов.

1. Смешанное произведение векторов не меняется при их циклической перестановке

.

2. Смешанное произведение векторов не меняется при перемене местами знаков векторного и скалярного умножения

.

Последнее свойство позволяет записывать смешанное произведение в виде (без знаков векторного и скалярного произведений).

3. Смешанное произведение меняет знак при перестановке любых двух векторов, входящих в смешанное произведение, например, .

Используя определение смешанного произведения векторов, не составляет труда получить формулу

,

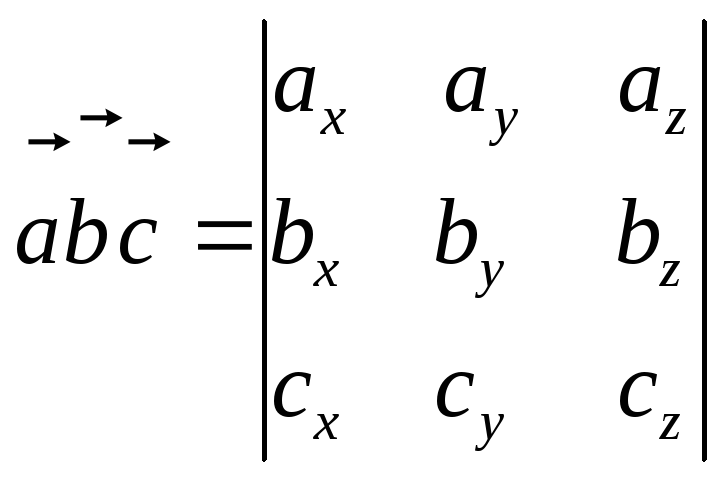позволяющую вычислить это произведение через координаты векторов.

Перечислим основные геометрические приложения смешанного произведение векторов.

1. Определение взаимной ориентации векторов в пространстве.

Если , то векторыиобразуют правую тройку (буравчик двигается в направлении вектора, если его ручка поворачивается от векторак вектору). Если же, то векторыиобразуют левую тройку векторов.

2. Установление компланарности векторов.

Ненулевые векторы икомпланарны тогда и только тогда, когда их смешанное произведение равно нулю:

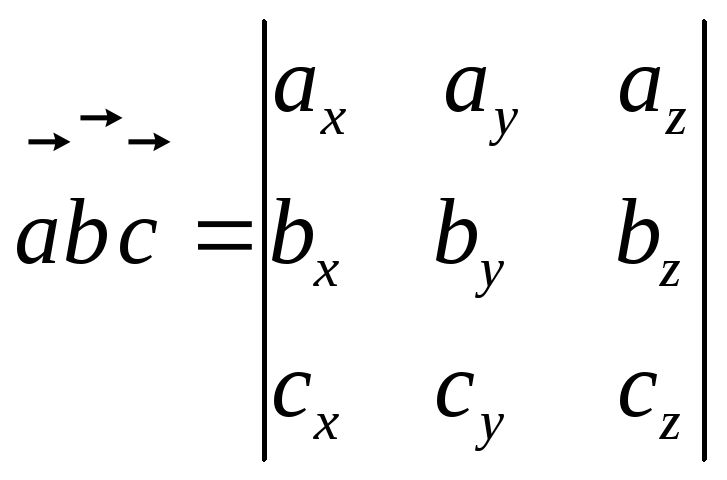=0.

3. Определение объема параллелепипеда.

Объем параллелепипеда, построенного на векторах и, равен модулю их смешанного произведения, т.е..

4. Определение объема треугольной пирамиды.

Объем треугольной пирамиды, построенной на векторах и, равен.

VII. Символ Кронекера и символ Леви-Чивита.

При вычислении различных произведений векторов удобно использовать символы, сокращающие объем вычислений. К таким символам относятся символ Кронекера и символ Леви-Чивита. Символ Кронекера обозначается и определяется следующим образом

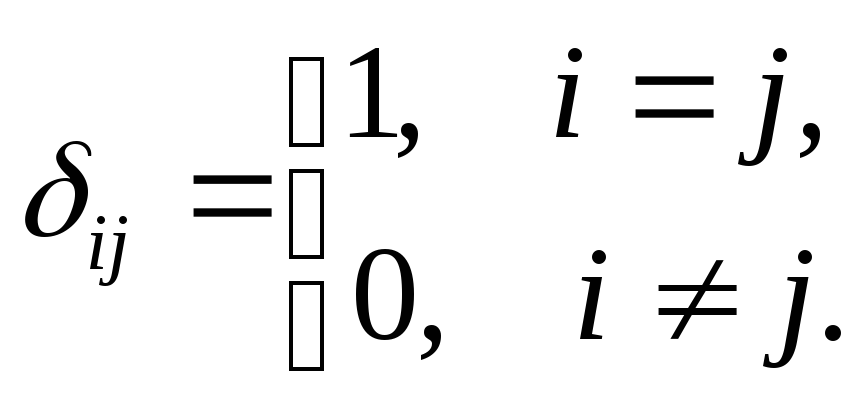
Так если ввести новые обозначения для базисных векторов , то условие ортонормированности базиса запишется в виде

.

Если к этому переобозначить компоненты вектора , то разложение вектора по базису примет вид

.

Можно и эту запись упростить, если договорится, что по повторяющимся индексам подразумевается суммирование (если это не противоречит сути формулы)

.

В новых обозначениях скалярное произведение векторов запишется в виде

.

Заметим, что в силу своего определения символ Кронекера «снимает» сумму, например, .

Символ Леви-Чивита имеет три индекса и обозначается через , при этом полагается, по определению, что. Этот символ является полностью антисимметричным, т.е. при перестановке местами любых двух индексов он меняет знак, например,. Используя это свойство, можно найти значения этого символа при любых индексах, не равных друг другу (). Условие антисимметричности символа Леви-Чивита также приводит к результату: если какие-либо два индекса равны у этого символа, то он равен нулю, например,.

С помощью символа Леви-Чивита -ая координата векторного произведения векторовипредставима в виде

,

где, как говорилось выше, по индексам иберется двойная сумма. Например,

, т.е. .

Смешанное произведение векторов вычисляется по формуле

.

Заметим, что повторяющиеся индексы, по которым проводится суммирование, называются связанными индексами, а индексы, по которым не проводится суммирование, - свободными индексами. В начале расчета и в его конце свободные индексы должны совпадать. При вычислениях полезны формулы

,

.

Если встречается двойная сумма , где объектсимметричный по индексам, а объектантисимметричный, то указанная выше сумма равна нулю. Рассмотрим пример расчета с помощью введенных символов.

Пример. Показать, что .

.

Замечание. Определитель третьего порядка также можно записать через символ Леви-Чивита

.

ЗАДАЧИ